-
Notifications
You must be signed in to change notification settings - Fork 117
Passive Scalars
A passive scalar is a quantity that is transported by the fluid but does not alter the fluid's behavior such as a tracer dye. Athena++ is capable of solving the following equation (in conservation form) for the evolution of any number of passive scalar species i:

where
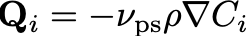
is the diffusive flux density of the i-th species, controlled by the passive scalar diffusion coefficient νps (which must be equal for all species at this time).
In relativity, the evolution equation is ∂0 ((-g)1/2Ci ρu 0) + ∂j ((-g)1/2Ci ρu j) = 0. Diffusion should not be applied to relativity.
Similar to the hydrodynamic variables, our approach to solving this governing equation requires maintaining a dual representation of the cell-centered passive scalar fields. These representations are stored in 4D AthenaArray memory registers within the PassiveScalars object member of each MeshBlock.
-
Conservative variables: the densities of each species = D Ci, where D is the conserved density. Stored in
PassiveScalars::s. -
Primitive variables: the density-normalized, dimensionless fractions (also known as "concentrations") of each species = Ci in [0, 1]. Stored in
PassiveScalars::r.
Variable floors are applied to these quantities during interface reconstruction and equation of state conversions to ensure that 1) the primitive r remains in [0, 1] and 2) the conservative s is consistent with r and the fluid density. The default value of the floor is ~3e-18. The user can set the value of the floor in the input file sfloor=[value] in the block.
Note: many applications (multimaterials, chemistry networks, etc.) may require that the sum of all concentrations Ci = 1 exactly everywhere in the domain for the lifetime of the simulation. Athena++ currently does not perform a renormalization step to ensure this constraint.
To configure the code to evolve one or more species of passive scalars, run the configure.py script with --nscalars=N. This will set the internal preprocessor macro NSCALARS to N. See the Configuring page for more details.
As mentioned within the Problem Generators page, if NSCALARS > 0, the required implementation of void MeshBlock::ProblemGenerator(ParameterInput *pin) must initialize the conservative formulation AthenaArray<Real> PassiveScalar::s of each type of passive scalar on every MeshBlock. The following code is an example created by modifying the function in src/pgen/slotted_cylinder.cpp:
void MeshBlock::ProblemGenerator(ParameterInput *pin) {
AthenaArray<Real> vol(ncells1);
Real d0 = 1.0; // uniform fluid density across the mesh
// initialize conserved variables
for (int k=ks; k<=ke; k++) {
for (int j=js; j<=je; j++) {
pcoord->CellVolume(k, j, is, ie, vol);
for (int i=is; i<=ie; i++) {
// uniformly fill all scalars to have equal concentration
constexpr int scalar_norm = NSCALARS > 0 ? NSCALARS : 1.0;
if (NSCALARS > 0) {
for (int n=0; n<NSCALARS; ++n) {
pscalars->s(n,k,j,i) = d0*1.0/scalar_norm;
}
// ... initialize Hydro conserved variables
}
}
}
}Another simple example of this initialization is provided in src/pgen/shock_tube.cpp.
- Passive scalars are automatically compatible with all of the built-in Boundary Conditions and their associated flags. As with the hydrodynamic variables, the boundary conditions are applied to the cell-centered primitive passive scalar quantities (dimensionless concentrations) and the conservative passive scalar variables (specieis densities) are automatically calculated from those updated values. However, User-Defined Boundary Conditions are currently unsupported for
NSCALARS > 0since there is noAthenaArra<Real> &rparameter in the function signature. We are planning on extending this feature soon. - When
NSCALARS > 0, the Outputs that specify eitherconsorprimvariables will automatically include the conservative or primitive formulation of each passive scalar species, respectively. Restart Files for simulations with passive scalars automatically contain the conservedsdata across the mesh. - Passive scalars are compatible with special and general relativity.
- The treatment of passive scalars is also compatible with both Static Mesh Refinement (SMR) and Adaptive Mesh Refinement (AMR). For AMR, the user-provided
int RefinementCondition(MeshBlock *pmb)function may be written to depend on the passive scalar variables stored withinpmb->pscalars. - Passive scalars can be modified via the user-enrolled explicit hydro source function; see below.
-
Diffusion Processes are also supported for the passive scalars, and can be activated by setting a positive
problem/nu_scalar_isovalue in The Input File or when Overriding Input Parameters.
> make clean; ./configure.py --prob=slotted_cylinder --eos=isothermal --nscalars=1 --nghost=4 -mpi -hdf5; make -j
> cd bin
> mpirun -n 8 ./athena -i ../inputs/hydro/athinput.slotted_cylinder2d_refined mesh/nx1=100 mesh/nx2=100 mesh/refinement=adaptive time/xorder=3 time/integrator=rk3
Figure 1: plot of the passive counter-clockwise advection of a 2D slotted cylinder scalar profile at t=0.4 using RK3+PPM with AMR.

Figure 2: same result as shown in Figure 1 but zoomed-in near the sharp discontinuities around the slot. The gas velocity vector field is overlaid in a constant color.

The following function can be enrolled via EnrollUserExplicitSourceFunction (in Newtonian hydrodynamics, configured with at least 1 passive scalar) to trace how much a given cell has been affected by any material with a temperature above 5. Any cell with a temperature above the threshold has its conserved scalar set to match the conserved density (i.e., its primitive concentration is set to 1, but indirectly via conserved quantities). This scalar is then advected with the flow, so that the primitive concentration at any time corresponds to the fraction of mass that has been at a temperature above the threshold.
void Tracer(MeshBlock *pmb, const Real time, const Real dt, const AthenaArray<Real> &prim,
const AthenaArray<Real> &prim_scalar, const AthenaArray<Real> &bcc,
AthenaArray<Real> &cons, AthenaArray<Real> &cons_scalar) {
Real gamma = pmb->peos->GetGamma();
int is = pmb->is;
int ie = pmb->ie;
int js = pmb->js;
int je = pmb->je;
int ks = pmb->ks;
int ke = pmb->ke;
for (int k = ks; k <= ke; ++k) {
for (int j = js; j <= je; ++j) {
for (int i = is; i <= ie; ++i) {
Real dd = cons(IDN,k,j,i);
Real ee = cons(IEN,k,j,i);
Real mm1 = cons(IM1,k,j,i);
Real mm2 = cons(IM2,k,j,i);
Real mm3 = cons(IM3,k,j,i);
Real rho = dd;
Real mm_sq = SQR(mm1) + SQR(mm2) + SQR(mm3);
Real ee_kinetic = mm_sq / (2.0 * rho);
Real ee_internal = ee - ee_kinetic;
Real p = (gamma - 1.0) * ee_internal;
Real tt = p / rho;
if (tt > 5.0) {
cons_scalar(0,k,j,i) = dd;
}
}
}
}
return;
}Getting Started
User Guide
- Configuring
- Compiling
- The Input File
- Problem Generators
- Boundary Conditions
- Coordinate Systems and Meshes
- Running the Code
- Outputs
- Using MPI and OpenMP
- Static Mesh Refinement
- Adaptive Mesh Refinement
- Load Balancing
- Special Relativity
- General Relativity
- Passive Scalars
- Shearing Box
- Diffusion Processes
- General Equation of State
- FFT
- High-Order Methods
- Super-Time-Stepping
- Orbital Advection
- Rotating System
- Reading Data from External Files
Programmer Guide