Julia code for clustering using coarse Ricci curvature
This is some Julia code for performing a Ricci flow clustering algorithm based on the notion of Coarse Ricci curvature: (See the preprint http://arxiv.org/abs/1505.04166 for more discussion of the geometry here.)
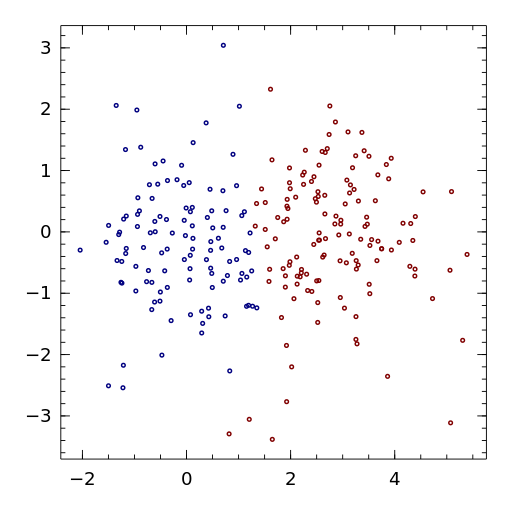
The algorithm seems to work well on clouds of points created from different normal distributions, for example, the picture below is 250 points, half sample from a normal distribution centered at the origin, half sample from a normal distribution centered 3 units to the left.
On other examples involving noisy submanifolds, for example noise_moons or noisy_circles, the Ricci curvature didn't help the algorithm run, in fact, it works better when the Ricci curvature is replaced by distance squared, and then the algorithm becomes essentially a gravitational clustering algorithm
We had another repository in python, this use some of technical algorithms implemented in C and C++ (in particular Floyd-Warscall. After some dependencies got out of whack, I decided to implement this is Julia, where everything can be self-contained and no docker containers are necessary.
To try it, run julia Ricci.jl.
I'm doing a very non-sophisticated thing of created two sets of k points by default, and then if you want to bring in data from a file, you can uncomment some code.
 Contributor micah541 is partially supported by NSF grant DMS-1438359.
Contributor micah541 is partially supported by NSF grant DMS-1438359.