-
Notifications
You must be signed in to change notification settings - Fork 39
Module Trivariate
The module trivariate represents NURBS volumes and contains construction methods and operations related to such volumes.
This module depends on:
- GoTools Core library
- SISL library
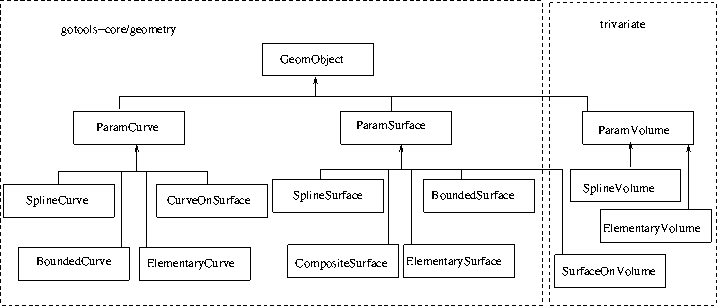
Simplified overview of the geometry class hierarchy
The figure above shows the main geometric classes in GoTools and how they are divided between modules.
A B-spline volume is represented as a SplineVolume in the GoTools module trivariate. The volume is defined by the formula
with control points
The following is a list of the components of the representation:
-
$dim$ : The dimension of the geometry space. -
$n_1$ : The number of control points with respect to the first parameter. -
$n_2$ : The number of control points with respect to the second parameter. -
$n_3$ : The number of control points with respect to the third parameter. -
$k_1$ : The order (polynomial degree + 1) of the B-splines in the first parameter. -
$k_2$ : The order of the B-splines in the second parameter. -
$k_3$ : The order of the B-splines in the third parameter. -
${\bf u}$ : The knot vector of the B-splines with respect to the first parameter,${\bf u} = (u_1,u_2,\ldots,u_{n_1+k_1})$ . -
${\bf v}$ : The knot vector of the B-splines with respect to the second parameter,${\bf v} = (v_1,v_2,\ldots,v_{n_2+k_2})$ . -
${\bf w}$ : The knot vector of the B-splines with respect to the third parameter,${\bf w} = (w_1,w_2,\ldots,w_{n_3+k_3})$ . -
${\bf p}$ : The control points of the B-spline volume,$c_{d,i,j,h}$ ,$d=1,\ldots,dim$ ,$i=1,\ldots,n_1$ ,$j=1,\ldots,n_2$ ,$h=1,\ldots,n_3$ . When$dim = 3$ , we have The volume coefficients are provided in a sequence in the reflected lexicographic order, i.e.,$$(x_{1,1,1}, y_{1,1,1}, z_{1,1,1}), ..., (x_{n_1,1,1}, y_{n_1,1,1}, z_{n_1,1,1}),$$ $$ ...,$$$$(x_{1,n_2,1}, y_{1,n_2,1}, z_{1,n_2,1}), ..., (x_{n_1,n_2,1}, y_{n_1,n_2,1}, z_{n_1,n_2,1}),$$ $$...,...,$$ $$(x_{1,1,n_3}, y_{1,1,n_3}, z_{1,1,n_3}), ..., (x_{n_1,1,n_3}, y_{n_1,1,n_3}, z_{n_1,1,n_3}),$$ $$ ...,$$$$(x_{1,n_2,n_3}, y_{1,n_2,n_3}, z_{1,n_2,n_3}), ..., (x_{n_1,n_2,n_3}, y_{n_1,n_2,n_3}, z_{n_1,n_2,n_3}).$$
The data of the B-spline volume must fulfill the following requirements:
- All knot vectors must be non-decreasing.
- The number of control points must be greater than or equal to the order with respect to all three parameters:
$n_1 \ge k_1$ ,$n_2 \ge k_2$ and$n_3 \ge k_3$ .
The properties of the representation of a B-spline volume are similar to the properties of the representation of a B-spline curve or surface. The control points
A basis function of a B-spline volume, represented by the class BsplineBasis, is the product of three basis functions corresponding to B-spline curves,
$$ B_{i,k_1,{\bf u}}(u) B_{j,k_2,{\bf v}}(v) B_{h,k_3,{\bf w}}(w). $$
Its support is the box
A NURBS (Non-Uniform Rational B-Spline) volume is a generalization of a B-spline volume,
In addition to the data of a B-spline surface, the NURBS volume has weights
The representation of a NURBS volume is the same as for a B-spline volume, except that it also includes a vector
The NURBS volume is represented by SplineVolume. As for the curve and surface cases, the constructor expects the coefficients to be multiplied by the weights.
To a large extent, the functionality of a SplineVolume corresponds to the functionality of a spline surface. Important functionality is:
- A NURBS volume is able to make a copy of itself
- Compute the bounding box of the volume
- Evaluation and grid evaluation
- Grid evaluation of basis functions
- Compute the derivative volume corresponding to a volume
- Closest point computation
- Fetch a sub volume of a given volume
- Fetch information related to the spline spaces
- Swap and reverse parameter directions in a volume
- Fetch the control structure of the volume
- Fetch all weights of a NURBS volume
- Insert knots into the spline spaces of the volume, and adapt the volume description accordingly
- Increase the polynomial degree of the volume in one parameter direction
- Fetch a constant parameter surface from the volume
- Fetch all boundary surfaces surrounding a volume
- Check for periodicity and degeneracy
The following methods exist for construction of a SplineVolume. The corresponding GoTools class method names are given in brackets.
-
SweepVolumeCreator::linearSweptSweep a NURBS surface along a NURBS curve. - Rotational sweep of a NURBS surface
(
SweepVolumeCreator). - Lofting to interpolate a number of NURBS surfaces
(
LoftVolumeCreator). - Interpolate six boundary surface to create a volume using a Coons patch approach
(
CoonsPatchVolumeGen). This functionality applies only to non-rational spline surfaces. - Represent an
ElementaryVolumeas a spline volume. An elementary volume is aParamVolumesimilar toSplineVolume. The elementary volumes are:SphereVolumeCylinderVolumeConeVolumeParallelepipedTorusVolume
A spline volume may have a well-behaved outer boundary, but a bad distribution of coefficients in the interior. This is in particular the case if the volume is constructed by a Coons patch approach. The positioning of the internal coefficients may be improved by smoothing. The coefficients at the boundaries are kept fixed and the coefficients in the interior are redistributed by solving a minimization problem. The smoothing is performed in the class SmoothVolume.
The module trivariate provides a SurfaceOnVolume class, which extends the class of parametric surfaces defined in gotools-core/geometry submodule. This surface inherits most of the functionality defined for parametric surfaces and takes the same role as CurveOnSurface for parametric curves. The surface possesses information about
- The associated volume
- The geometric description of this surface and/or
- The description of this surface in the parameter domain of the given volume
- Constant parameter and volume boundary information. If this surface for instance happens to be a constant parameter surface in the given volume, it knows the parameter direction and the associated constant parameter value.
Two evaluator based curves can be used together with HermiteAppC in the gotools-core/creators submodule exist, namely VolumeParameterCurve and VolumeSpaceCurve.
Getting started
Miscellaneous
Functionality
- Modules
- gotools-core
- compositemodel
- implicitization
- igeslib
- intersections
- isogeometric_model
- lrsplines2D
- parametrization
- qualitymodule
- topology
- trivariate
- trivariatemodel
- viewlib
Dependencies