-
Notifications
You must be signed in to change notification settings - Fork 248
[KratosStructuralMechanicsAPI] Constitutive laws in Structural Mechanics Application
The objective of this text is to describe qualitatively the general framework developed in the Structural Mechanics Application related to the "Constitutive Law" problem in engineering. The main point of focus is the description of various constitutive models based on phenomenological hyperelasticity, elastoplasticity, damage, viscoelasticity and elasto-viscoplasticity.
Since this is a work-in-progress, we are going to describe the present state of the Application but some other constitutive models will be added in the future. This is why we encourage you to propose new methodologies to be implemented. We are always willing to develop some useful tools for other engineers and professionals.
At this point, there are some Constitutive Laws (CL from now on) that are available and ready to use:
- Isotropic Elasticity (2D, 3D, Axisymmetric, truss, beam)
- HyperElasticity (2D, 3D)
- Isotropic Plasticity (3D)
- Small Strain Isotropic Damage
- Small Strain d+d- Damage
- ViscoElasticity
- ViscoPlasticity
- Parallel Rule of Mixtures
- Serial Parallel Rule of Mixtures
- Adding an initial state: initial strain/stress/F
- High Cycle Fatigue
- Appendix
- References
A description of the previous models will be done in the following paragraphs.
This is the most simple CL but also one of the most used. Isotropic materials require two material parameters only, the Young modulus E and the Poisson's ratio v. The constitutive matrix for isotropic materials can be directly written in global cartesian axes. If initial strains and stresses are taken into account we can write:
σ=D : ε
being ε the strain tensor assuming small strains and D the Elastic Isotropic Constitutive Matrix expressed as:
The procedure is analogous with the 2D and axisymmetric case.
It can be shown that the stored strain energy (potential) for a hyperelastic material which is isotropic with respect to the initial, unstressed configuration can be written as a function of the principal invariants (I1, I2, I3) of the right Cauchy–Green deformation tensor. The principal invariants of a second-order tensor and their derivatives figure prominently in elastic and elastic–plastic constitutive relations. [5]
Many engineering applications involve small strains and large rotations. In these problems the effects of large deformation are primarily due to rotations (such as in the bending of a marineriser or a fishing rod). The response of the material may then be modeled by a simple extension of the linear elastic laws by replacing the stress by the PK2 stress and the linear strain by the Green strain. This is called a Saint Venant–Kirchhoff material, or a Kirchhoff material for brevity. The most general Kirchhoff model is:
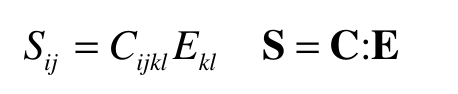
The definition of the of the constitutive tensor for the Kirchoff model is:
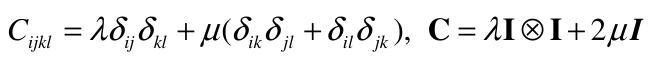
The two independent material constants l and m are called the Lamé constants. The stress–strain relation for an isotropic Kirchhoff material may therefore be written as:
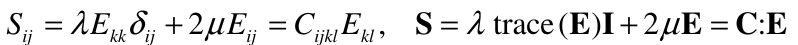
The Lamé constants can be expressed in terms of other constants which are more closely related to physical measurements, the bulk modulus K, Young’s modulus E and Poisson’s ratio v, by:
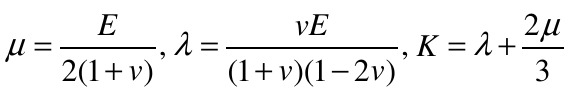
The Neo-Hookean material model is an extension of the isotropic linear law (Hooke’s law) to large deformations. The stored energy function for a compressible Neo-Hookean material (isotropic with respect to the initial, unstressed configuration) is:
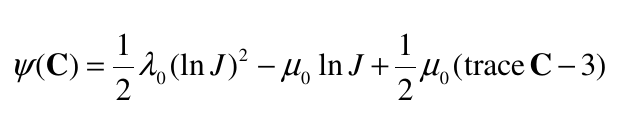
The stresses are given by:
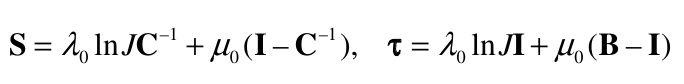
The elasticity tensors:
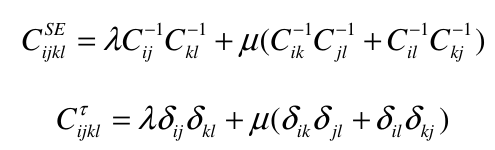
In order to understand the structure of the plasticity CL one can see the methodology as a set of Matryoshka dolls as shown in the following picture:

In which each object is "templated" inside the bigger one. In this sense the registration of the Plasticity Laws follows the same idea:
GenericSmallStrainIsotropicPlasticity<GenericConstitutiveLawIntegratorPlasticity<VonMisesYieldSurface<ModifiedMohrCoulombPlasticPotential<6>>>>
In this case we have registered a Plasticity CL using the Von Mises YS and a Modified Mohr Coulomb PP.
This object is used to determine whether the strain/stress tensor is in elastic or plastice regime. There are several classical yield surfaces available right now:
- Rankine
- Tresca
- Von Mises (J2)
- Modified Mohr Coulomb (see appendix)
- Drucker-Prager
- Simo-Ju
- Classical Mohr-Coulomb
The general definition of the yield surface class is as follows:
template<class TPlasticPotentialType>
class KRATOS_API(STRUCTURAL_MECHANICS_APPLICATION) DruckerPragerYieldSurfaceAs explained before, the Plasticity constitutive Law could use one yield surface and a different plastic potential surface (so-called non-associative plasticity) so we had to develop a strategy to allow different YS-PP combinations without repeating code. This was done again, by including the PP as a template for the Yield Surface.
This object is used to compute the derivatives of the Plastic potential surfaces in order to calculate the direction of the plastic strain. The general definition of the PP is:
template <SizeType TVoigtSize = 6>
class KRATOS_API(STRUCTURAL_MECHANICS_APPLICATION) DruckerPragerPlasticPotentialThere are several classical plastic potential surfaces available:
- Tresca
- Von Mises (J2)
- Modified Mohr-Coulomb (see appendix)
- Drucker-Prager
- Classical Mohr-Coulomb
It is important to mention that the Tresca, Modified Mohr-Coulomb and the classical Mohr-Coulomb have been smoothed when the stress state is close to the edges of the yield surface. In the case of Tresca the surface is smoothed with Von-Mises whereas in the case of Mohr-Coulomb is smoothed with Drucker-Prager.
We have implemented a plasticity algorithm that allows the following evolution laws of the yield surface: linear hardening (0), exponential hardening (1), initial hardening exponential softening (2), perfect plasticity (3), fitting hardening (4) and linear exponential softening (5).
- Linear Softening (0)
- Exponential Hardening (1)
- Initial Hardening Exponential Softening (2)
- Perfect Plasticity (3)
- Curve Fitting Hardening (4)
- Linear Exponential Softening (5)
The previous curves can be seen in the following graph:

The Initial Hardening Exponential Softening is a parabolic hardening. To use it, it is necessary to include the following variables:
MAXIMUM_STRESS-
MAXIMUM_STRESS_POSITION: Value between 0 and 1. Recommended values are between 0.2-0.6. Defines the fit to the fracture energy The fitting hardening describes the stress-strain curve by diving and defining it in three regions as shown in the previous figure. It has only been developed for Von Mises.
Region 1
To define the first region, it is necessary to add the following parameter:
-
CURVE_FITTING_PARAMETERS: It is a vector that must be noted [ a0,a1,…,an] where n is the polynomial degree that tries to describe the 1st region of the stress-strain curve.
It is not recommendable to use high degrees’ polynomials.
Region 2
The second section is linear and to define it, the following parameters must be included:
-
TANGENCY_REGION2: It defines the step from region 1 to 2 and can be horizontal (0) or sloping (1). -
PLASTIC_STRAIN_INDICATOR: The vector [Ep1, Ep2] defines the beginning (Ep1) and end (Ep2) points of the second region.
Region 3
Final section of the curve with exponential softening.
The linear exponential softening combines both behaviours. To use it, the following parameter must be added:
-
PLASTIC_DISSIPATION_LIMIT_LINEAR_SOFTENING: It can take values from 0 to 1. The closer to 0 the softening will have a more exponential behaviour and the closer to 1 it will be more linear.
The theory of plasticity is concerned with solids that, after being subjected to a loading programme, may sustain permanent (or plastic) deformations when completely unloaded. In particular, this theory is restricted to the description of materials (and conditions) for which the permanent deformations do not depend on the rate of application of loads and is often referred to as rate-independent plasticity.
It is important to remark that the model presented here is restricted to infinitesimal deformations but some large strain models are going to be implemented in the future. As usual, this constitutive law requires a Yield Surface (YS) in order to detect de non-linear behaviour and a Plastic Potential (PP) to describe the direction of the plastic strain.
Since there are several options to be used for YS and PP and taking into account that they can be combined in any way, we have developed a method of assembling them as required, automatically, by using a factory procedure.
The more general file is called generic_small_strain_isotropic_plasticity.cpp and the main method is CalculateMaterialResponseCauchy as follows:
template <class TConstLawIntegratorType>
void GenericSmallStrainIsotropicPlasticity<TConstLawIntegratorType>::CalculateMaterialResponseCauchy(ConstitutiveLaw::Parameters& rValues)As can be seen in the previous figure, the Constitutive Law has a template named "TConstLawIntegratorType" which is the object that integrates the stress in order to return to the admissible stress level according to a certain yield stress.
Inside this Integrator the return mapping loop is performed. Since there are several procedures to do that, it was necessary to include the Integrator as a template. Currently we have implemented the so called Backward Euler Return Mapping.
template<class TYieldSurfaceType>
class KRATOS_API(STRUCTURAL_MECHANICS_APPLICATION) GenericConstitutiveLawIntegratorPlasticityAs can be seen in the previous figure, the ConstitutiveLawIntegratorPlasticity has a template regarding the Yield Surface object. This was done in order to allow to use any kind of yield surface according to the preferences of the users.
The main hypothesis underlying the finite strain elastoplasticity constitutive framework described here is the multiplicative decomposition of the deformation gradient, F , into elastic and plastic contributions; that is, it is assumed that the deformation gradient can be decomposed as the product F = Fe x Fp, where F and F are named, respectively, the elastic and plastic deformation gradients.
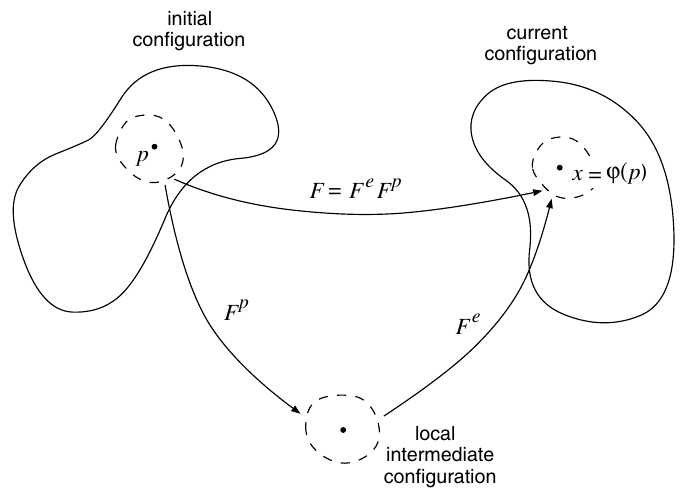
The crucial difference between the discretisation of the large strain problem and the infinitesimal one lies in the numerical approximation of the plastic flow equation. The structure of the plastic flow equation makes algorithms based on exponential map integrators.
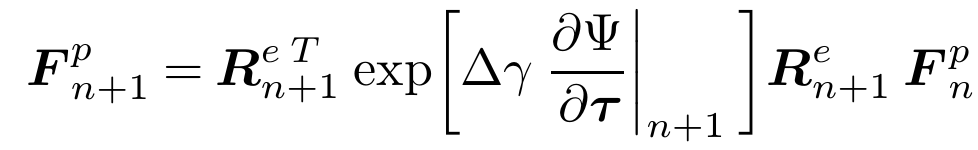
This Constitutive law has some checks in order to verify that all the parameters are provided but, very briefly, we are going to describe those parameters in order to perform a calculation. The generic StructuralMaterials.json has the following structure:
{
"model_part_name" : "Parts_Shell",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicPlasticityFactory3D",
"yield_surface" : "VonMises",
"plastic_potential" : "VonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"YIELD_STRESS_TENSION" : 275.0e6,
"YIELD_STRESS_COMPRESSION" : 275.0e6,
"FRACTURE_ENERGY" : 1.0e5,
"HARDENING_CURVE" : 1,
"MAXIMUM_STRESS" : 300.0e6,
"MAXIMUM_STRESS_POSITION" : 0.3
},
"Tables" : {}
}
}The parameters needed for the plasticity (neglecting the young modulus and poisson ratio) are (use International System):
- yield_surface : Defines the yield surface to use
- plastic_potential : Defines the plastic potential to use
-
FRACTURE_ENERGY: Defines the maximum energy that the system can dissipate at each integration point -
YIELD_STRESS_COMPRESSION: Maximum yield strength in compression -
YIELD_STRESS_TENSION: Maximum yield strength in tension -
HARDENING_CURVE: Defines the flow rule to use (LinearSoft=0, ExpSoft=1, Hardening=2, PerfPlast=3) -
MAXIMUM_STRESS_POSITION: ONLY FOR CURVE 2, Defines the position of the peak strength (value ranging 0-1) -
MAXIMUM_STRESS: ONLY FOR CURVE 2, Defines the peak strength value -
FRICTION_ANGLE: Defines the friction angle value in degrees -
DILATANCY_ANGLE: Defines the dilatancy angle value in degrees (usually 0.5*friction_angle)
Continuum damage mechanics is a branch of continuum mechanics that describes the progressive loss of material integrity due to the propagation and coalescence of micro-cracks, micro-voids, and similar defects. These changes in the microstructure lead to an irreversible material degradation, characterized by a loss of stiffness that can be observed on the macro-scale.
The structure of the damage constitutive law is analogous to the plasticity case. Indeed, the damage constitutive law (generic_small_strain_isotropic_plasticity.cpp) has a template of an integrator that calculates the damage internal variable and computes the integrated or real stress according to the degradation of the material. This damage CL uses the Yield Surfaces previously described in an identical way as the plasticity. If you want more information about the template structure I recommend you to see the plasticity chapter where it is detailed.
The general StructuralMaterials.json have the following structure:
{
"model_part_name" : "Parts_Shell",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicDamageFactory3D",
"yield_surface" : "VonMises"
"plastic_potential" : "VonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"YIELD_STRESS_TENSION" : 275.0e6,
"YIELD_STRESS_COMPRESSION" : 275.0e6,
"FRICTION_ANGLE" : 32.0,
"SOFTENING_TYPE" : 1
},
"Tables" : {}
}
}The parameters are the following (use International System):
- yield_surface : Defines the yield surface to use
- plastic_potential : Defines the plastic potential to use (not used in damage)
-
FRACTURE_ENERGY: Defines the maximum energy that the system can dissipate at each integration point -
YIELD_STRESS_COMPRESSION: Maximum yield strength in compression -
YIELD_STRESS_TENSION: Maximum yield strength in tension -
FRICTION_ANGLE: Defines the friction angle value in degrees -
SOFTENING_TYPE: Defines the softening type (linear softening=0, exponential softening=1)
Another example of the file is shown below.
{
"properties" : [{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto1",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicDamage3DVonMisesVonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"YIELD_STRESS" : 3E6,
"FRACTURE_ENERGY" : 40,
"SOFTENING_TYPE" : 1,
"TANGENT_OPERATOR_ESTIMATION" : 2
},
"Tables" : {}
}
}]
}The names of the constitutive laws are described in the correspondent section and all the names can be found in the following file:
D:\Kratos\applications\ConstitutiveLawsApplication\constitutive_laws_application.cpp
The basic variables that the StructuralMaterials.json file must contain are listed and described below.
-
DENSITY: -
YOUNG_MODULUS: -
POISSON_RATIO: -
YIELD_STRESS: -
FRACTURE_ENERGY: -
SOFTENING_TYPE: -
TANGENT_OPERATOR_ESTIMATION: (not mandatory to run the case. View section Non-Linear Simulations tips)
Fracture energy
View (Part Non-Linear Simulations tips) to choose the most suitable value.
Softening type
Three different softenings have been implemented: linear hardening (0), exponential hardening (1) and hardening damage (2).

The hardening damage simulates a parabolic hardening. To use it, it is necessary to include the following variables in the file:
* MAXIMUM_STRESS
In this case, we have implemented a more sophisticated damage model that differentiates the behaviour of the material depending on the sign of the stresses. In other words, the damage behaviour is different in compression and tension. This is done by performing an Spectral Decomposition of the Stress Tensor (see constitutive_law_utilities.cpp) in which we separate the tension/compression states [2,3].
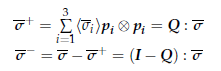
Once we have Decomposed the stress tensor we proceed to the calculation of the damage variables (now d+ and d- corresponding to the tension/compression damage) and compute the integrated stress tensor as:
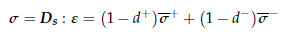
In order to guarantee flexibility, we have designed an structure capable of combining different yield surfaces in tension and in compression. This has been achieved by templating two integrators named TConstLawIntegratorTensionType and TConstLawIntegratorCompressionType which define the tension/compression yield surfaces and flow rules.
The implementation is described below (generic_small_strain_d_plus_d_minus_damage.cpp):
template <class TConstLawIntegratorTensionType, class TConstLawIntegratorCompressionType>
class KRATOS_API(STRUCTURAL_MECHANICS_APPLICATION) GenericSmallStrainDplusDminusDamageThe general StructuralMaterials.json has the following form:
{
"model_part_name" : "Parts_Shell",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainDplusDminusDamageModifiedMohrCoulombVonMises3D"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"FRACTURE_ENERGY" : 1.5e2,
"FRACTURE_ENERGY_COMPRESSION" : 1.0e2,
"YIELD_STRESS_TENSION" : 3.0e6,
"YIELD_STRESS_COMPRESSION" : 1.0e6,
"FRICTION_ANGLE" : 32.0,
"DILATANCY_ANGLE" : 16.0,
"SOFTENING_TYPE" : 1
},
"Tables" : {}
}
}The parameters required for this model have been explained previously and the way of combining yield surfaces is by calling the already registered combinations of them. For instance, in this example the name of the law is SmallStrainDplusDminusDamageModifiedMohrCoulombVonMises3D so it means that we are using a d+d- damage model using a Modified Mohr Coulomb yield surface for tension and Von Mises for compression. In this way we define the combinations by typing as "name":
SmallStrainDplusDminusDamage<TensionYieldSurface,CompressionYieldSurface>3D and the yield surfaces (keywords) available are, as explained before:
- Rankine
- Tresca
- VonMises
- ModifiedMohrCoulomb
- DruckerPrager
- SimoJu
- Classical Mohr-Coulomb
One of the behaviors responsible for the nonlinearity in the materials’ response over the time field is due to viscoelasticity. Viscoelasticity studies the rheological behavior of materials, in other words, behaviors affected by the course of time.
Up to now, we have developed two viscous models: the Generalized Maxwell model (used to simulate the stress relaxation of materials) and the Generalized Kelvin model (used to simulate creep and delayed strains).
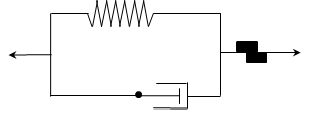
This viscoelastic model has been widely used when simulating the stress relaxation of materials subjected to a constant strain rate (like in pre-stressing tendons used in civil engineering). The spring-damper diagram is (see [1] for more information) as follows:
And the general behaviour of the model can be seen in the picture below [1]:
The general StructuralMaterials.json have the following structure:
{
"model_part_name" : "Parts_Shell",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "ViscousGeneralizedMaxwell3D"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"VISCOUS_PARAMETER" : 0.15,
"DELAY_TIME" : 1.0
},
"Tables" : {}
}
}The parameters are the following:
-
DELAY_TIME: Defines the initial slope of the curve (see previous figure) -
VISCOUS_PARAMETER: Is the ratio between the stiffnesses C1/Cinf
This viscous model has been used in general to simulate delayed strains in materials such as the creep in concrete and soils. The spring-damper diagram is (see [1] for more information) as follows:
And the general behaviour of the model can be seen in the picture below [1]:
The general StructuralMaterials.json have the following structure:
{
"model_part_name" : "Parts_Shell",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "ViscousGeneralizedKelvin3D"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 206900000000.0,
"POISSON_RATIO" : 0.29,
"DELAY_TIME" : 150.0
},
"Tables" : {}
}
}The parameters are the following:
-
DELAY_TIME: Defines the initial slope of the curve (see previous figure)
In this case we were seeking a constitutive law that allows the material to develop plastic strains as well as a certain stress relaxation along time. This can be achieved with the formulation proposed but some other procedures will be implemented to increase the variety and polivalence of the Structural Mechanics Application.
The spring damper scheme for this methodology is shown below and allows the material to plastify and, in a viscous way, relax the stress along time.
The case is composed by the following files:
- ProjectParameters.json
- MainKratos.py
- Example.mdpa
- StructuralMaterials.json
The generic StructuralMaterials.json has the following structure:
{
"properties" : [{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto1",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "ParallelRuleOfMixturesLaw3D",
"combination_factors" : [0.5, 0.5]
},
"Variables" : {
"DENSITY" : 7850.0,
"LAYER_EULER_ANGLES": [0,0,0,0,0,0]
},
"Tables" : {}
},
"sub_properties" : [{
"properties_id" : 11,
"Material" : {
"constitutive_law" : {
"name" : "LinearElastic3DLaw"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 31E9,
"POISSON_RATIO" : 0.35
},
"Tables" : {}
}
},{
"properties_id" : 12,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicDamage3DVonMisesVonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 35E9,
"POISSON_RATIO" : 0.2,
"YIELD_STRESS" : 1.5E6,
"FRACTURE_ENERGY" : 70,
"SOFTENING_TYPE" : 1,
"TANGENT_OPERATOR_ESTIMATION" : 2
},
"Tables" : {}
}
}]
}]
}Notice that the file is divided into the general properties of the solid and the sub_properties of the components. Then, there will be a constitutive law applied to the solid (in this case is ParallelRuleOfMixturesLaw3D) and different constitutive laws applied to the "sub_properties". The combination_factors variable is a vector composed by the volumetric participations of fibre and matrix. As known, the total of the volumetric participations must be 1.
The orientation of the fibres is defined as a vector in the parameter LAYER_EULER_ANGLES and must be expressed in degrees.
The variables that the sub_properties contain depend on the constitutive law. Following this division of the file into solid and components, the properties_id is a reference order to the object that is going to be described. It is recommendable to use one single number to describe the solid (1, 2, 3, …, etc.) and combinations to describe the components (11, 12, 1,3, …, 21, 22, 23, …, etc.).
The simulation of a composite can be carried out in two ways depending on whether the model is understood as a whole solid (SerialParallel) or as each of its components separately (Micromodel).
In order to describe both procedures, an example of a block of composite material formed by a single layer with the fibres oriented at 900 will be followed.
Micromodel
As shown in the figure the micro-model geometry of the composite has been generated considering the fibre and matrix separately.
The case is composed by the following files:
- ProjectParameters.json
- MainKratos.py
- Example.mdpa
- StructuralMaterials.json
The generic StructuralMaterials.json has the following structure:
{
"properties" : [{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto1",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicDamage3DVonMisesVonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 1.3E7,
"POISSON_RATIO" : 0.325,
"YIELD_STRESS" : 4.3323E7,
"FRACTURE_ENERGY" : 1000E5,
"SOFTENING_TYPE" : 1,
"TANGENT_OPERATOR_ESTIMATION" : 2
},
"Tables" : {}
}
},{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto2",
"properties_id" : 2,
"Material" : {
"constitutive_law" : {
"name" : "LinearElastic3DLaw"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 23.9551E7,
"POISSON_RATIO" : 0.0
},
"Tables" : {}
}
}]
}As it can be noticed, the properties of each solid are described separately as a regular case.
Serial Parallel model
As shown in the figure, the Parallel Series model geometry that has been generated is a single block.
The case is composed by the following files:
- ProjectParameters.json
- MainKratos.py
- Example.mdpa
- StructuralMaterials.json
The generic StructuralMaterials.json has the following structure:
{
"properties" : [{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto1",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SerialParallelRuleOfMixturesLaw",
"combination_factors" : [0.88, 0.12],
"parallel_behaviour_directions" : [0,1,0,0,0,0]
},
"Variables" : {
},
"Tables" : {}
},
"sub_properties" : [{
"properties_id" : 11,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainIsotropicDamage3DVonMisesVonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 1.3E7,
"POISSON_RATIO" : 0.325,
"YIELD_STRESS" : 4.3323E7,
"FRACTURE_ENERGY" : 1000E5,
"SOFTENING_TYPE" : 1,
"TANGENT_OPERATOR_ESTIMATION" : 2
},
"Tables" : {}
}
},{
"properties_id" : 12,
"Material" : {
"constitutive_law" : {
"name" : "LinearElastic3DLaw"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 23.9551E7,
"POISSON_RATIO" : 0.0
},
"Tables" : {}
}
}]
}]
}For this procedure it is necessary to use the constitutive law SerialParallelRuleOfMixturesLaw indicating in the parameter combination_factors the volumetric participations of the fiber and the matrix. The total must be 1.
The parameter "parallel_behavior_directions" is a six component vector that indicates the direction in which the fibers of the composite are oriented, assigning the value 1 to the direction.
The parameters necessary to describe the properties of the fibre and the matrix will be those required by the constitutive law used.
In the case of having different layers, it is necessary to add the following parameters:
-
"combination_factors": vector of two components that indicates the volumetric participation of each layer of composite. The total be 1.
-
"LAYER_EULER_ANGLES": vector of six components that indicates the orientation of the layer.
In the case of having fibres with orientations other than 0 and 90, the fibres oriented at 00 should be considered and rotate the entire layer adding the necessary parameters for more than one layer.
Currently, there is the option to add an initial state at each integration point of the model. This can be done in several ways depending of your needs. If the constitutive law used has this capability (some of them have it currently, see this CL as an example) the only thing that has to be done is:
- Option one: use the .mdpa
In order to apply this initial strain/stress we have used the mdpa feature of
Begin ElementalData INITIAL_STRESS_VECTOR
1 [6] (0,0,1e6,0,0,0)
2 [6] (0,0,1e6,0,0,0)
3 [6] (0,0,1e6,0,0,0)
4 [6] (0,0,1e6,0,0,0)
End ElementalData
Begin ElementalData INITIAL_STRAIN_VECTOR
1 [6] (0.01,0.01,0.01,0,0,0)
2 [6] (0.01,0.01,0.01,0,0,0)
3 [6] (0.01,0.01,0.01,0,0,0)
4 [6] (0.01,0.01,0.01,0,0,0)
End ElementalData
And in this way the element geometry (and each constitutive law) will have access and the possibility to apply it.
- Option two: use the python process
set_initial_state_process.py
In this approach you only have to add in your ProjectParameters.json the following block in processes:
{
{
"python_module" : "set_initial_state_process",
"kratos_module" : "KratosMultiphysics",
"process_name" : "set_initial_state_process",
"Parameters" : {
"mesh_id" : 0,
"model_part_name" : "Structure",
"dimension" : 2,
"imposed_strain" : [0.0,0.00,0],
"imposed_stress" : [1000000,0,0],
"imposed_deformation_gradient" : [[1,0],[0,1]],
"interval" : [0.0, 1e30]
}
}And the constitutive law will do the rest :).
The implementation of the constitutive la can be found in:
generic_small_strain_high_cycle_fatigue_law.hgeneric_small_strain_high_cycle_fatigue_law.cpphigh_cycle_fatigue_law_integrator.h
Four files are needed to run a HCF case with Kratos:
-
.mdpa- contains the geometrical information of the finite element mesh used and the groups created to be assign for BC / imp disp / imp loads -
material.json- contains the material(s) properties. -
parameters.json- contains the information of the case to be run (BC, imp. disp, imp. loads, advance in time strategy, output variables, etc.) -
MainKratos.py- executable file; here the analysis_stage that is runned is selected.
Examples for all of them (except for .mdpa which does not change from other cases) are shown.
The generic StructuralMaterials.json has the following structure:
{
"properties" : [{
"model_part_name" : "Structure.Parts_Solid_Solid_Auto1",
"properties_id" : 1,
"Material" : {
"constitutive_law" : {
"name" : "SmallStrainHighCycleFatigue3DLawVonMisesVonMises"
},
"Variables" : {
"DENSITY" : 7850.0,
"YOUNG_MODULUS" : 2.1E11,
"POISSON_RATIO" : 0.29,
"YIELD_STRESS" : 200E6,
"FRACTURE_ENERGY" : 10E5,
"SOFTENING_TYPE" : 1,
"HIGH_CYCLE_FATIGUE_COEFFICIENTS": [0.41807, 1.575, 0.6, 0.00226, 5.58, 0.0003, 0.002]
},
"Tables" : {}
}
}]
}The name of the constitutive law follows the structure:
“SmallStrainHighCycleFatigue3DLawYieldSurfaceName”
As shown in the previous example, the variable “HIGH_CYCLE_FATIGUE_COEFFICIENTS” must be added. This variable is an array of seven components [Su, STHR1, STHR2, ALFAF, BETAF, AUXR1, AUXR2].
The following block must be added to the ProjectParameters.json script.
"fatigue": {
"advancing_strategy" : true,
"advancing_strategy_cycles" : 1.0e12,
"advancing_strategy_time" : 1.0e12,
"constraints_process_list" : ["Structure.DISPLACEMENT_Displacement_Auto1", "Structure. DISPLACEMENT_Displacement_Auto2"],
"loads_process_list" : [],
"advancing_strategy_damage" : 600.0,
"element_gausspoint_print" : [1, 0],
"node_print" : 1
}The MainKratos.py must be modified following:
from __future__ import print_function, absolute_import, division
import KratosMultiphysics
from KratosMultiphysics.ConstitutiveLawsApplication.high_cycle_fatigue_analysis import HighCycleFatigueAnalysis
"""
For user-scripting it is intended that a new class is derived
from StructuralMechanicsAnalysis to do modifications
"""
if __name__ == "__main__":
with open("ProjectParameters.json", 'r') as parameter_file:
parameters = KratosMultiphysics.Parameters(parameter_file.read())
model = KratosMultiphysics.Model()
simulation = HighCycleFatigueAnalysis(model,parameters)
simulation.Run()Post files
In addition to the “.gid/.vtk” output obtained from the calculation, from the HCF calculation two extra files are obtained.
-
PlotNode.txt- Info: Time vs Displacement at a node of the FE mesh. -
PlotElement.txt- Info: main variables of the problem for a GP of the FE mesh.
The Mohr-Coulomb function cannot be used directly in frictional cohesive materials such as concrete, which has an internal friction angle of φ≅32 According to the Mohr- Coulomb classic formulation, a limit strength relation is obtained for this angle between a traction behavior and a uniaxial compression behavior of tan[(π / 4) + (φ / 2)]= 3,25. This magnitude is very different from the concrete magnitude, which should be around 10. To solve this problem, either the friction angle can be increased causing a dilatancy excess or the original criterion can be modified. By this last option, the following expression is obtained,
F(σ) = f(σ) - c
where the stress function "f" is expressed as[1] (being θ the Lode's angle, I1, J2 the classical stress invariants and φ the friction angle):
Through this new Mohr-Coulomb modified function any strength relation required by the different materials can be established by only modifying Ki , without increasing dilatancy.
The values of the Ki and the parameters required can be seen in the figures below[1].
- Fracture energy
Elegir la energía de fractura más adecuada es importante para asegurar una buena convergencia de la simulación.
Knowing that the energy fracture (gf) is the area under the stress-strain curve in damage or plasticity and that the fracture energy (Gf) of the material is:
The minimum fracture energy can be obtained as:


Tangent operator estimation
The following numerical techniques have been developed to obtain the tangent constitutive matrix.
- Analytic (0)
- FirstOrderPerturbation (1)
- SecondOrderPerturbation (2)
- Secant (3):
- SecondOrderPerturbationV2 (4)
The secant type is the most robust but slower option.
Other alternative options (1,2,4) are based on the derivatives approximation via finite differences. An approximation of the tangent constitutive tensor can be obtained by defining small perturbations of the strain tensor to obtain stress tensor increments. Type 1 operates forward whereas 2 operates with central differences.
Second order perturbation is set by default.
The tangent tensor obtained via perturbation method achieves an average slope close to the expected quadratic behaviour whereas the classical secant tensor reduces linearly with the number of iterations performed.
The implementation can be found in: tangent_operator_calculator_utility.h
This procedure is only called in loading conditions. Otherwise, secant type(damage) or analytic(plasticity) constitutive tensor must be used.
The description of the numerical techniques can be found in A.Cornejo. A fully Langrangian formulation for fluid-structure interaction between free-surface flows and multi-fracturing solids and structures.
[1] "Dinámica no lineal" by S. Oller.
[2] "An Energy-Equivalent d+/d- Damage Model with Enhanced Microcrack Closure-Reopening Capabilities for Cohesive-Frictional Materials" by M. Cervera and C.Tesei.
[3] "A Strain-Based Plastic Viscous-Damage Model for Massive Concrete Structures" by R. Faria, J. Oliver and M. Cervera.
[4] "Computational methods for plasticity. Theory and applications" by EA de Souza Neto, D Perić and DRJ Owen
[5] "Non-linear Finite Elements for continua and structures" by Ted Belytschko, Wing Kam Liu, Brian Moran and Khalil I. Elkhodary
[6]"A fully Lagrangian formulation for fluid-structure interaction problems with free-surface flows and fracturing solids" by Alejandro Cornejo, Alessandro Franci, Francisco Zárate and Eugenio Oñate.
If you have any doubts about the Constitutive Laws in the Structural Mechanics Application do not hesitate to contact us at [email protected], [email protected] and [email protected].
- Getting Kratos (Last compiled Release)
- Compiling Kratos
- Running an example from GiD
- Kratos input files and I/O
- Data management
- Solving strategies
- Manipulating solution values
- Multiphysics
- Video tutorials
- Style Guide
- Authorship of Kratos files
- Configure .gitignore
- How to configure clang-format
- How to use smart pointer in Kratos
- How to define adjoint elements and response functions
- Visibility and Exposure
- Namespaces and Static Classes
Kratos structure
Conventions
Solvers
Debugging, profiling and testing
- Compiling Kratos in debug mode
- Debugging Kratos using GDB
- Cross-debugging Kratos under Windows
- Debugging Kratos C++ under Windows
- Checking memory usage with Valgind
- Profiling Kratos with MAQAO
- Creating unitary tests
- Using ThreadSanitizer to detect OMP data race bugs
- Debugging Memory with ASAN
HOW TOs
- How to create applications
- Python Tutorials
- Kratos For Dummies (I)
- List of classes and variables accessible via python
- How to use Logger
- How to Create a New Application using cmake
- How to write a JSON configuration file
- How to Access DataBase
- How to use quaternions in Kratos
- How to do Mapping between nonmatching meshes
- How to use Clang-Tidy to automatically correct code
- How to use the Constitutive Law class
- How to use Serialization
- How to use GlobalPointerCommunicator
- How to use PointerMapCommunicator
- How to use the Geometry
- How to use processes for BCs
- How to use Parallel Utilities in futureproofing the code
- Porting to Pybind11 (LEGACY CODE)
- Porting to AMatrix
- How to use Cotire
- Applications: Python-modules
- How to run multiple cases using PyCOMPSs
- How to apply a function to a list of variables
- How to use Kratos Native sparse linear algebra
Utilities
Kratos API
Kratos Structural Mechanics API