-
Notifications
You must be signed in to change notification settings - Fork 0
Quantum Computation and Quantum Information
本页为Quantum Computation and Quantum Information读书笔记
本书结构如下
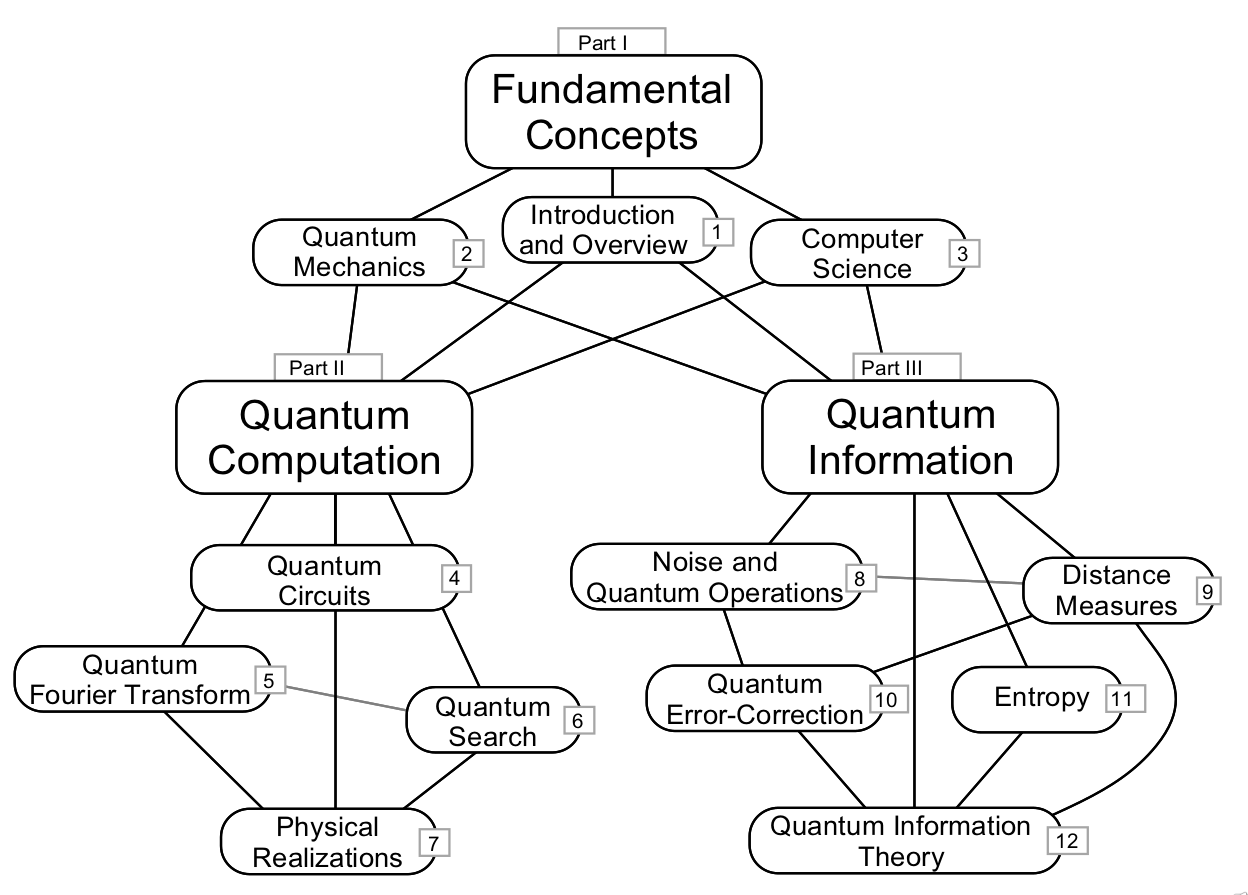
单量子比特可以使用Bloch球表示
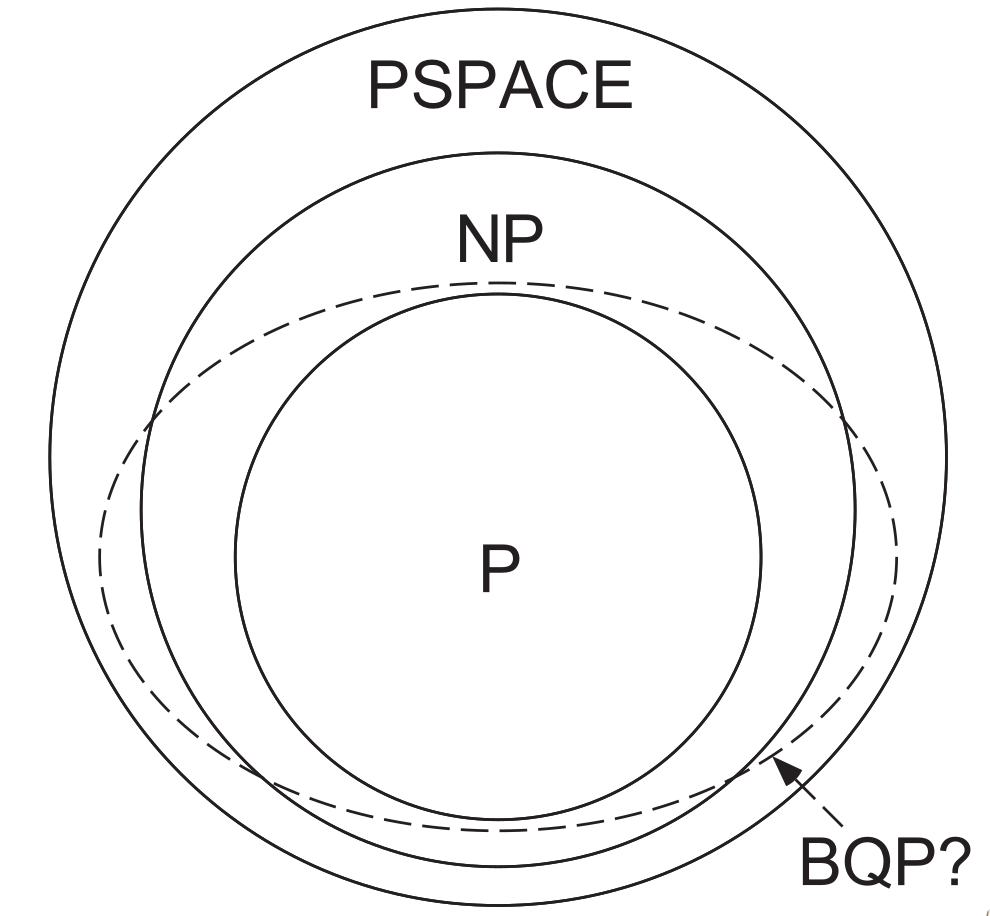
P:可以用经典计算机快速解决的问题
NP:可以用经典计算机快速验证的问题
BPP:可以利用随机算法在一定误差概率限制下快速解决的问题
BQP:可以利用量子计算机在一定误差概率限制下快速解决的问题
PSPACE:可以利用较少的空间资源解决的问题,对时间资源不做要求
(快速指可以在多项式时间内解决)
- 辨别量子力学中静态资源的基本类别
- 辨别量子力学中动态过程的基本类别
- 量化进行动态处理引起的资源交换
-
对于任意一个孤立的物理体系而言,都有一个与之对应,可以定义内积的矢量空间,即Hilbert空间。该空间被称为这个系统的态空间。这个体系可以被态空间中的单位矢量,态矢量完全描述。
-
封闭量子体系的演化用酉变换描述。也就是说,$t_1$时刻系统的$|\psi\rangle$态与$t_2$时刻系统的$|\psi'\rangle$态通过一个仅依赖于时间$t_1$,$t_2$的酉算符进行关联 $$ |\psi'\rangle=U|\psi\rangle $$
量子力学体系随时间的演化通过薛定谔方程描述
$$ i\hbar\frac{d|\psi\rangle}{dt}=\hat{H}|\psi\rangle $$
-
量子测量通过测量算符集$\left\lbrace M_{m}\right\rbrace$描述。它们是作用在正在被测量的态空间上的算符。下标$m$代表实验中可能出现的测量结果。如果在测量前一个时刻量子体系的状态为$|\psi\rangle$,那么测量结果$m$的出现概率为 $$ p(m)=\langle\psi|M_m^\dagger M_m|\psi\rangle $$ 测量之后的量子态为 $$ \frac{M_m|\psi\rangle}{\sqrt{\langle\psi|M_m^\dagger M_m|\psi\rangle}} $$ 测量算符满足完备性条件 $$ \sum_{m} M_{m}^{\dagger} M_{m}=I $$
完备性方程展示了概率和为一的事实 $$ 1=\sum_{m} p(m)=\sum_{m}\left\langle\psi\left|M_{m}^{\dagger} M_{m}\right| \psi\right\rangle $$
-
复合物理体系的态空间是子系统态空间的张量积
投影测量通过一个可观测量$M$描述。它是被观测系统态空间中的厄米算符。这个可观测量具有谱分解 $$ M=\sum_{m} m P_{m} $$ 式中$P_m$是投影到$M$本征空间,本征值为$m$的投影算符。测量的可能结果与可观测量的本征值$m$相关。当测量$|\psi\rangle$时,得到测量结果$m$的概率为 $$ p(m)=\left\langle\psi\left|P_{m}\right| \psi\right\rangle $$ 得到测量结果$m$后,量子体系的态立刻变为 $$ \frac{P_{m}|\psi\rangle}{\sqrt{p(m)}} $$
对Heisenberg不确定性原理的正确理解是如果我们制备大量处于相同态的量子体系,$|\psi\rangle$,然后对其中的一些系统进行$C$测量,对另外一些系统进行$D$测量。$C$测量结果的标准差$\Delta C$乘上$D$测量结果的标准差$\Delta D$将会满足上式。
假设一个量子体系是一组态$|\psi_i \rangle$中的一个。$i$是下标,对应概率$p_i$。我们称$\lbrace p_i,|\psi_i\rangle\rbrace$纯态系综。该系统的密度算符定义为 $$ \rho \equiv \sum_{i} p_{i}\left|\psi_{i}\right\rangle\left\langle\psi_{i}\right| $$ 量子力学定理用密度矩阵表述 $$ \rho=\sum_{i} p_{i}\left|\psi_{i}\right\rangle\langle\psi_{i}|\stackrel{U}{\longrightarrow} \sum_{i} p_{i} U| \psi_{i}\rangle\langle\psi_{i}| U^{\dagger}=U \rho U^{\dagger} $$
由于
-
对于任意一个孤立的物理体系而言,都有一个与之对应,可以定义内积的复矢量空间,即Hilbert空间。该空间被称为这个系统的态空间。这个体系可以被作用在它的态空间上的密度算符完全描述。密度算符是迹为1的正定算符。
-
封闭量子体系的演化用酉变换描述。也就是说,$t_1$时刻系统的$\rho$态与$t_2$时刻系统的$\rho'$态通过一个仅依赖于时间$t_1$,$t_2$的酉算符进行关联 $$ \rho'=U\rho U^\dagger $$
-
量子测量通过测量算符集$\left\lbrace M_{m}\right\rbrace$描述。它们是作用在正在被测量的态空间上的算符。下标$m$代表实验中可能出现的测量结果。如果在测量前一个时刻量子体系的状态为$\rho$,那么测量结果$m$的出现概率为 $$ p(m)=\text{tr}(M^\dagger_mM_m\rho) $$ 测量之后的量子态为 $$ \frac{M_m\rho M_m^\dagger}{\text{tr}(M^\dagger_mM_m\rho)} $$ 测量算符满足完备性条件 $$ \sum_{m} M_{m}^{\dagger} M_{m}=I $$
-
复合物理体系的态空间是子系统态空间的张量积
纯态 $$ \rho=|\psi\rangle\langle\psi| $$ 否则为混态
判断标准
纯态 $$ \text{tr}(\rho^2)=1 $$ 混态 $$ \text{tr}(\rho^2)<1 $$ 判定密度算符
-
$\rho$ 的迹为1 -
$\rho$ 为正定算符
当且仅当$|\vec{r}|=1$时为纯态
假设$|\psi\rangle$是复合体系$AB$的一个纯态,那么存在$A$中正交态$|i_A\rangle$和$B$中正交态$|i_B\rangle$满足 $$ |\psi\rangle=\sum_{i} \lambda_{i}\left|i_{A}\right\rangle\left|i_{B}\right\rangle $$ 式中$|\lambda_i\rangle$为满足$\sum_{i} \lambda_{i}^{2}=1$的非负实数,被称为Schmidt系数
通过这个结果我们可以发现$\rho^{A}=\sum_{i} \lambda_{i}^{2}\left|i_{A}\right\rangle\left\langle i_{A}\right|$,而$\rho^{B}=\sum_{i} \lambda_{i}^{2}\left|i_{B}\right\rangle\left\langle i_{B}\right|$。因此$\rho^A$和$\rho^B$的本征值相同。
对于量子体系$A$中一个给定的态$\rho^A$,我们可以引入另一个系统$R$,并且对联合体系
Schmidt分解与态纯化
纯化体系$A$中的混态的过程是定义一个在$A$中Schmidt基对角化,Schmidt系数是被纯化的态的密度算符本征值的平方根的纯态。

Alice 和 Bob 同时随机对 Charlie制备的两粒子进行两种不同测量中的一种,所得结果表示方式如图。我们现在考察$QS + RS + RT − QT$。注意到 $$ QS + RS + RT − QT = (Q + R)S + (R − Q)T. $$ 因为$R,Q=\pm 1$,所以要么$(Q + R)S=0$,要么$(R − Q)T=0$。所以$QS + RS + RT − QT=\pm2$
假设测量之前系统处于$Q = q, R = r, S = s, T = t$ 的概率为$p(q, r, s, t)$,那么 $$ \begin{aligned} \mathbf{E}(Q S+R S+R T-Q T) &=\sum_{q r s t} p(q, r, s, t)(q s+r s+r t-q t) \\ & \leq \sum_{q r s t} p(q, r, s, t) \times 2 \\ &=2 \end{aligned} $$ 同时 $$ \begin{aligned} \mathbf{E}(Q S+R S+R T-Q T)=& \sum_{q r s t} p(q, r, s, t) q s+\sum p(q, r, s, t) r s \\ &+\sum_{q r s t} p(q, r, s, t) r t-\sum_{q r s t} p(q, r, s, t) q t \\ =& \mathbf{E}(Q S)+\mathbf{E}(R S)+\mathbf{E}(R T)-\mathbf{E}(Q T) \end{aligned} $$ 所以,我们得到 Bell 不等式 $$ \mathbf{E}(Q S)+\mathbf{E}(R S)+\mathbf{E}(R T)-\mathbf{E}(Q T) \leq 2 $$ 这个结果也叫CHSH不等式
考虑如下两比特态 $$ |\psi\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}} $$ 如果我们对该态测量$\vec{v} \cdot \vec{\sigma}$,那么如果第一个比特测量结果为$+1$,则第二个比特测量结果为$-1$,反之亦然。
现在考虑如下情形:
Charlie 制备了两比特量子体系 $$ |\psi\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}} $$ Alice拿到第一个量子比特,Bob拿到第二个量子比特,他们进行如下测量 $$ \begin{aligned} Q &=Z_{1} & & S=\frac{-Z_{2}-X_{2}}{\sqrt{2}} \\ R &=X_{1} & & T=\frac{Z_{2}-X_{2}}{\sqrt{2}} \end{aligned} $$ 经过简单计算可得 $$ \langle Q S\rangle=\frac{1}{\sqrt{2}} ;\langle R S\rangle=\frac{1}{\sqrt{2}} ;\langle R T\rangle=\frac{1}{\sqrt{2}} ;\langle Q T\rangle=-\frac{1}{\sqrt{2}} $$ 因此 $$ \langle Q S\rangle+\langle R S\rangle+\langle R T\rangle-\langle Q T\rangle= 2 \sqrt{2} $$
并不满足CHSH不等式。所以EPR实验的两个假设当中至少有一个错误
- 实在论:物理属性$P_{Q}, P_{R}, P_{S}, P_{T}$与观测无关地决定了Q, R, S, T的值
- 定域性:Alice的测量不影响Bob的测量
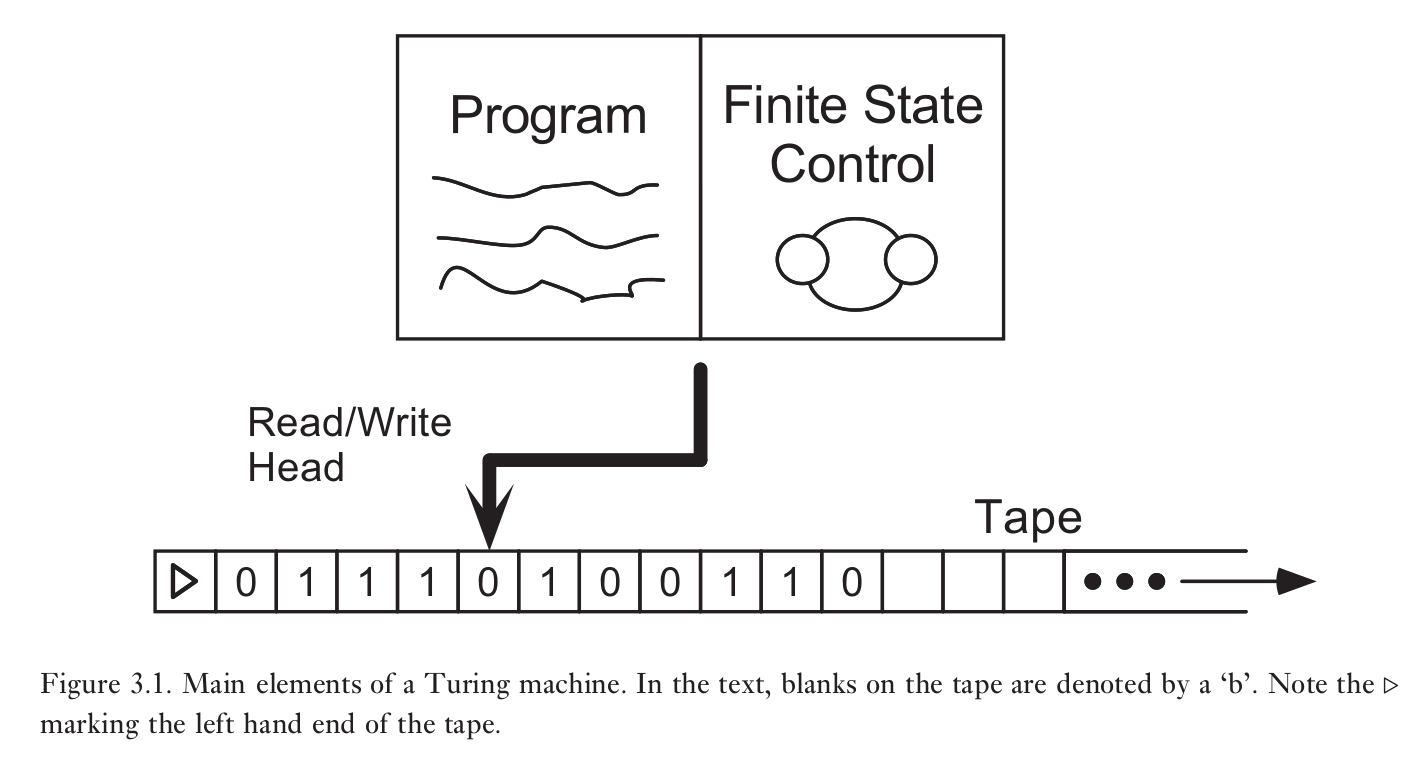
图灵机有四个主要组成部分
-
有限状态控制
图灵机的有限状态控制由一组有限的内部状态,$q_1,\cdots,q_m$组成。除此之外还有两个特殊的态$q_s,q_h$,分别叫做开始状态和结束状态。计算开始时,图灵机处在开始状态$q_s$,实施计算使得图灵机的内部状态发生改变,结束时变为$q_h$,意味着计算完成。
-
磁带
图灵机的磁带单边无限。它由无限个磁带方块序列组成,编号为$0,1,2,3.\cdots$。每个块包含着某个包含有限个分立符号字母表$\Gamma$中的一个字符。
-
磁带读写指针
-
程序
图灵机的程序是一个$<q,x,q',x',s>$格式命令行的有限有序列表。q 是图灵机的内部状态,x 是从磁带读取的数据,q ' 为图灵机执行完该条命令后变成内部状态,x' 为写入磁带的内容,s 为磁头移动
通用图灵机
固定程序和内部状态,只有磁带的初始内容可变的图灵机可以模拟任何图灵机,与该图灵机所以时间为多项式的关系。
一组确定的门可以用来计算任意函数$f:{0,1}^n\to{0,1}^m$
分析计算问题取决于以下三个基本问题的答案
- 什么是计算问题?这里讨论决定性问题。
- 怎样确定算法解决给定的计算问题?什么算法可以用,有没有通用算法,怎样确定算法按照预期进行
- 解决给定的计算问题所需的最少资源是多少?时间,空间,能量
O:上界
对于给定的n比特的输入,如果能够在n的多项式资源内解决,那么这个问题就是简单的,否则就是困难的。
任何计算模型都可以被概率图灵机模拟,基本操作数最多为多项式增加。
形式语言是一个字母表上的某些有限长字符串的集合。一个形式语言可以包含无限多个字符串。决定性问题可以用形式语言编码
如果一个问题可以在有限k的$TIME(n^k)$时间内解决,那么就称之为多项式可解。$TIME(n^k)$中的所有语言的集合记为P
如果存在图灵机M具有以下性质,那么语言L属于NP
- 如果$x\in L$,那么存在见证字符串w使得M从状态$x-blank-w$开始,并且在$|x|$的多项式时间内停止于$q_Y$状态。
- 如果$x\notin L$,那么对于任意尝试作为见证的字符串w,都有M从状态$x-blank-w$开始,在$|x|$的多项式时间内停止于$q_N$状态。
类似地,可以定义coNP,将上述两条件交换
NP完全问题:最难的NP问题,若NP完全问题有多项式时间解,则P=NP
问题约化
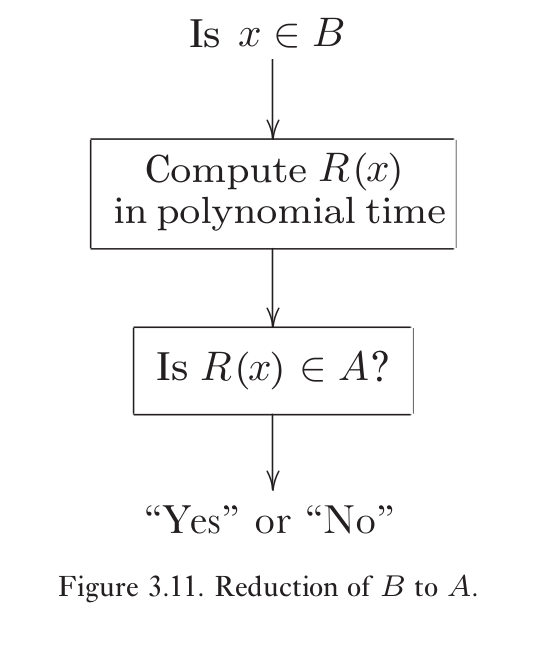
L:对数时间复杂度
P:多项式时间复杂度
NP:多项式时间内验证
PSPACE:多项式空间
EXP:指数时间复杂度 $$ \mathbf{L} \subseteq \mathbf{P} \subseteq \mathbf{N P} \subseteq \mathbf{P S P A C E} \subseteq \mathbf{E X P} $$ 尽管该关系被广泛认为是严格的,但没有任何一个式子被证明是严格成立的。不过由时间分层定理可知,$P$是$EXP$的真子集。因此上式至少有一个式子严格成立
时间分层定理:$TIME(f(n))$是$TIME(f(n)\log^2(f(n)))$的真子集
空间分层定理:$SPACE(f(n))$是$SPACE(f(n)\log(f(n)))$的真子集
MAXSNP:可以通过近似方法有效验证的问题集合
BPP(bounded-error probabilistic time): 所以具有以下特性的语言L集合:存在概率图灵机M,如果$x\in L$,那么M有至少$3/4$的概率接受x,如果$x\notin L$,那么M有至少$3/4$的概率拒绝x。这里$3/4$可任选大于$1/2$的数
如果一个计算机擦除了一比特信息,那么释放到环境中的能量至少为$k_B T\ln 2$。$k_B$为玻耳兹曼常数,$T$为计算机环境温度
如果一个计算机擦除了一比特信息,那么环境的熵增至少为$k_B\ln 2$。$k_B$为玻耳兹曼常数
Landauer原则给出了能量消耗的下限,如果所有计算都是可逆的,那么几乎可以不消耗能量。此时能量损耗主要来自于其他物理过程,例如噪声。
这里给出两种可逆通用门
利用撞球模型可以制造Fredkin门
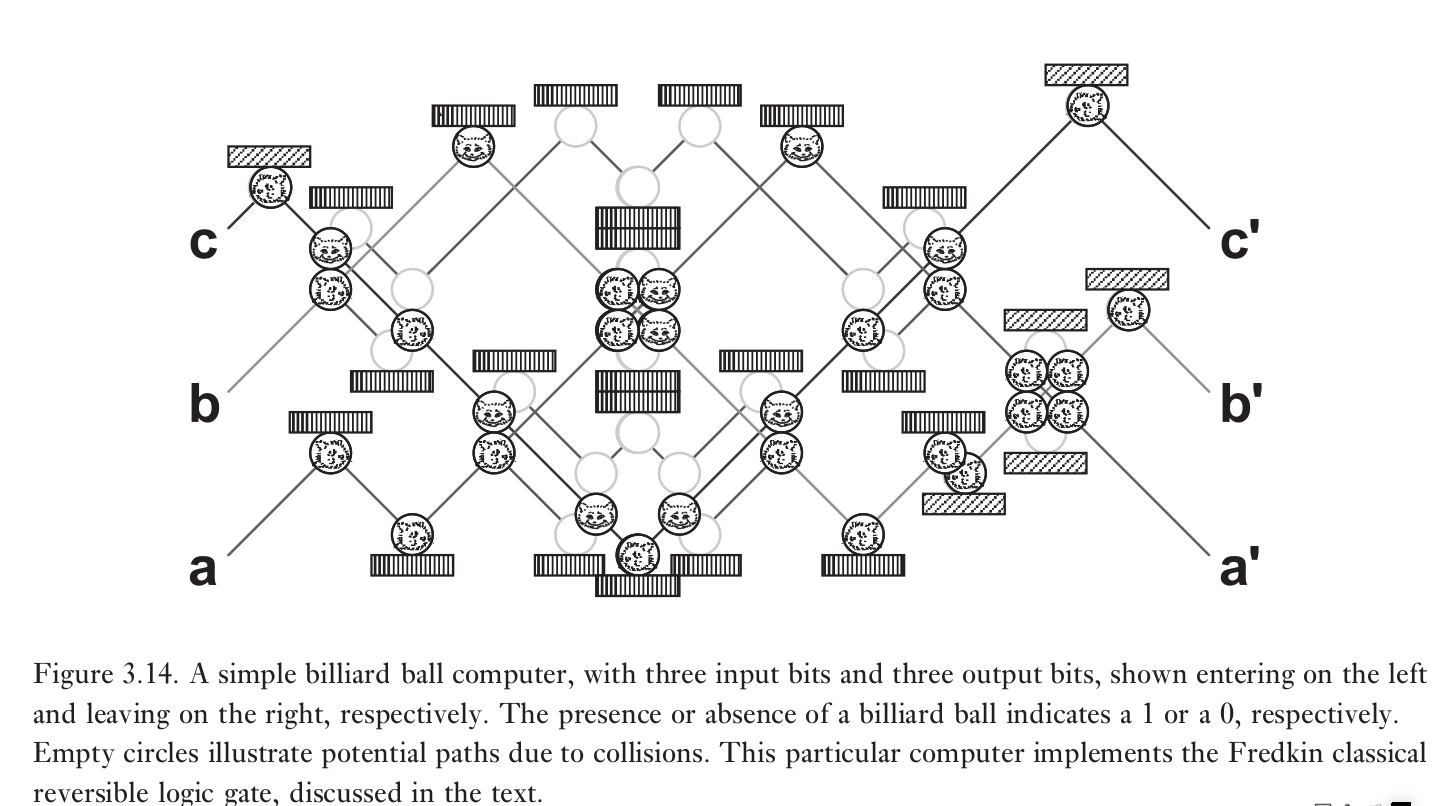
真值表如下
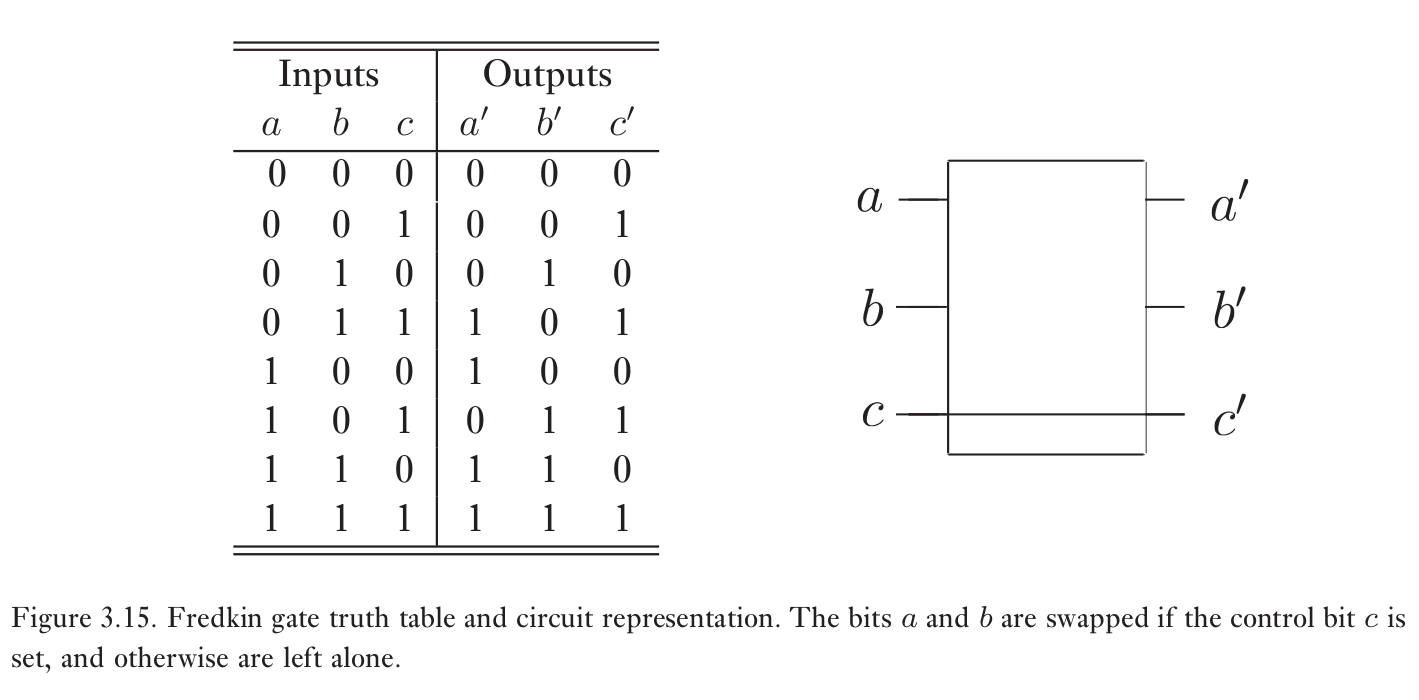
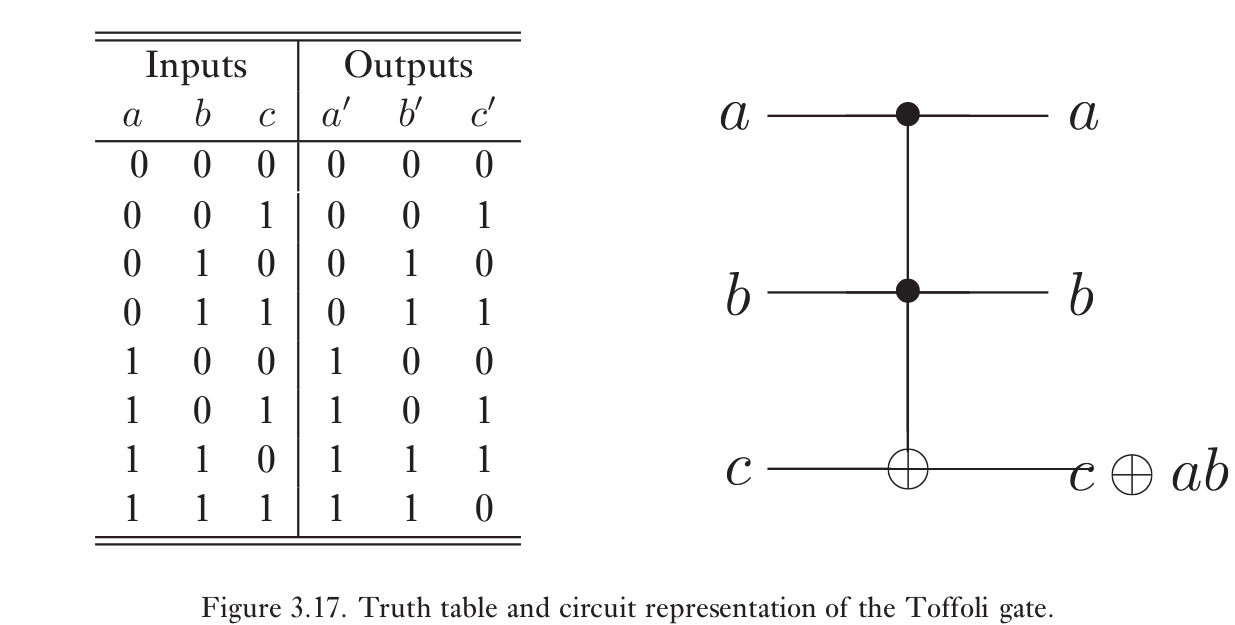
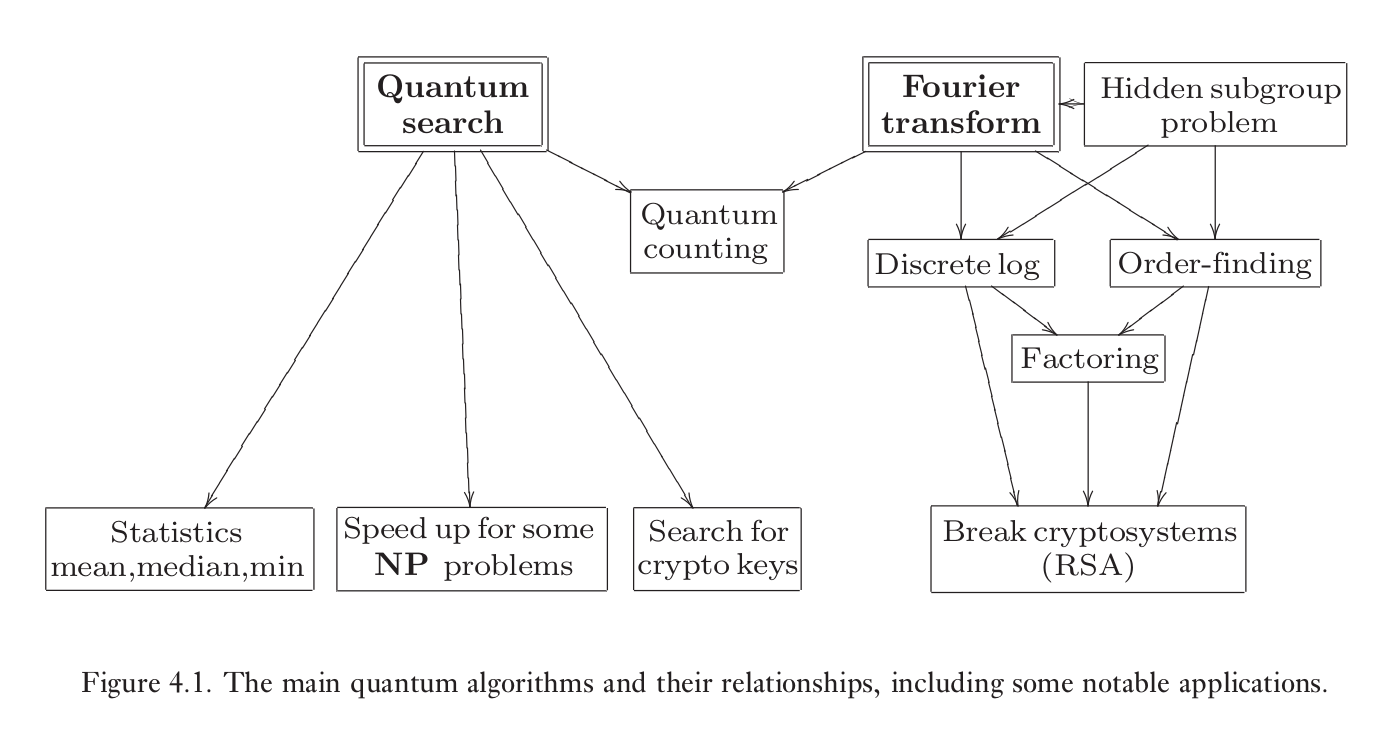
Pauli矩阵 $$ X \equiv\left[\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right] ; \quad Y \equiv\left[\begin{array}{cc}{0} & {-i} \\ {i} & {0}\end{array}\right] ; \quad Z \equiv\left[\begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right] $$
Hadamared门,相位门,$\pi/8$门
关于$\hat{x},\hat{y},\hat{z}$的旋转算符 $$ \begin{array}{l}{R_{x}(\theta) \equiv e^{-i \theta X / 2}=\cos \frac{\theta}{2} I-i \sin \frac{\theta}{2} X=\left[\begin{array}{cc}{\cos \frac{\theta}{2}} & {-i \sin \frac{\theta}{2}} \\ {-i \sin \frac{\theta}{2}} & {\cos \frac{\theta}{2}}\end{array}\right]} \\ {R_{y}(\theta) \equiv e^{-i \theta Y / 2}=\cos \frac{\theta}{2} I-i \sin \frac{\theta}{2} Y=\left[\begin{array}{cc}{\cos \frac{\theta}{2}} & {-\sin \frac{\theta}{2}} \\ {\sin \frac{\theta}{2}} & {\cos \frac{\theta}{2}}\end{array}\right]} \\ {R_{z}(\theta)} {\equiv e^{-i \theta Z / 2}=\cos \frac{\theta}{2} I-i \sin \frac{\theta}{2} Z=\left[\begin{array}{cc}{e^{-i \theta / 2}} & {0} \\ {0} & {e^{i \theta / 2}}\end{array}\right]}\end{array} $$ 上式由 $$ \exp (i A x)=\cos (x) I+i \sin (x) A $$ 可得。 $$ R_{\hat{n}}(\theta) \equiv \exp (-i \theta \hat{n} \cdot \vec{\sigma} / 2)=\cos \left(\frac{\theta}{2}\right) I-i \sin \left(\frac{\theta}{2}\right)\left(n_{x} X+n_{y} Y+n_{z} Z\right) $$ 任意单量子比特算符可以写为如下形式 $$ U=\exp (i \alpha) R_{\hat{n}}(\theta) $$
若U为单比特酉变换门,则存在满足$ABC=I$的单量子比特酉算符使得
$$
U=e^{i \alpha} A X B X C
$$
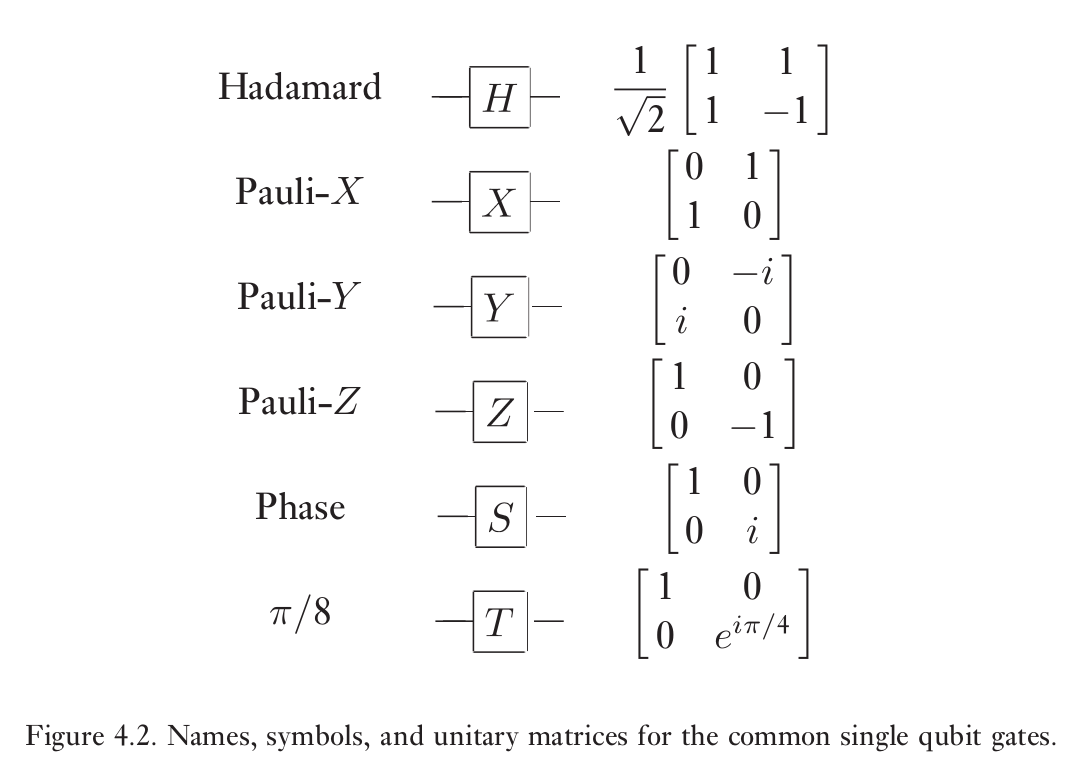
受控操作的一个典型为受控非 C-NOT
$$
|c\rangle|t\rangle \rightarrow|c\rangle|t \oplus c\rangle
$$
在计算基$|control,target\rangle$下,CNOT的矩阵表示为
$$
\left[\begin{array}{llll}{1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {0} & {1} \\ {0} & {0} & {1} & {0}\end{array}\right]
$$
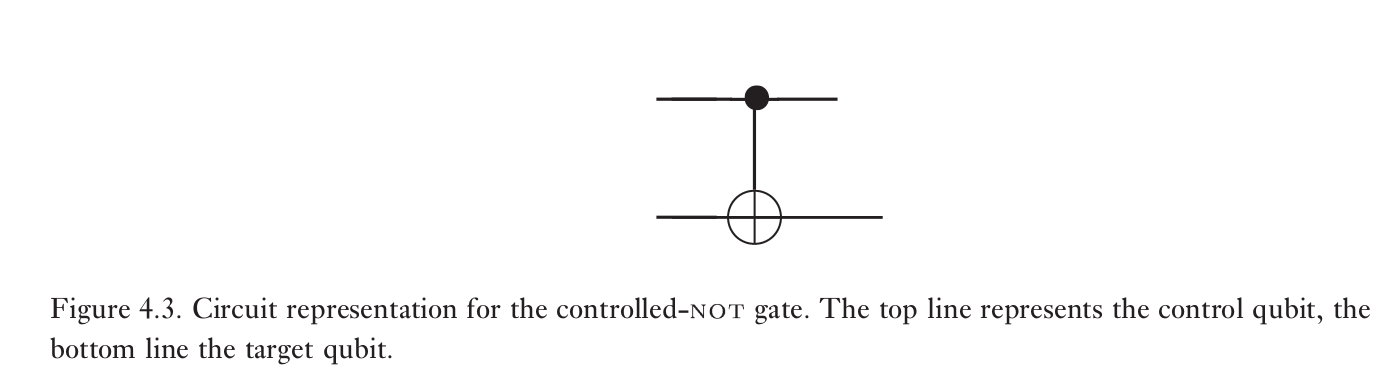
类似的,控制U变换
$$
|c\rangle|t\rangle \rightarrow|c\rangle U^{c}|t\rangle
$$
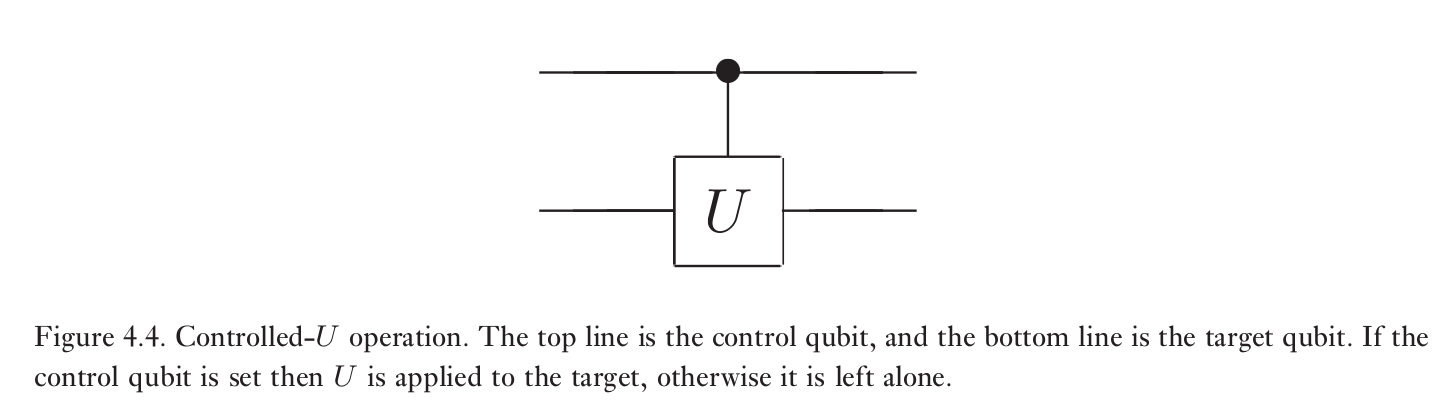
仅需使用单比特操作门和CNOT门
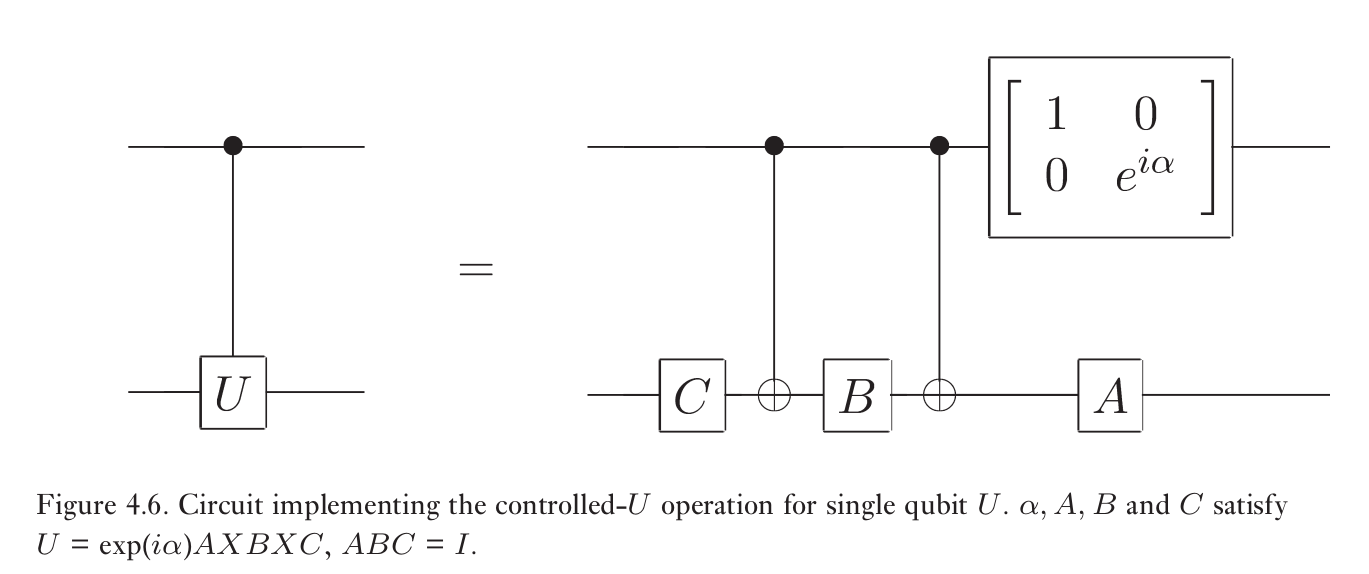
该过程基于分解 $$ U=e^{i \alpha} A X B X C $$
- 实现受控相位变换 $$ |00\rangle \rightarrow|00\rangle, \quad|01\rangle \rightarrow|01\rangle, \quad|10\rangle \rightarrow e^{i \alpha}|10\rangle, \quad|11\rangle \rightarrow e^{i \alpha}|11\rangle $$
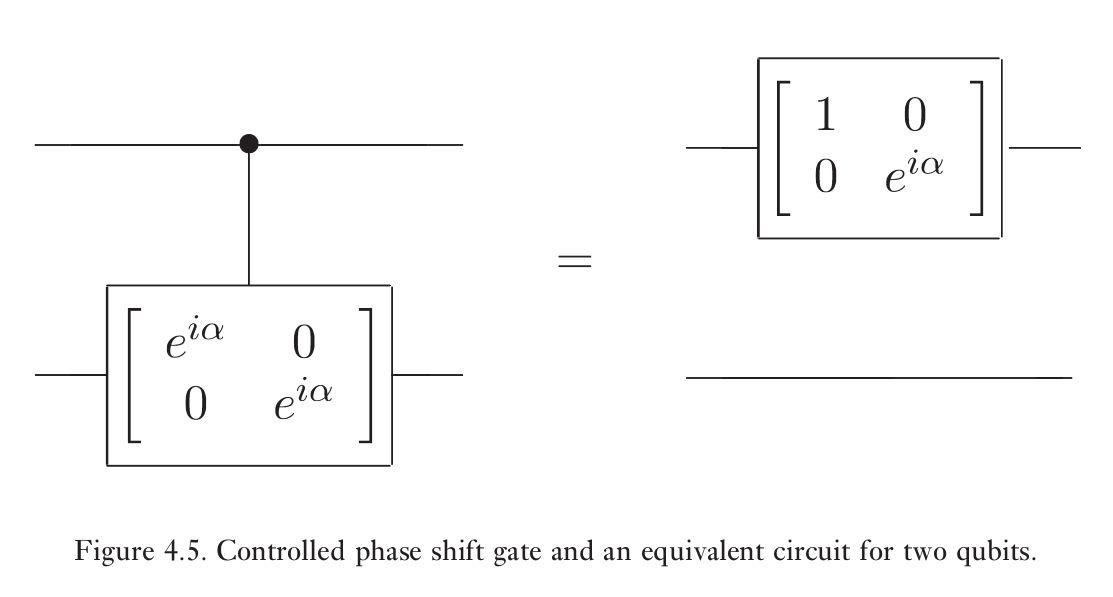
-
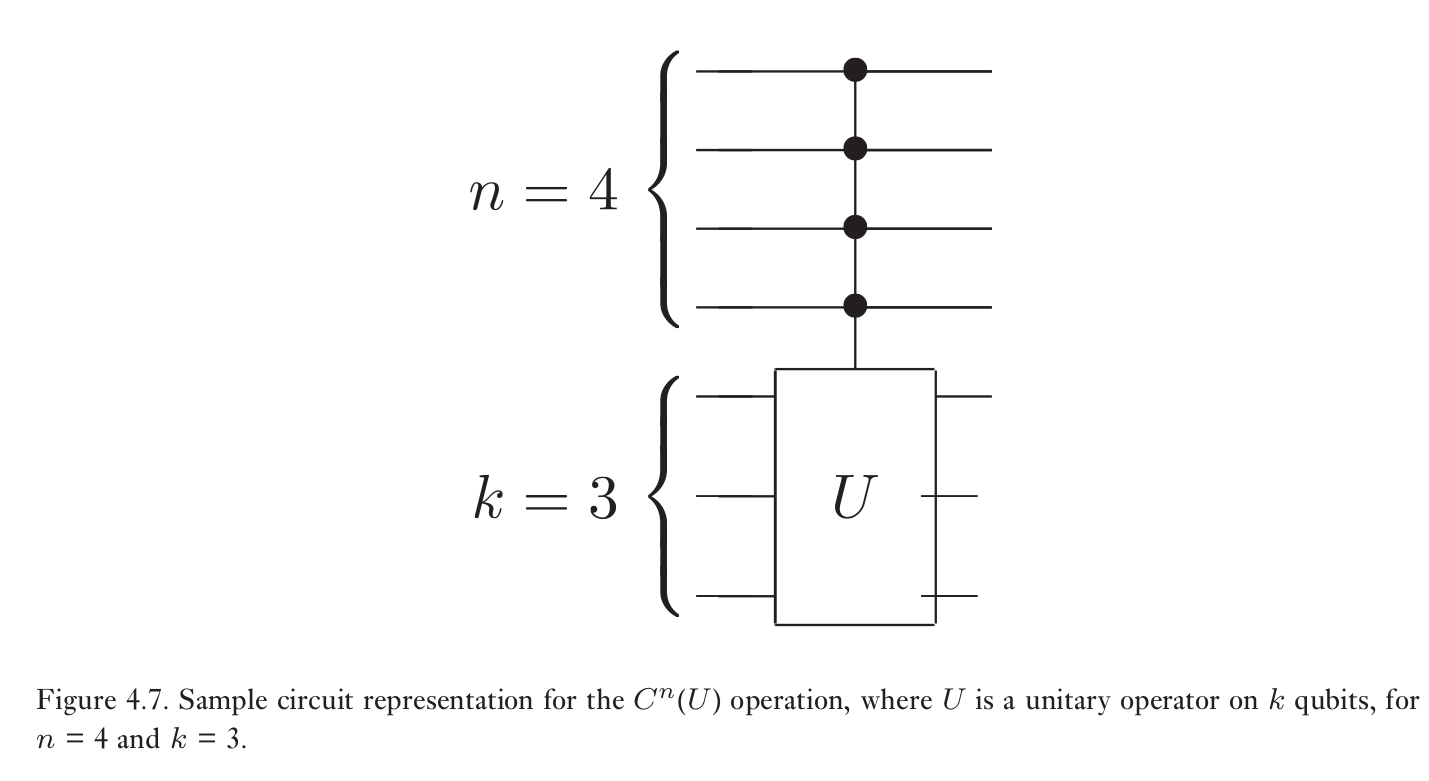
实现受控U变换
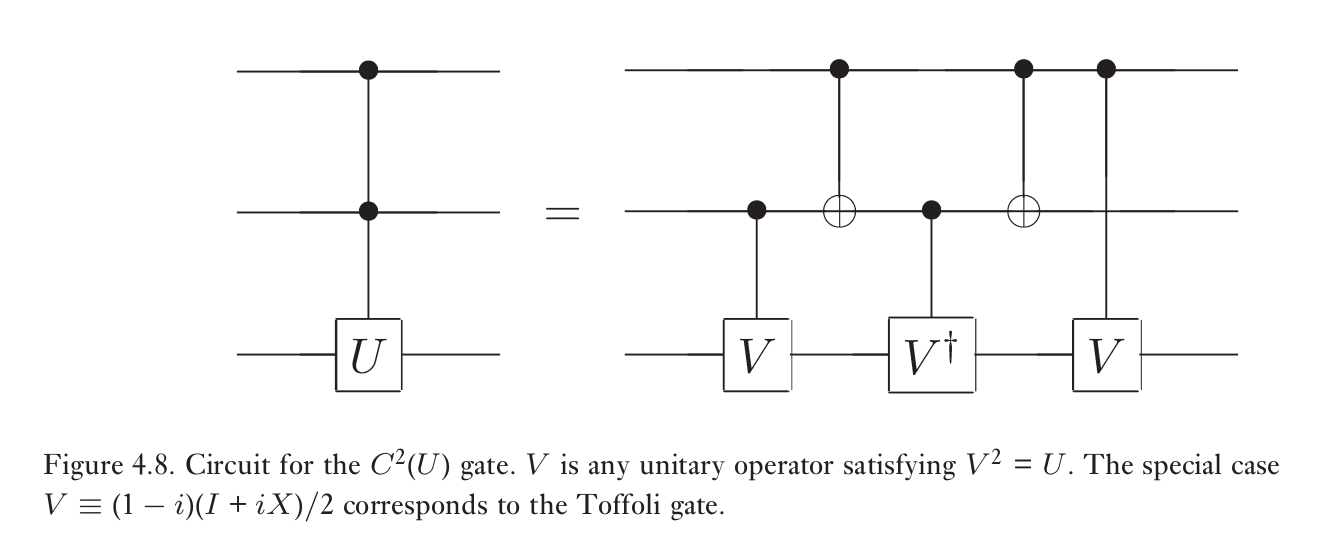
任意酉变换可以用Hadamard,相位,CNOT和$\pi/8$门进行任意精度要求的近似
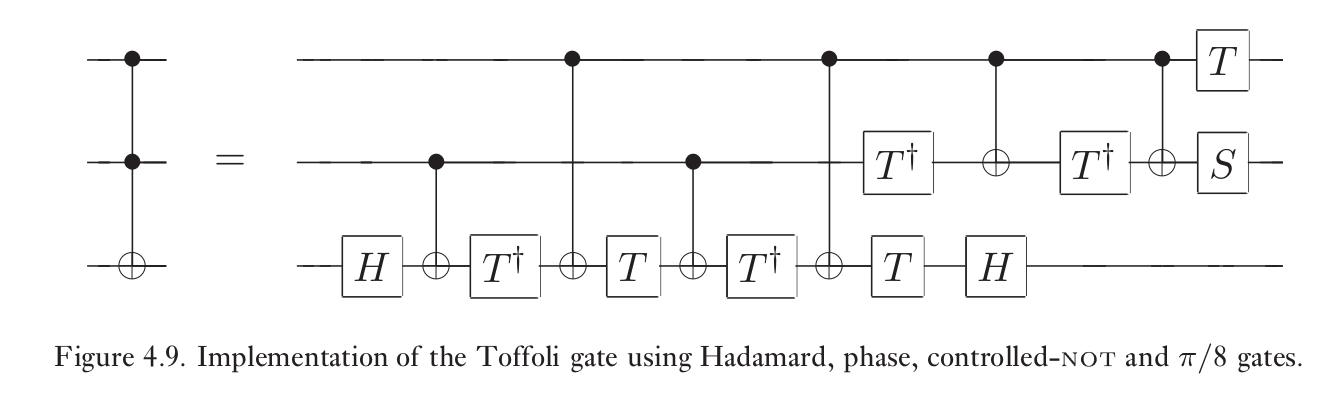
几乎无可质疑,量子线路中的最后一个元素便是测量。我们用表的符号表示测量基上的投影测量
量子线路中有两条重要的原理
- 经典条件操作可以用量子条件操作替代:推迟测量原理:测量总是可以从量子线路的中间过程移到线路的末尾;如果线路的任何过程用到测量结果,那么经典受控操作可以用量子受控操作替代
- 隐测量原理:不失一般性,任何未封端的量子线(未被测量的量子比特)可以假设被测量。
一般认为测量是一个不可逆的过程,它破坏了量子信息,代之以经典信息。然而在一些精心设计的情况下,这也不是必然发生的。测量要可逆,它必须不揭示被测量子态的任何信息。
测量一般默认在计算基下测量,但我们经常需要在其他基下测量,此时我们只需要进行一个酉变换将我们所需的基变换到计算基下即可。例如
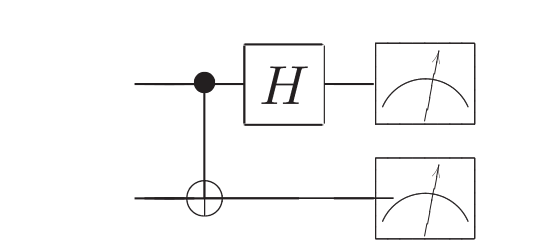
进行Bell态基矢下的测量
当被测量的量子比特是控制量子比特时,测量和量子门对易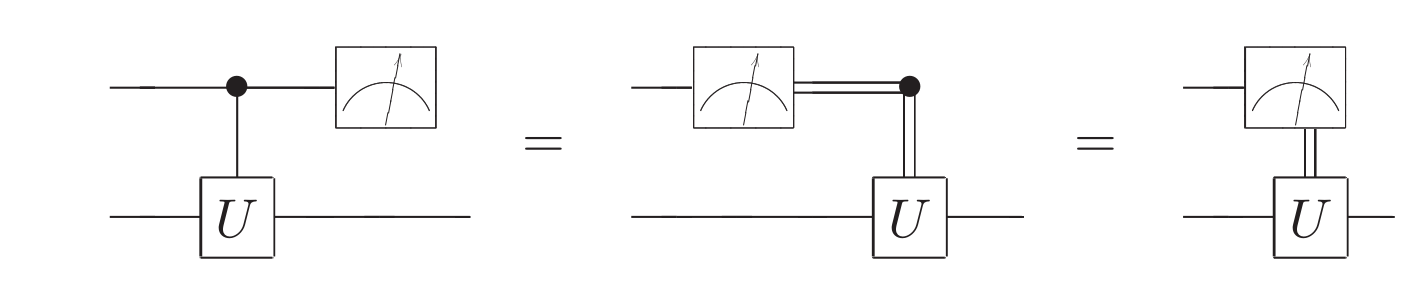
如果用一组门的量子线路可以以任意精度近似任意的酉运算,则称这组门对量子计算是通用的。
考虑一个作用在d维希尔伯特空间上的酉矩阵U。在本节,我们将解释怎样将U分解为二级酉矩阵的乘积。二级酉矩阵即只对两个或更少向量元素有着非平凡作用的酉矩阵。
以三阶酉矩阵为例 $$ U=\left[\begin{array}{lll}{a} & {d} & {g} \\ {b} & {e} & {h} \\ {c} & {f} & {j}\end{array}\right] $$ 我们将寻找二级酉矩阵$U_{1}, \ldots, U_{3}$使得 $$ U_{3} U_{2} U_{1} U=I $$ 因此 $$ U=U_{1}^{\dagger} U_{2}^{\dagger} U_{3}^{\dagger} $$ 因为$U_{1},U_{2},U_{3}$都是二级酉矩阵,$U_{1}^{\dagger} ,U_{2}^{\dagger} ,U_{3}^{\dagger}$也为二级酉矩阵
下面开始构建这些矩阵
如果$b=0$,那么令 $$ U_{1} \equiv\left[\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right] $$ 如果$b\neq 0$,那么令 $$ U _{1} \equiv \left[ \begin{array}{ccc} \frac{a^ *}{\sqrt{|a|^2+|b|^2}} & \frac{b^ *}{\sqrt{|a|^2+|b|^2}} & 0 \\ \frac{b}{\sqrt{|a|^2+|b|^2}} & \frac{-a}{\sqrt{|a|^{2}+|b|^{2}}} & 0 \\ 0 & 0 & 1 \end{array} \right] $$
我们得到
类似的,如果$c'=0$,那么令
如果$c'\neq0$,那么令
这样我们得到
因为$U,U_1,U_2$为酉矩阵,所以$U_{2} U_{1} U$也为酉矩阵,所以$d^{\prime \prime}=g^{\prime \prime}=0$
最后令
更一般的,对于d维的情况,类似的,我们也可以找到二级酉矩阵$U_{1}, \ldots, U_{d-1}$使得左上角的元素为1,第一行以及第一列的其他元素均为0。对于d-1维矩阵重复该过程,最终我们可以得到任意$d\times d$酉矩阵可以写为
这里$V_i$是二级酉矩阵并且$k \leq(d-1)+(d-2)+\cdots+1=d(d-1)/2$
上述结果的一个推论为n比特的任何一个酉矩阵可以写成最多$2^{n-1}\left(2^{n}-1\right)$个二级酉矩阵的乘积
单量子比特门和CNOT门组合在一起可以用来实现任意一个n量子比特的态空间中二级酉操作。
假设U是n量子比特量子计算机上的一个二级酉矩阵。假设U非平凡地作用在计算基$|s\rangle$和$|t\rangle$张成的空间上。
其中$s=s_{1} \dots s_{n}$,$t=t_{1} \dots t_{n}$是s和t的二进制展开。令$\tilde{U}$为U的非平凡$2\times 2$酉子矩阵;$\tilde{U}$可以认为是单个量子比特的酉算符。
我们将通过格雷码,仅利用单量子比特门和CNOT门构建线路实现U
令$g_1$到$g_m$为连接s到t的格雷码,$g_1=s$,$g_m=t$
实施U的过程为依次进行操作使得$|g_{1}\rangle \rightarrow|g_{2}\rangle \rightarrow \ldots \rightarrow|g_{m-1}\rangle$,然后实施$C-\tilde{U}$操作,目标比特为$g_{m-1}$和$g_m$不同的单个比特,然后逆向操作第一步,$\left|g_{m-1}\right\rangle \rightarrow\left|g_{m-2}\right\rangle \rightarrow \ldots \rightarrow\left|g_{1}\right\rangle$
例如我们想要实现如下二级酉变换 $$ U=\left[\begin{array}{llllllll}{a} & {0} & {0} & {0} & {0} & {0} & {0} & {c} \\ {0} & {1} & {0} & {0} & {0} & {0} & {0} & {0} \\ {0} & {0} & {1} & {0} & {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {1} & {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {1} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0} & {1} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} & {1} & {0} \\ {b} & {0} & {0} & {0} & {0} & {0} & {0} & {d}\end{array}\right] $$ 这里a,b,c,d为任意复数使得$\tilde{U} \equiv\left[\begin{array}{ll}{a} & {c} \\ {b} & {d}\end{array}\right]$为一个酉矩阵
注意到U只对$|000\rangle$和$|111\rangle$有着非平凡的作用,格雷码如下 $$ \begin{array}{ccc}{A} & {B} & {C} \\ {0} & {0} & {0} \\ {0} & {0} & {1} \\ {0} & {1} & {1} \\ {1} & {1} & {1}\end{array} $$ 线路图如下
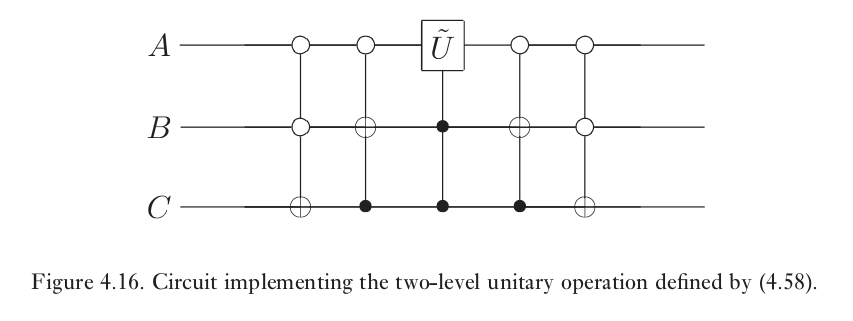
该方法用于n量子比特的任意酉操作需要$O(n^24^n)$单量子比特门和CNOT门
有接近最优的方案需要指数的门
当使用V代替U时定义误差如下 $$ E(U, V) \equiv \max _{|\psi\rangle} \Vert(U-V)|\psi\rangle \Vert $$ 如果$E(U,V)$足够小,那么任何作用在态$V|\psi\rangle$上的测量都将给出与作用在态$U|\psi\rangle$上近似相同的测量结果统计。 $$ \left|P _{U}-P _{V}\right| \leq 2 E(U, V) $$