You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Problem: Tsallis Divergence is not lower-bounded, hence minimization will leads towards negative infinity.
Definition The Tsallis Divergence is defined as :
where if alpha approaches one then this approaches the Kullback-Leibler. This can be proven by using L Hopital rule (since bottom and top evaluate to zero then we satisfy L Hopital assumption) and showing that
Implementation: I'm putting in the constraint that the integral should match. I'm use mask value of 1e-12 to g(x) from the division of f(x) with g(x) and set the ratio (f(x)/g(x)) to zero if g(x) < 1e-12.
Choosing Alpha
Choosing alpha to be very tight, 1.0000001, after 13 iterations with trust-constraint, it got to -4.0983e+04 Tsallis and KL value of infinity (model density is negative somwhere).
Choosing alpha to be 1.0001, then I see a lower-bound. I also see this when I plot it. After 84 iterations with trust-constraint, Tsallis value converged to +2.7715e-02 with KL value of 0.0415.
Choosing alpha < 1, we get that it is approaching logarithm from below and hence will not be lower-bounded, turst-constr gives -infinity as objective value.
Choosing 1.00001 after 157 iterations, trust constraint region method seems to convergence to Tsallis value of -0.145, and KL value of 0.069285
Reference
[1] - Paul "Information Theory, the shape function and the Hirshfield atom"
[2] - Farnaz "Hirshfield partioning from non-extensive entropies"
Going to do: I'm going to run these alpha for longer periods of time.
Problem: Tsallis Divergence is not lower-bounded, hence minimization will leads towards negative infinity.
Definition The Tsallis Divergence is defined as :
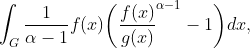
where if alpha approaches one then this approaches the Kullback-Leibler. This can be proven by using L Hopital rule (since bottom and top evaluate to zero then we satisfy L Hopital assumption) and showing that

Plotting this, it does seem to approach it.
Implementation: I'm putting in the constraint that the integral should match. I'm use mask value of 1e-12 to g(x) from the division of f(x) with g(x) and set the ratio (f(x)/g(x)) to zero if g(x) < 1e-12.
Choosing Alpha
Reference
[1] - Paul "Information Theory, the shape function and the Hirshfield atom"
[2] - Farnaz "Hirshfield partioning from non-extensive entropies"
Going to do: I'm going to run these alpha for longer periods of time.
@FarnazH @PaulWAyers
The text was updated successfully, but these errors were encountered: