Skip to content

Latest commit

 

History

History
270 lines (228 loc) · 7.94 KB

README.md

File metadata and controls

270 lines (228 loc) · 7.94 KB

1168. 水资源分配优化

English Version

题目描述

村里面一共有 n 栋房子。我们希望通过建造水井和铺设管道来为所有房子供水。

对于每个房子 i，我们有两种可选的供水方案：一种是直接在房子内建造水井，成本为 wells[i - 1] （注意 -1 ，因为 索引从0开始 ）；另一种是从另一口井铺设管道引水，数组 pipes 给出了在房子间铺设管道的成本，其中每个 pipes[j] = [house1j, house2j, costj] 代表用管道将 house1j 和 house2j连接在一起的成本。连接是双向的。

请返回 为所有房子都供水的最低总成本 。

 

示例 1：

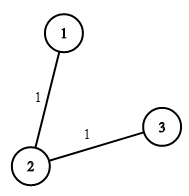
输入：n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
输出：3
解释： 
上图展示了铺设管道连接房屋的成本。
最好的策略是在第一个房子里建造水井（成本为 1），然后将其他房子铺设管道连起来（成本为 2），所以总成本为 3。

示例 2：

输入：n = 2, wells = [1,1], pipes = [[1,2,1]]
输出：2
解释：我们可以用以下三种方法中的一种来提供低成本的水:
选项1:
在1号房子里面建一口井，成本为1
在房子2内建造井，成本为1
总成本是2。
选项2:
在1号房子里面建一口井，成本为1
-花费1连接房子2和房子1。
总成本是2。
选项3:
在房子2内建造井，成本为1
-花费1连接房子1和房子2。
总成本是2。
注意，我们可以用cost 1或cost 2连接房子1和房子2，但我们总是选择最便宜的选项。

 

提示：

  • 2 <= n <= 104
  • wells.length == n
  • 0 <= wells[i] <= 105
  • 1 <= pipes.length <= 104
  • pipes[j].length == 3
  • 1 <= house1j, house2j <= n
  • 0 <= costj <= 105
  • house1j != house2j

解法

方法一：Kruskal 算法（最小生成树）

我们假设有一个水井编号为 $0$，那么我们可以将每个房子与水井 $0$ 之间的连通性看作是一条边，每条边的权值为该房子建造水井的成本。同时，我们将每个房子之间的连通性也看作是一条边，每条边的权值为铺设管道的成本。这样一来，我们就可以将本题转化成求一张无向图的最小生成树的问题。

我们可以使用 Kruskal 算法求出无向图的最小生成树。我们先把水井 $0$ 与房子之间的一条边加入 $pipes$ 数组中，然后将 $pipes$ 数组按照边权值从小到大排序。随后，我们遍历每一条边，如果这条边连接了不同的连通分量，我们就选用这条边，并将对应连通分量合并。如果当前的连通分量恰好为 $1$，那么我们就找到了最小生成树，此时的答案即为当前边权值，我们将其返回即可。

时间复杂度 $O((m + n) \times \log (m + n))$，空间复杂度 $O(m + n)$。其中 $m$ 和 $n$ 分别是 $pipes$ 数组和 $wells$ 数组的长度。

Python3

class Solution:
    def minCostToSupplyWater(
        self, n: int, wells: List[int], pipes: List[List[int]]
    ) -> int:
        def find(x: int) -> int:
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        for i, w in enumerate(wells, 1):
            pipes.append([0, i, w])
        pipes.sort(key=lambda x: x[2])
        p = list(range(n + 1))
        ans = 0
        for i, j, c in pipes:
            pa, pb = find(i), find(j)
            if pa == pb:
                continue
            p[pa] = pb
            ans += c
            n -= 1
            if n == 0:
                break
        return ans

Java

class Solution {
    private int[] p;

    public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
        var nums = new int[n + pipes.length][0];
        int j = 0;
        for (var pipe : pipes) {
            nums[j++] = pipe;
        }
        for (int i = 0; i < n; ++i) {
            nums[j++] = new int[] {0, i + 1, wells[i]};
        }
        Arrays.sort(nums, (a, b) -> a[2] - b[2]);
        p = new int[n + 1];
        for (int i = 1; i <= n; ++i) {
            p[i] = i;
        }
        int ans = 0;
        for (var x : nums) {
            int pa = find(x[0]), pb = find(x[1]);
            if (pa == pb) {
                continue;
            }
            ans += x[2];
            p[pa] = pb;
            if (--n == 0) {
                break;
            }
        }
        return ans;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    int minCostToSupplyWater(int n, vector<int>& wells, vector<vector<int>>& pipes) {
        for (int i = 0; i < n; ++i) {
            pipes.push_back({0, i + 1, wells[i]});
        }
        sort(pipes.begin(), pipes.end(), [](const vector<int>& a, const vector<int>& b) {
            return a[2] < b[2];
        });
        int p[n + 1];
        iota(p, p + n + 1, 0);
        function<int(int)> find = [&](int x) {
            if (p[x] != x) {
                p[x] = find(p[x]);
            }
            return p[x];
        };
        int ans = 0;
        for (const auto& x : pipes) {
            int pa = find(x[0]), pb = find(x[1]);
            if (pa == pb) {
                continue;
            }
            p[pa] = pb;
            ans += x[2];
            if (--n == 0) {
                break;
            }
        }
        return ans;
    }
};

Go

func minCostToSupplyWater(n int, wells []int, pipes [][]int) (ans int) {
	for i, w := range wells {
		pipes = append(pipes, []int{0, i + 1, w})
	}
	sort.Slice(pipes, func(i, j int) bool { return pipes[i][2] < pipes[j][2] })
	p := make([]int, n+1)
	for i := range p {
		p[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}

	for _, x := range pipes {
		pa, pb := find(x[0]), find(x[1])
		if pa == pb {
			continue
		}
		p[pa] = pb
		ans += x[2]
		n--
		if n == 0 {
			break
		}
	}
	return
}

TypeScript

function minCostToSupplyWater(
    n: number,
    wells: number[],
    pipes: number[][],
): number {
    for (let i = 0; i < n; ++i) {
        pipes.push([0, i + 1, wells[i]]);
    }
    pipes.sort((a, b) => a[2] - b[2]);
    const p = new Array(n + 1).fill(0).map((_, i) => i);
    const find = (x: number): number => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    let ans = 0;
    for (const [i, j, c] of pipes) {
        const pa = find(i);
        const pb = find(j);
        if (pa === pb) {
            continue;
        }
        p[pa] = pb;
        ans += c;
        if (--n === 0) {
            break;
        }
    }
    return ans;
}

...