Navigation & Localization
Most of the information you come across regarding navigation will be in the form of a pose, which is describes an object's translation and rotation in 3D space with respect to some reference location (this may be the center of the room, another object, or something completely arbitrary). The idea being that with just this information, you can figure out exactly where in the environment an object is and how it is oriented. Depending on your background, you may already be familiar with one of the following notations:
- Euler Notation:
- Position (XYZ)
- Euler Angles (RPY)
- Quaternion Notation:
- Position (XYZ)
- Quaternion (XYZW)
- Matrix Notation:
- Position (XYZ)
- Rotation Matrix (3x3 Matrix)
You may notice that each of these notations are quite similar, and that's because they are. Each notation has a common position or translation component, while their description of the relative rotation is slightly different. The most important thing to realize is that no matter what the notation is used, the fundamental data (that is, a relative translation and rotation) represented by all 3 will be exactly the same.
The translation component of a pose simply represents how far an object is from the reference location. To locate the object relative to the reference location, we simply have to add the object's translation component to the reference's translation component:
x_object = x_reference + x_relative
y_object = y_reference + y_relative
z_object = z_reference + z_relative
If you are using the center of the room as the reference zero location (X=0,Y=0,Z=0), then the translational component of the pose is the objects location.
The rotational component of a pose can vary in notation, but it fundamentally represents the relative rotation from one object to another. The 3 most common representations for a relative rotation are:
- Euler Angles (RPY)
- Uses the classic "Roll", "Pitch", "Yaw" as a description
- Is the most compact way to describe a rotation in 3D space
- Has issues with convention as it must be decoded the same way it is encoded
- Suffers from the gimbal lock problem
- Quaternion (XYZW)
- Defines an axis of rotation (the vector XYZ) and a rotation angle around that (W)
- Can be easily multiplied with another Quaternion to "add" rotations together
- Is the most efficient way to avoid the gimbal lock problem.
- Rotation Matrix (3x3)
- A 3x3 matrix that can be directly multiplied with a vector to rotate it
- Can be easily multiplied with another Rotation Matrix to "add" rotations together
As a reminder, all 3 methods of writing rotation data are comparable, however depending on your application, may not be the best choice.
If you are using the center of the room as the reference zero rotation, then the rotational component of the pose is the objects rotation.
While a pose can be written as a any of the descriptions listed above, the most useful general notation is the 3D Affine Transformation. This transformation consists of a 4x4 matrix that contains the relative rotation matrix and relative translation vector:
R11 R12 R13 X
R21 R22 R23 Y
R31 R32 R33 Z
0 0 0 1
While this transformation will not be discussed in detail, it is good to be aware of the following:
- Multiplying two of these transformations together allows an easy method to chain together relative transformations
- There is an inverse calculation that can be used to easily "undo" or "go backwards" with the relative transformations
This assumes the use of the typical ZYX format used in aerospace and standard ROS types.
For Python:
#!/usr/bin/env python
from math import *
from geometry_msgs.msg import Quaternion, Vector3
def quaternion_to_rpy(q):
if not isinstance(q, Quaternion):
raise TypeError('Input should be a geometry_msgs/Quaternion')
q2sqr = q.y * q.y
t0 = -2.0 * (q2sqr + q.z * q.z) + 1.0
t1 = 2.0 * (q.x * q.y + q.w * q.z)
t2 = -2.0 * (q.x * q.z - q.w * q.y)
t3 = 2.0 * (q.y * q.z + q.w * q.x)
t4 = -2.0 * (q.x * q.x + q2sqr) + 1.0
if(t2 > 1.0):
t2 = 1.0
elif(t2 < -1.0):
t2 = -1.0
roll = atan2(t3, t4)
pitch = asin(t2)
yaw = atan2(t1, t0)
return (roll,pitch,yaw)
def rpy_to_quaternion(roll,pitch,yaw):
t0 = cos(yaw * 0.5);
t1 = sin(yaw * 0.5);
t2 = cos(roll * 0.5);
t3 = sin(roll * 0.5);
t4 = cos(pitch * 0.5);
t5 = sin(pitch * 0.5);
q = Quaternion()
q.w = t2 * t4 * t0 + t3 * t5 * t1;
q.x = t3 * t4 * t0 - t2 * t5 * t1;
q.y = t2 * t5 * t0 + t3 * t4 * t1;
q.z = t2 * t4 * t1 - t3 * t5 * t0;
return qFor C++:
geometry_msgs::Vector3 quaternion_to_rpy(geometry_msgs::Quaternion q) {
geometry_msgs::Vector3 e;
double q2sqr = q.y * q.y;
double t0 = -2.0 * (q2sqr + q.z * q.z) + 1.0;
double t1 = +2.0 * (q.x * q.y + q.w * q.z);
double t2 = -2.0 * (q.x * q.z - q.w * q.y);
double t3 = +2.0 * (q.y * q.z + q.w * q.x);
double t4 = -2.0 * (q.x * q.x + q2sqr) + 1.0;
t2 = t2 > 1.0 ? 1.0 : t2;
t2 = t2 < -1.0 ? -1.0 : t2;
e.x = atan2(t3, t4);
e.y = asin(t2);
e.z = atan2(t1, t0);
return e;
}
geometry_msgs::Quaternion rpy_to_quaternion(geometry_msgs::Vector3 e) {
geometry_msgs::Quaternion q;
double t0 = cos(e.z * 0.5);
double t1 = sin(e.z * 0.5);
double t2 = cos(e.x * 0.5);
double t3 = sin(e.x * 0.5);
double t4 = cos(e.y * 0.5);
double t5 = sin(e.y * 0.5);
q.w = t2 * t4 * t0 + t3 * t5 * t1;
q.x = t3 * t4 * t0 - t2 * t5 * t1;
q.y = t2 * t5 * t0 + t3 * t4 * t1;
q.z = t2 * t4 * t1 - t3 * t5 * t0;
return q;
}For a simple waypoint system, we would provide some form of goal state (pose, velocity, etc.) for the robot to reach. This process is considered simple for a few reasons. Firstly, it does not consider the robots current state (for example, the robot may be traveling very quickly and will not be able to stop in time). Secondly, it does not allow for any additional guiding of the robot (for example, it assumes that the robot will get from A to B as quickly as possible, do so safely, not hit anything along the way, etc.). Thirdly, it assumes that the robot is capable of reaching the desired state (for example, it cannot turn quick enough, it can't travel to a certain height, etc.). Regardless, a simple waypoint system is usually the first step to something smarter.
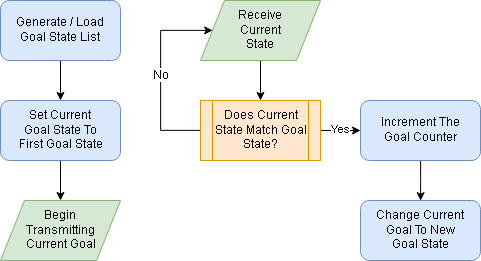
Continuing on, we will break down simple waypoint tracking in relation to navigating multirotor aircraft.
Firstly, it is assumed that the process of transmitting the current goal is being taken care of in a main() loop, or in a timer callback of some kind. Through this process, it is assumed that there is a "global" variable that is called to send out the current goal, and by changing this variable, the the next time the current goal is sent, it will automatically send out the changed version. This is in line with how the PX4 and Robin autopilots expect a "continuous stream" of command inputs before accepting the information. For a more in-depth example of sending a single waypoint, look towards the MAVROS Offboard Example or the mavros_guider sample package.
Before creating any sort of waypoint/goal state list, we must first decide on what we will be trying to control. For a multirotor UAV, it is probably desirable to control the entire pose (i.e. position and orientation), thus we will require a list of poses to use as our goals. For integration with ROS, this works out quite well, as the current goal that will be transmitted will most likely be of the type geometry_msgs/PoseStamped, and we can simply override the our output pose goal with a pose goal from a list of geometry_msgs/Pose goals.
Python
from geometry_msgs.msg import PoseStamped
from geometry_msgs.msg import Pose
global waypoint_list
global waypoint_counter
global output_goal
...
# Main
waypoint_list = []
waypoint_counter = 0
# In a loop
tmp_wp = Pose()
#tmp_wp = ... # Load/Generate waypoints somehow
waypoint_list.append(tmp_wp)
output_goal.pose = waypoint_list[waypoint_counter]
...
# In a function that checks the current state of the robot
# If current state matches goal state
waypoint_counter += 1
output_goal.pose = waypoint_list[waypoint_counter]C++
#import "geometry_msgs/PoseStamped"
#import "geometry_msgs/Pose"
#import <vector>
std::vector<geometry_msgs/Pose> waypoint_list;
uint waypoint_counter = 0;
geometry_msgs/PoseStamped output_goal;
...
# Main
# In a loop
geometry_msgs::Pose tmp_wp;
#tmp_wp = ... # Load/Generate waypoints somehow
waypoint_list.push_back(tmp_wp);
output_goal.pose = waypoint_list[waypoint_counter];
...
# In a function that checks the current state of the robot
# If current state matches goal state
waypoint_counter++;
output_goal.pose = waypoint_list[waypoint_counter];Now that we have a method for loading/generating sending goals, we just need a method to check when we have officially reached a goal. For position, the most common way to do this is through a radius-based technique. As we cannot be certain that a robot will be exactly at x=1.0 (as it may be at x=0.99999), we usually rely on calculating the distance the robot is away from the goal, and having some sort of threshold to say that "close enough is good enough".
For example, we can use the distance between the two positions, and Pythagoras's Theorem to calculate the radial distance, then compare that to some goal radius:
# The following are already known values: x_pos, y_pos, z_pos, x_goal, y_goal, z_goal
delta_x = x_goal - x_pos
delta_y = y_goal - y_pos
delta_z = z_goal - z_pos
r_dist = sqrt( delta_x*delta_x + delta_y*delta_y + delta_z*delta_z )
# If the radial distance is less than 5cm
if r_dist < 0.05
# The waypoint has been reached!
For orientation, there are a few ways that this can be handled. For a multirotor UAV, we are most likely only interested in the Yaw rotation. In this case, we can do a similar check to make sure the difference between the current yaw and the goal yaw is low (for example, less than 10°D).
To further improve the the waypoint algorithms, there are a few small things that can be done. Firstly, it may be a good idea to ensure your robot is controlled well enough to reach your successfully (if the robot is not very precise, you may need a much larger waypoint radius). Secondly, it may be a good idea to make sure the robot remains within the waypoint for a specific amount of time (take a timestamp when the robot enters the waypoint, reset it if it leaves, and count if as reached if enough time has passed without a reset).
It is often desirable to think about the environment in some sort of discrete grid as it allows us to say that at a very specific location, there is a specific thing that takes up a specific amount of space. While something similar can be achieved with a more free-form method, such as saying there is a circular object of a certain size at these coordinates, it can often be difficult to get decent estimates of these types of methods, which can lead to uncertainties of all different types.
For such reasons, having a discrete grid to work in, one that says there is nothing in this location, but there is something in this other location, allows us to be much more general with the type of solution we implement.
In the 2D plane, we can look at a grid that will approximate where we can and can't go. For most cases, the most realistic application of this is as a top-down view of the mapped area. Such a grid is usually referred to as an occupancy grid.
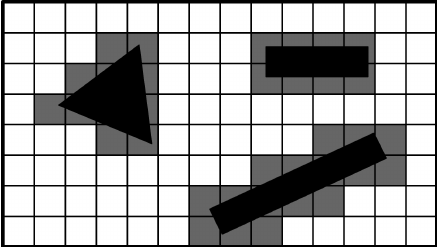
Within the mapped area, we may have certain obstacles that have been detected in some fashion (e.g. using a rangefinder), or are already known through some other means. In the example above, there are multiple blocks that have been placed in the mapped area, and then discretized in such a way that the shape is completely bounded by the grayed out sections of the map. In this case, this may tell the robot to avoid moving close to those regions, otherwise it may hit the objects.
We can use the data provided by an occupancy grid to perform algorithms such as A* (or anything else of the like) to conveniently navigate around the room in an optimal manner (assuming that optimal in the case of the robot is the shortest path).
One setback is that the occupancy grid data may not be formatted in a way that is easy to implement a navigation algorithm on (such as the data received by the ROS Occupancy Grid message). In this case, you may want to check out the image processing documentation on handling remapped arrays.
Furthermore, any implemented algorithms will expect starting and finish points to be in map coordinates, and will output the an goal steps in the same coordinates. Below is an example on converting between meters and map coordinates (and will get the center points of each grid location)
From World to Map
# Configure the map details
map_origin_x = -2.0
map_origin_y = -2.0
map_resolution = 0.1
# Known coordinates
x = -0.9 # Map location width
y = 1.0 # Map location height
# Calculate offset from map origin in meters, then convert to map coords
di = (x - map_origin_x) / map_resolution
dj = (y - map_origin_y) / map_resolution
# Round down or convert to integer
i = floor(di)
j = floor(dj)From Map to World
# Configure the map details
map_origin_x = -2.0
map_origin_y = -2.0
map_resolution = 0.1
# Known coordinates
i = 10 # Map location width
j = 30 # Map location height
# Calculate offset from (0,0) in meters (plus half a square to center coordinate)
dx = (i * map_resolution) + (map_resolution / 2)
dy = (j * map_resolution) + (map_resolution / 2)
# Final position in the world
x = map_origin_x + dx
y = map_origin_y + dyAs an additional idea, it may be good to inflate detected objects on the map in such a way that an additional buffer is in place, typically half this size of the robot. The reason for this is so that any pathplanning methods that are performed will then inherently take into consideration the size of the robot, such that the final navigation won't tell the robot to move too close to an obstacle, but rather as close as possible without breaking the buffer.