You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.
Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
Example 1:
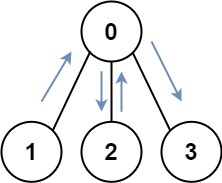
Input: graph = [[1,2,3],[0],[0],[0]] Output: 4 Explanation: One possible path is [1,0,2,0,3]
Example 2:
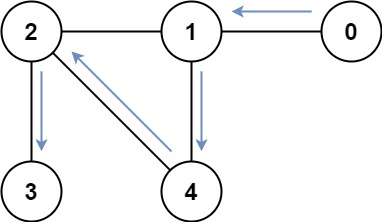
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]] Output: 4 Explanation: One possible path is [0,1,4,2,3]
Constraints:
n == graph.length1 <= n <= 120 <= graph[i].length < ngraph[i]does not containi.- If
graph[a]containsb, thengraph[b]containsa. - The input graph is always connected.
Related Topics:
Dynamic Programming, Bit Manipulation, Breadth-First Search, Graph, Bitmask
Intuitions:
- Shortest path -> BFS
Let (u, mask) be a state where we've visited nodes represented by mask and the last node visited is u.
For a neighbor node of u, we can transition from (u, mask) to (v, mask | (1 << v)) in one step.
We can BFS from initial states (i, 1 << i) (0 <= i < N) and count the steps needed to make mask the full graph.
// OJ: https://leetcode.com/problems/shortest-path-visiting-all-nodes/
// Author: github.com/lzl124631x
// Time: O(2^N * N)
// Space: O(2^N * N)
// Ref: https://leetcode.com/problems/shortest-path-visiting-all-nodes/discuss/135809/Fast-BFS-Solution-(46ms)-Clear-Detailed-Explanation-Included
class Solution {
int getKey(int i, int mask) {
return (i << 12) + mask;
}
public:
int shortestPathLength(vector<vector<int>>& G) {
int N = G.size(), step = 0, all = (1 << N) - 1;
queue<int> q;
unordered_set<int> seen;
for (int i = 0; i < N; ++i) {
int key = getKey(i, 1 << i);
q.push(key);
seen.insert(key);
}
while (q.size()) {
int cnt = q.size();
while (cnt--) {
int key = q.front(), u = key >> 12, visited = key & ((1 << 12) - 1);
q.pop();
if (visited == all) return step;
for (int v : G[u]) {
int next = getKey(v, visited | (1 << v));
if (seen.count(next)) continue;
seen.insert(next);
q.push(next);
}
}
++step;
}
return -1;
}
};// OJ: https://leetcode.com/problems/shortest-path-visiting-all-nodes
// Author: github.com/lzl124631x
// Time: O(2^N * N^2)
// Space: O(2^N * N)
class Solution {
int getKey(int i, int mask) {
return (i << 12) + mask;
}
public:
int shortestPathLength(vector<vector<int>>& G) {
int N = G.size(), ans = INT_MAX;
unordered_map<int, int> m;
function<int(int, int)> dfs = [&](int u, int visited) {
int key = getKey(u, visited);
if (m.count(key)) return m[key];
if (__builtin_popcount(visited) == N) return 0;
m[key] = INT_MAX - 1; // Upon visiting this state, we mark this state as visiting by setting its steps as `Infinity`, to prevent revisiting this state later which won't be optimal
for (int v : G[u]) {
if (visited >> v & 1) continue;
int a = dfs(v, visited); // we go to node `v` without marking `v` as visited so that we can revisit v later.
int b = dfs(v, visited | (1 << v)); // we go to node `v` and mark it as visited.
m[key] = min(m[key], 1 + min(a, b)); // we pick the minimum steps from the above two cases, plus 1 which is the step from `u` to `v`.
}
return m[key];
};
for (int i = 0; i < N; ++i) {
ans = min(ans, dfs(i, 1 << i));
}
return ans;
}
};