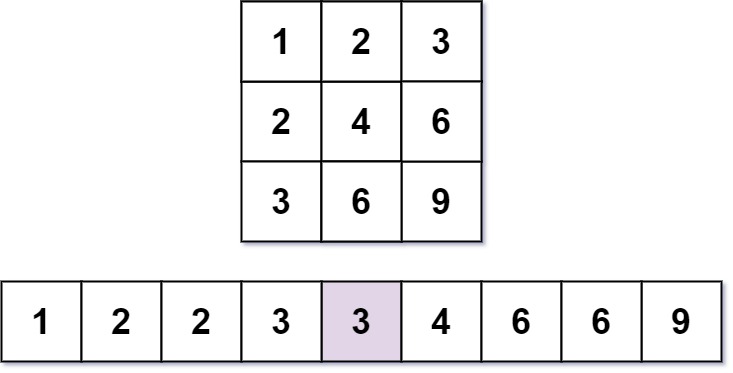
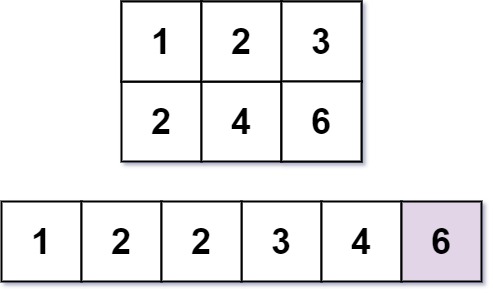
Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).
Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.
Example 1:
Input: m = 3, n = 3, k = 5 Output: 3 Explanation: The 5th smallest number is 3.
Example 2:
Input: m = 2, n = 3, k = 6 Output: 6 Explanation: The 6th smallest number is 6.
Constraints:
1 <= m, n <= 3 * 1041 <= k <= m * n
Companies:
Rubrik
Related Topics:
Binary Search
Similar Questions:
- Kth Smallest Element in a Sorted Matrix (Medium)
- Find K-th Smallest Pair Distance (Hard)
- K-th Smallest Prime Fraction (Hard)
The range of the answer is [1, m * n]. We can use binary answer to find it.
Let L = 1, R = m * n, M = (L + R) / 2.
Define cnt(M) as the count of numbers less than or equal to M.
For the answer ans, the corresponding cnt(ans) could be exactly k (when there is only one ans in the table) or greater than k (when there are multiple ans in the table).
The goal is to find the first element M whose cnt(M) is greater than or equal to k.
So let the left part of the array be those elements whose cnt < k, and the right part be cnt >= k.
In the end, L will point to the first element whose cnt >= k and it is the answer.
// OJ: https://leetcode.com/problems/kth-smallest-number-in-multiplication-table/
// Author: github.com/lzl124631x
// Time: O(Mlog(MN))
// Space: O(1)
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int L = 1, R = m * n;
auto valid = [&](int num) {
int cnt = 0, last = min(m, num); // count the numbers that are less than or equal to `num`
for (int i = 1; i <= last; ++i) cnt += min(num / i, n);
return cnt >= k;
};
while (L <= R) {
int M = L + (R - L) / 2;
if (valid(M)) R = M - 1;
else L = M + 1;
}
return L;
}
};Or use L < R template
// OJ: https://leetcode.com/problems/kth-smallest-number-in-multiplication-table/
// Author: github.com/lzl124631x
// Time: O(Mlog(MN))
// Space: O(1)
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int L = 1, R = m * n;
auto valid = [&](int num) {
int cnt = 0, last = min(m, num);// count the numbers that are less than or equal to `num`
for (int i = 1; i <= last; ++i) cnt += min(num / i, n);
return cnt >= k;
};
while (L < R) {
int M = L + (R - L) / 2;
if (valid(M)) R = M;
else L = M + 1;
}
return L;
}
};