666

666. Path Sum IV (Medium)

If the depth of a tree is smaller than 5, then this tree can be represented by an array of three-digit integers. For each integer in this array:

• The hundreds digit represents the depth d of this node where 1 <= d <= 4.
• The tens digit represents the position p of this node in the level it belongs to where 1 <= p <= 8. The position is the same as that in a full binary tree.
• The units digit represents the value v of this node where 0 <= v <= 9.

Given an array of ascending three-digit integers nums representing a binary tree with a depth smaller than 5, return the sum of all paths from the root towards the leaves.

It is guaranteed that the given array represents a valid connected binary tree.

 

Example 1:

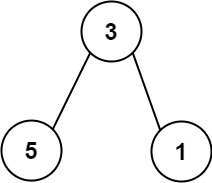
Input: nums = [113,215,221]
Output: 12
Explanation: The tree that the list represents is shown.
The path sum is (3 + 5) + (3 + 1) = 12.

Example 2:

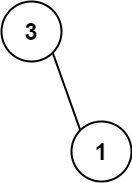
Input: nums = [113,221]
Output: 4
Explanation: The tree that the list represents is shown. 
The path sum is (3 + 1) = 4.

 

Constraints:

• 1 <= nums.length <= 15
• 110 <= nums[i] <= 489
• nums represents a valid binary tree with depth less than 5.

Companies:
Facebook

Related Topics:
Array, Tree, Depth-First Search, Binary Tree

Similar Questions:

• Path Sum (Easy)
• Path Sum II (Medium)
• Binary Tree Maximum Path Sum (Hard)
• Path Sum III (Medium)

Solution 1.

// OJ: https://leetcode.com/problems/path-sum-iv/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int pathSum(vector<int>& nums) {
        unordered_map<int, int> m;
        for (int n : nums) {
            m[n / 10] = n % 10;
        }
        int sum = 0;
        for (int n : nums) {
            int d = n / 100, p = n / 10 % 10, v = m[d * 10 + p];
            int left = (d + 1) * 10 + p * 2 - 1, right = left + 1;
            if (m.count(left)) m[left] += v;
            if (m.count(right)) m[right] += v;
            if (m.count(left) == 0 && m.count(right) == 0) sum += v;
        }
        return sum;
    }
};

Solution 2.

// OJ: https://leetcode.com/problems/path-sum-iv/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
    int vals[33] = {[0 ... 32] = -1}, ans = 0;
    void dfs(int i, int sum) {
        if (vals[i] == -1) return;
        sum += vals[i];
        int left = 2 * i, right = 2 * i + 1;
        if (vals[left] == -1 && vals[right] == -1) {
            ans += sum;
            return;
        }
        dfs(left, sum);
        dfs(right, sum);
    }
public:
    int pathSum(vector<int>& A) {
        for (int n : A) {
            int lv = n / 100, index = n % 100 / 10, val = n % 10, i = (1 << (lv - 1)) - 1 + index;
            vals[i] = val;
        }
        dfs(1, 0);
        return ans;
    }
};