Symbolic regression solver, based on genetic programming methodology.
- Description
1.1 Crossover
1.2 Mutation
1.3 Optimization of coefficients
1.4 Reducing complexity of syntax trees - Demo
2.1 f(x,y,z) - ? - Quick start
3.1 Just download jar
3.2 Try it with Maven
3.3 Hello world
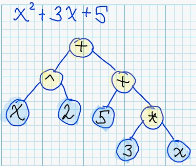
Each mathematical expression can be represented in form of syntax tree:
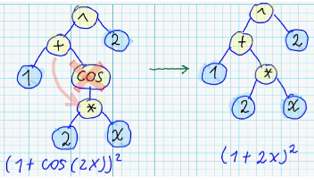
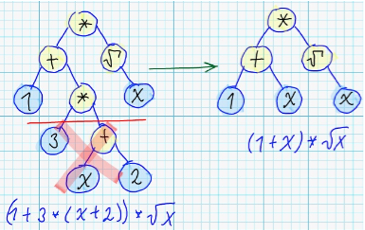
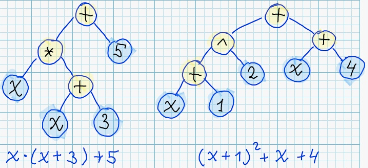
Actually, it worth to keep in mind, that there exists infinite number of different syntax trees, which corresponds to semantically equivalent expressions. For example:
In practice, on of the most generic problems - is reconstruction of original function, having the information about its values in some specific points.
It is possible to apply genetic algorithm - for solving of given problem:
-
In terms of Genetic Algorithm - each syntax tree can be treated as a "chromosome" (an entity, which can "mutate" and change by "crossover" with other "chromosome")
-
It is needed to define fitness function: the function, which will calculate, how good each formula (which was encoded by syntax tree) - can represent existing data (e.g.: using mean squared error value).
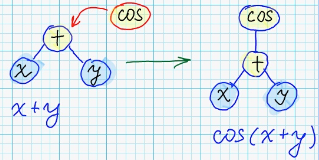
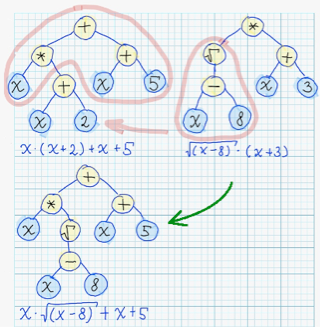
During "crossover" - syntax tree is modified by substituion of its subtree, with some subtree from other syntax tree.
Following image explains implementation of "crossover" operation over syntax trees:
Currently implemented following "mutation" operations:
-
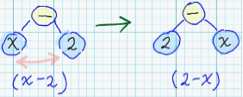
Substituion of some node of syntax tree - with node, which corresponds to different arithmetical operation:
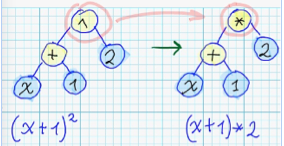
-
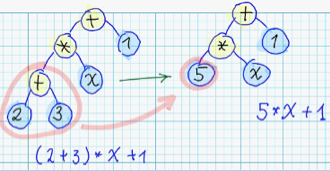
Substituion of some subtree with randomly generated subtree:
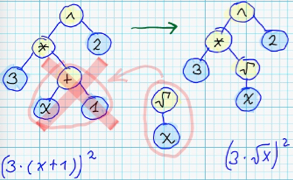
Actually, some syntax tree might represent correct structure of searchable function, but due to some non-optimal values of coefficients - given syntax tree can be considered as non-optimal by fitness function.
For example, following image displays target values of searchable function (red crosses) - and two functions-candidates (green and blue):
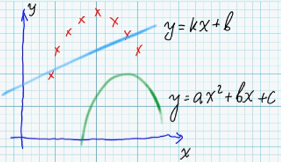
Blue line has smaller value of mean squared error, but, actually - green parabola - would be a better candidate for the final solution.
By this reason, current implementation of Symbolic Regression Solver - uses second pass of Genetic Algorithm - for optimizing of coefficients of each syntax tree. On the picture below - represented the way, how coefficients of each syntax tree - could be transformed to "chromosome":
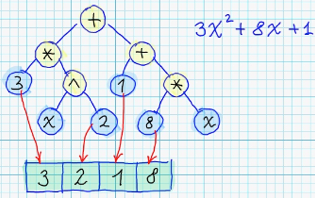
Lets try to reconstruct original function, by following target values:
| x | y | z | f(x,y,z) |
|---|---|---|---|
| 26 | 35 | 1 | 830 |
| 8 | 24 | -11 | 130 |
| 20 | 1 | 10 | 477 |
| 33 | 11 | 2 | 1217 |
| 37 | 16 | 7 | 1524 |
Lets launch console application for "evolving" of f(x,y,z):
-
Download http://github.com/lagodiuk/genetic-programming/tree/master/bin/symbolic_regression_1.0.jar
-
Create file xyz.txt with following content:
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS # set which functions to use: ADD MUL SUB # looking for: f(x, y, z) — ? # define training set: f(26, 35, 1) = 830 f(8, 24, -11) = 130 f(20, 1, 10) = 477 f(33, 11, 2) = 1217 f(37, 16, 7) = 1524
(this file can be downloaded from: https://github.com/lagodiuk/genetic-programming/blob/master/bin/xyz.txt)
-
Launch:
java -jar symbolic_regression_1.0.jar xyz.txt- and observe output for each iteration (output will be in format: iteration numbre, value of mean squared error, and evolved formula).
Below presented picture, which shows dynamics of changes of mean squared error, according to the best "evolved" syntax trees (the axis "x" - represents number of iteration):
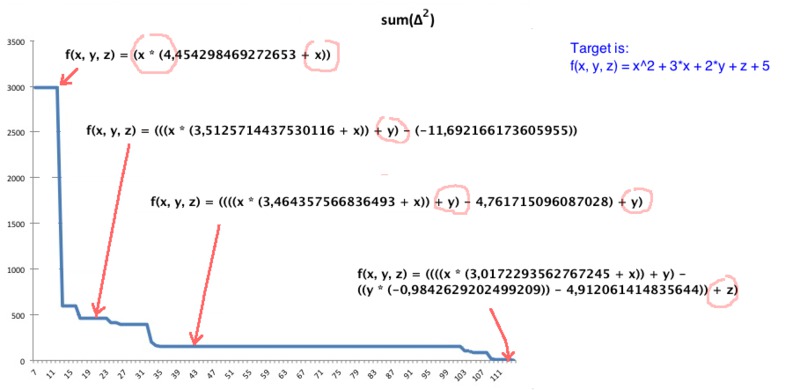
The most simple way is download http://github.com/lagodiuk/genetic-programming/tree/master/bin/symbolic_regression_1.0.jar and add it to your classpath.
This project depends on Generic Genetic Algorithm project (as a maven dependency).
- git clone https://github.com/lagodiuk/genetic-algorithm.git
- git clone https://github.com/lagodiuk/genetic-programming.git
- mvn -f genetic-algorithm/pom.xml install
- mvn -f genetic-programming/pom.xml install
Now you can add following maven dependencies to your project:
<dependency>
<groupId>com.lagodiuk</groupId>
<artifactId>ga</artifactId>
<version>1.0.1</version>
</dependency>
<dependency>
<groupId>com.lagodiuk</groupId>
<artifactId>gp</artifactId>
<version>1.0</version>
</dependency>import java.util.LinkedList;
import java.util.List;
import com.lagodiuk.gp.symbolic.SymbolicRegressionEngine;
import com.lagodiuk.gp.symbolic.SymbolicRegressionIterationListener;
import com.lagodiuk.gp.symbolic.TabulatedFunctionFitness;
import com.lagodiuk.gp.symbolic.Target;
import com.lagodiuk.gp.symbolic.interpreter.Expression;
import com.lagodiuk.gp.symbolic.interpreter.Functions;
/**
* f(x) - ? <br/>
*
* f(0) = 0 <br/>
* f(1) = 11 <br/>
* f(2) = 24 <br/>
* f(3) = 39 <br/>
* f(4) = 56 <br/>
* f(5) = 75 <br/>
* f(6) = 96 <br/>
*
* (target function is f(x) = x^2 + 10*x)
*/
public class HelloSymbolicRegression {
public static void main(String[] args) {
// define training set
TabulatedFunctionFitness fitness =
new TabulatedFunctionFitness(
new Target().when("x", 0).targetIs(0),
new Target().when("x", 1).targetIs(11),
new Target().when("x", 2).targetIs(24),
new Target().when("x", 3).targetIs(39),
new Target().when("x", 4).targetIs(56),
new Target().when("x", 5).targetIs(75),
new Target().when("x", 6).targetIs(96));
SymbolicRegressionEngine engine =
new SymbolicRegressionEngine(
fitness,
// define variables
list("x"),
// define base functions
list(Functions.ADD, Functions.SUB, Functions.MUL, Functions.VARIABLE, Functions.CONSTANT));
addListener(engine);
// 200 iterations
engine.evolve(200);
}
/**
* Track each iteration
*/
private static void addListener(SymbolicRegressionEngine engine) {
engine.addIterationListener(new SymbolicRegressionIterationListener() {
@Override
public void update(SymbolicRegressionEngine engine) {
Expression bestSyntaxTree = engine.getBestSyntaxTree();
double currFitValue = engine.fitness(bestSyntaxTree);
// log to console
System.out.println(
String.format("iter = %s \t fit = %s \t func = %s",
engine.getIteration(), currFitValue, bestSyntaxTree.print()));
// halt condition
if (currFitValue < 5) {
engine.terminate();
}
}
});
}
private static <T> List<T> list(T... items) {
List<T> list = new LinkedList<T>();
for (T item : items) {
list.add(item);
}
return list;
}
}Some additional information can be found in the following article (in Russian language).