README_EN.md

comments	difficulty	edit_url	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/0700-0799/0743.Network%20Delay%20Time/README_EN.md	Depth-First Search Breadth-First Search Graph Shortest Path Heap (Priority Queue)

743. Network Delay Time

中文文档

Description

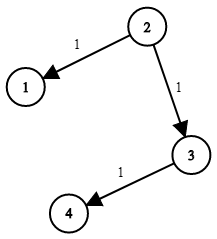
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.

We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.

 

Example 1:

Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

Example 2:

Input: times = [[1,2,1]], n = 2, k = 1
Output: 1

Example 3:

Input: times = [[1,2,1]], n = 2, k = 2
Output: -1

 

Constraints:

• 1 <= k <= n <= 100
• 1 <= times.length <= 6000
• times[i].length == 3
• 1 <= ui, vi <= n
• ui != vi
• 0 <= wi <= 100
• All the pairs (ui, vi) are unique. (i.e., no multiple edges.)

Solutions

Solution 1: Naive Dijkstra Algorithm

We define $\textit{g}[u][v]$ to represent the edge weight from node $u$ to node $v$. If there is no edge between node $u$ and node $v$, then $\textit{g}[u][v] = +\infty$.

We maintain an array $\textit{dist}$, where $\textit{dist}[i]$ represents the shortest path length from node $k$ to node $i$. Initially, we set all $\textit{dist}[i]$ to $+\infty$, except for $\textit{dist}[k - 1] = 0$. We define an array $\textit{vis}$, where $\textit{vis}[i]$ indicates whether node $i$ has been visited. Initially, we set all $\textit{vis}[i]$ to $\text{false}$.

Each time, we find the unvisited node $t$ with the smallest distance, and then perform relaxation operations centered on node $t$. For each node $j$, if $\textit{dist}[j] > \textit{dist}[t] + \textit{g}[t][j]$, we update $\textit{dist}[j] = \textit{dist}[t] + \textit{g}[t][j]$.

Finally, we return the maximum value in $\textit{dist}$ as the answer. If the answer is $+\infty$, it means there are unreachable nodes, and we return $-1$.

The time complexity is $O(n^2 + m)$, and the space complexity is $O(n^2)$. Here, $n$ and $m$ are the number of nodes and edges, respectively.

Python3

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        g = [[inf] * n for _ in range(n)]
        for u, v, w in times:
            g[u - 1][v - 1] = w
        dist = [inf] * n
        dist[k - 1] = 0
        vis = [False] * n
        for _ in range(n):
            t = -1
            for j in range(n):
                if not vis[j] and (t == -1 or dist[t] > dist[j]):
                    t = j
            vis[t] = True
            for j in range(n):
                dist[j] = min(dist[j], dist[t] + g[t][j])
        ans = max(dist)
        return -1 if ans == inf else ans

Java

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        int[][] g = new int[n][n];
        int[] dist = new int[n];
        final int inf = 1 << 29;
        Arrays.fill(dist, inf);
        for (var e : g) {
            Arrays.fill(e, inf);
        }
        for (var e : times) {
            g[e[0] - 1][e[1] - 1] = e[2];
        }
        dist[k - 1] = 0;
        boolean[] vis = new boolean[n];
        for (int i = 0; i < n; ++i) {
            int t = -1;
            for (int j = 0; j < n; ++j) {
                if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 0; j < n; ++j) {
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = 0;
        for (int x : dist) {
            ans = Math.max(ans, x);
        }
        return ans == inf ? -1 : ans;
    }
}

C++

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        const int inf = 1 << 29;
        vector<vector<int>> g(n, vector<int>(n, inf));
        for (const auto& e : times) {
            g[e[0] - 1][e[1] - 1] = e[2];
        }
        vector<int> dist(n, inf);
        dist[k - 1] = 0;
        vector<bool> vis(n);
        for (int i = 0; i < n; ++i) {
            int t = -1;
            for (int j = 0; j < n; ++j) {
                if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 0; j < n; ++j) {
                dist[j] = min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = ranges::max(dist);
        return ans == inf ? -1 : ans;
    }
};

Go

func networkDelayTime(times [][]int, n int, k int) int {
	const inf = 1 << 29
	g := make([][]int, n)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			g[i][j] = inf
		}
	}
	for _, e := range times {
		g[e[0]-1][e[1]-1] = e[2]
	}

	dist := make([]int, n)
	for i := range dist {
		dist[i] = inf
	}
	dist[k-1] = 0

	vis := make([]bool, n)
	for i := 0; i < n; i++ {
		t := -1
		for j := 0; j < n; j++ {
			if !vis[j] && (t == -1 || dist[t] > dist[j]) {
				t = j
			}
		}
		vis[t] = true
		for j := 0; j < n; j++ {
			dist[j] = min(dist[j], dist[t]+g[t][j])
		}
	}

	if ans := slices.Max(dist); ans != inf {
		return ans
	}
	return -1
}

TypeScript

function networkDelayTime(times: number[][], n: number, k: number): number {
    const g: number[][] = Array.from({ length: n }, () => Array(n).fill(Infinity));
    for (const [u, v, w] of times) {
        g[u - 1][v - 1] = w;
    }
    const dist: number[] = Array(n).fill(Infinity);
    dist[k - 1] = 0;
    const vis: boolean[] = Array(n).fill(false);
    for (let i = 0; i < n; ++i) {
        let t = -1;
        for (let j = 0; j < n; ++j) {
            if (!vis[j] && (t === -1 || dist[j] < dist[t])) {
                t = j;
            }
        }
        vis[t] = true;
        for (let j = 0; j < n; ++j) {
            dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
        }
    }
    const ans = Math.max(...dist);
    return ans === Infinity ? -1 : ans;
}

Solution 2: Heap-Optimized Dijkstra Algorithm

We can use a priority queue (heap) to optimize the naive Dijkstra algorithm.

We define $\textit{g}[u]$ to represent all adjacent edges of node $u$, and $\textit{dist}[u]$ to represent the shortest path length from node $k$ to node $u$. Initially, we set all $\textit{dist}[u]$ to $+\infty$, except for $\textit{dist}[k - 1] = 0$.

We define a priority queue $\textit{pq}$, where each element is $(\textit{d}, u)$, representing the distance $\textit{d}$ from node $u$ to node $k$. Each time, we take out the node $(\textit{d}, u)$ with the smallest distance from $\textit{pq}$. If $\textit{d} > $\textit{dist}[u]$, we skip this node. Otherwise, we traverse all adjacent edges of node $u$. For each adjacent edge $(v, w)$, if $\textit{dist}[v] > \textit{dist}[u] + w$, we update $\textit{dist}[v] = \textit{dist}[u] + w$ and add $(\textit{dist}[v], v)$ to $\textit{pq}$.

Finally, we return the maximum value in $\textit{dist}$ as the answer. If the answer is $+\infty$, it means there are unreachable nodes, and we return $-1$.

The time complexity is $O(m \times \log m + n)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ are the number of nodes and edges, respectively.

Python3

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        g = [[] for _ in range(n)]
        for u, v, w in times:
            g[u - 1].append((v - 1, w))
        dist = [inf] * n
        dist[k - 1] = 0
        pq = [(0, k - 1)]
        while pq:
            d, u = heappop(pq)
            if d > dist[u]:
                continue
            for v, w in g[u]:
                if (nd := d + w) < dist[v]:
                    dist[v] = nd
                    heappush(pq, (nd, v))
        ans = max(dist)
        return -1 if ans == inf else ans

Java

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        final int inf = 1 << 29;
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : times) {
            g[e[0] - 1].add(new int[] {e[1] - 1, e[2]});
        }
        int[] dist = new int[n];
        Arrays.fill(dist, inf);
        dist[k - 1] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        pq.offer(new int[] {0, k - 1});
        while (!pq.isEmpty()) {
            var p = pq.poll();
            int d = p[0], u = p[1];
            if (d > dist[u]) {
                continue;
            }
            for (var e : g[u]) {
                int v = e[0], w = e[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    pq.offer(new int[] {dist[v], v});
                }
            }
        }
        int ans = Arrays.stream(dist).max().getAsInt();
        return ans == inf ? -1 : ans;
    }
}

C++

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        const int inf = 1 << 29;
        using pii = pair<int, int>;
        vector<vector<pii>> g(n);
        for (auto& edge : times) {
            g[edge[0] - 1].emplace_back(edge[1] - 1, edge[2]);
        }

        vector<int> dist(n, inf);
        dist[k - 1] = 0;
        priority_queue<pii, vector<pii>, greater<>> pq;
        pq.emplace(0, k - 1);

        while (!pq.empty()) {
            auto [d, u] = pq.top();
            pq.pop();
            if (d > dist[u]) {
                continue;
            }
            for (auto& [v, w] : g[u]) {
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    pq.emplace(dist[v], v);
                }
            }
        }

        int ans = ranges::max(dist);
        return ans == inf ? -1 : ans;
    }
};

Go

func networkDelayTime(times [][]int, n int, k int) int {
	g := make([][][2]int, n)
	for _, e := range times {
		u, v, w := e[0]-1, e[1]-1, e[2]
		g[u] = append(g[u], [2]int{v, w})
	}
	dist := make([]int, n)
	const inf int = 1 << 29
	for i := range dist {
		dist[i] = inf
	}
	dist[k-1] = 0
	pq := hp{{0, k - 1}}
	for len(pq) > 0 {
		p := heap.Pop(&pq).(pair)
		d, u := p.x, p.i
		if d > dist[u] {
			continue
		}
		for _, e := range g[u] {
			v, w := e[0], e[1]
			if nd := d + w; nd < dist[v] {
				dist[v] = nd
				heap.Push(&pq, pair{nd, v})
			}
		}
	}
	if ans := slices.Max(dist); ans < inf {
		return ans
	}
	return -1

}

type pair struct{ x, i int }
type hp []pair

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].x < h[j].x }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(x any)        { *h = append(*h, x.(pair)) }
func (h *hp) Pop() (x any)      { a := *h; x = a[len(a)-1]; *h = a[:len(a)-1]; return }

TypeScript

function networkDelayTime(times: number[][], n: number, k: number): number {
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [u, v, w] of times) {
        g[u - 1].push([v - 1, w]);
    }
    const dist: number[] = Array(n).fill(Infinity);
    dist[k - 1] = 0;
    const pq = new MinPriorityQueue({ priority: v => v[0] });
    pq.enqueue([0, k - 1]);
    while (!pq.isEmpty()) {
        const [d, u] = pq.dequeue().element;
        if (d > dist[u]) {
            continue;
        }
        for (const [v, w] of g[u]) {
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                pq.enqueue([dist[v], v]);
            }
        }
    }
    const ans = Math.max(...dist);
    return ans === Infinity ? -1 : ans;
}