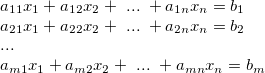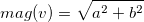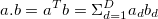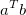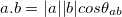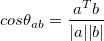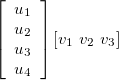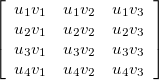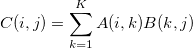One of the most basic motivations towards making computers was solving a system linear equations given by
where 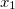
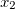
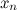
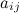
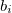
A system 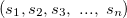
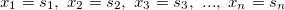
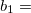
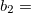
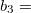

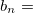
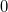
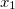
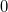
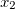
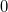
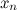
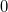
A vector is a numeric measurement with directions. In two dimensions, a vector 
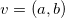
There are two ways to go about this:
-
This is the summation of element wise multiplication of the two vectors. The notation
denotes that the vectors are column vectors and the result of the equation above would be a 1x1 vector which is a scalar quantity.
This notation is not very convenient for vector multiplication unless a the angle on the right hand side is known to us. Although, it is a much more common practice to use this equation for finding out the angle between two vectors using
The outer product of two vectors results in a matrix and is given by the equation:
If there are two column vectors u1 and v1 that are given by 

Matrices are two dimensional set of numbers. These are very efficient data types for quick computations.
The product of two matrices A and B in given by the formulae