diff --git a/README.md b/README.md
index b34946a..10ef2dd 100644
--- a/README.md
+++ b/README.md
@@ -1,12 +1,18 @@
# RareSkills Book of Zero Knowledge (ZK Book)
+En ESPAÑOL:
-The content is not stored in the main branch, please see the prod branch. If you see a typo or error, please feel free to submit a pull request.
+El contenido de este repositorio RareSkills_ZK-book/spanish-es (forked from RareSkills/zk-book) es una traduccion al idioma Español realizada por ARCADIO Garcia en el contexto de su contribución a la traduccion del libro ZK Book propiedad de RareSkills y que en ultima instancia será el que autorice su publicación.
+
+Nota IMPORTANTE: el propietario del contenido del libro ZK Book es RareSkills, por lo tanto tiene el copyright de esta contribución de la traduccion del libro al idioma Español.
+
+In ENGLISH:
+
+The content of this repository RareSkills_ZK-book/spanish-es (forked from RareSkills/zk-book) is a translation into Spanish made by ARCADIO Garcia in the context of his contribution to the translation of the book ZK Book owned by RareSkills and which will ultimately authorize its publication.
+
+IMPORTANT Note: the owner of the content of the book ZK Book is RareSkills, therefore it has the copyright of this contribution of the translation of the book into Spanish.
## Copyright and Disclaimer
Copyright Notice © RareSkills LLC 2024
All Rights Reserved.
All material learning material here (“content”) is protected by copyright under U.S. Copyright laws and is the property of RareSkills LLC or the party credited as the provider of the content. You may not copy, reproduce, distribute, publish, display, perform, modify, create derivative works, transmit, or in any way exploit any such content, nor may you distribute any part of this content over any network, including a local area network, sell or offer it for sale, or use such content to construct any kind of database. You may not alter or remove any copyright or other notice from copies of the content on the RareSkills website. Copying or storing any content except as provided above is expressly prohibited without prior written permission of the RareSkills or the copyright holder identified in the individual content’s copyright notice. For permission to use the content on the RareSkills' website, please contact contact - at - rareskills - io
-
-### Disclaimer
-The content contained in RareSkills’s website is provided only for educational and informational purposes or as required by U.S. law. RareSkills attempts to ensure that content is accurate and obtained from reliable sources, but does not represent it to be error-free. RareSkills does not warrant that any functions on its website will be uninterrupted, that defects will be corrected, or that the website will be free from viruses or other harmful components. Any links to third party information on the RareSkills’s website are provided as a courtesy and do not constitute an endorsement of those materials or the third party providing them.
diff --git a/content/set-theory.md b/content/set-theory.md
deleted file mode 100644
index 8b13789..0000000
--- a/content/set-theory.md
+++ /dev/null
@@ -1 +0,0 @@
-
diff --git a/spanish-es/abstract-algebra_es.md b/spanish-es/abstract-algebra_es.md
new file mode 100644
index 0000000..9f90679
--- /dev/null
+++ b/spanish-es/abstract-algebra_es.md
@@ -0,0 +1,203 @@
+# Álgebra Abstracta
+
+El álgebra abstracta es el estudio de los conjuntos que tienen uno o más operadores sobre ese conjunto. Para nuestros propósitos, sólo nos interesan los operadores binarios.
+
+Si tenemos conjuntos y un operador binario sobre ese conjunto, podemos categorizar esos conjuntos basándonos en cómo se comporta el operador binario, y qué elementos se permite (o se espera) que estén en el conjunto.
+
+Los matemáticos tienen una palabra para cada tipo posible de comportamiento del operador binario sobre el conjunto. Como programadores aplicados, nos preocupamos por el Grupo (de la Teoría de Grupos) en particular, pero vamos a ir avanzando de forma incremental. El grupo es sólo un tipo de animal en este gran zoo. Así que en lugar de estudiar el grupo de forma aislada, vamos a estudiar el grupo en su contexto más amplio de estructuras algebraicas relacionadas (es decir, conjuntos con un operador binario).
+
+El álgebra abstracta es un campo enorme, pero nuestro objetivo aquí es entender claramente lo que es un *Grupo* porque eso se usa en todas partes en Zero Knowledge Proofs. Podríamos dar una definición ahora mismo:
+
+*Un Grupo es un conjunto con un operador binario que es cerrado, asociativo, tiene un elemento identidad, y donde cada elemento tiene un inverso.*
+
+Pero eso no sería muy ilustrativo. Es más útil entender los grupos en su relación con el campo más amplio del Álgebra Abstracta.
+
+## Magma
+
+Un Magma es un conjunto con un operador binario cerrado. Eso es todo.
+
+Un Magma es definitivamente algo que entiendes intuitivamente como programador. Ahora tienes una palabra para definirlo.
+
+Como ejemplo, consideremos que nuestro conjunto sean todos los enteros positivos y que nuestro operador binario sea $x^y$. Tenga en cuenta que no permitimos números negativos porque si $y$ es negativo, obtenemos una fracción.
+
+Evidentemente, la salida estará en el espacio de los números enteros. Nuestra función es un subconjunto del producto cartesiano $(\mathbb{Z}\times\mathbb{Z})\times\mathbb{Z}$.
+
+Curiosamente, este ejemplo no es conmutativo ni asociativo. Puedes convencerte de ello eligiendo valores para a, b, y c en el código python de abajo.
+
+```python
+assert a ** (b ** c) != (a ** b) ** c
+assert a ** b != b ** a
+```
+
+Pero no nos importa. Un Magma es uno de los tipos menos restrictivos de *estructuras algebraicas*. Lo único que importa es que el operador binario sea cerrado. Todo lo demás es válido.
+
+Una estructura algebraica es un conjunto con una colección de operaciones sobre ese conjunto. Para nuestros propósitos, la única operación que nos importa es un operador binario.
+
+## Semigrupo
+
+Un Semigrupo es un Magma donde el operador binario debe ser asociativo.
+
+Todos los Semigrupos son Magmas, pero no todos los Magmas son Semigrupos.
+
+En otras palabras, un Semigrupo es un conjunto con un operador binario que es cerrado y asociativo.
+
+Sea nuestro conjunto (infinito) el conjunto de todas las posibles cadenas no vacías del alfabeto tradicional a, b, c, ..., x, y, z. Por ejemplo, “az”, “programador”, “cero”, “asdfghjk”, “foo” y “bar” están todas en este conjunto.
+
+Sea nuestro operador binario la concatenación de cadenas. Esto es cerrado, porque produce otra cadena en el conjunto.
+
+Observa que si conmutamos “foo” y “bar”, la cadena de salida no será la misma, es decir, “foobar” y “barfoo”. Sin embargo, eso no importa. Tanto “foobar” como “barfoo” son miembros del conjunto, por lo que el operador binario “concatenar” es cerrado. Como tenemos un conjunto con un operador binario cerrado y asociativo, el conjunto de todas las cadenas bajo concatenación es un Semigrupo.
+
+**Ejercicio:** Comprueba por ti mismo que concatenar “foo”, “bar”, “baz” en ese orden es asociativo. Recuerda, asociativo significa $(A \square B) \square C = A \square (B \square C)$, donde $\square$ es el operador binario del Semigrupo.
+
+**Ejercicio:** Pon un ejemplo de un Magma y un Semigrupo. El Magma no debe ser un Semigrupo. No utilices los ejemplos anteriores. Esto significa que debes pensar en un operador binario que sea cerrado pero no asociativo.
+
+## Monoide
+
+Un Monoide es un Semigrupo con un elemento identidad.
+
+Awww sí, este es el mismo Monoide de «Una mónada es un monoide en la categoría de endofunctores».
+
+
+
+Si miramos la [documentación del monoide](https://typelevel.org/cats/typeclasses/monoid.html) en la librería Cats para Scala, vemos estas definiciones explícitamente:
+
+```scala
+trait Semigroup[A] {
+ def combine(x: A, y: A): A
+}
+
+trait Monoid[A] extends Semigroup[A] {
+ def empty: A
+}
+```
+
+La librería Cats simplemente se refiere a la «identidad» como `empty` y al operador binario como `combine`. El hecho de que Monoid extends Semigroup muestra que un Monoid es un Semigrupo con el requisito de que tiene un "vacío" (identidad).
+
+El fragmento anterior no lo muestra, pero se requiere que combine sea asociativo.
+
+Un semigrupo sólo tiene un operador binario sin restricciones, excepto que la salida sea del mismo tipo (`A`) que las entradas (`x` e `y`).
+
+Por ejemplo, la suma de números enteros positivos sin cero es un semigrupo, pero si se incluye el cero, se convierte en un monoide.
+
+Un *elemento identidad* significa que si haces un operador binario con el elemento identidad y otro elemento $a$ , obtienes $a$ . En el ejemplo de la suma 8 + 0 = 8, donde 0 es el elemento identidad. Si nuestro operador binario fuera la multiplicación, entonces el elemento identidad sería 1, ya que al multiplicar por 1 obtenemos el mismo número.
+
+Si nuestro conjunto fuera el conjunto de todas las matrices de 2x2, el elemento identidad sería la matriz identidad
+
+$$
+\begin{bmatrix}
+1&0\\
+0&1\\
+\end{bmatrix}
+$$
+
+### Conjuntos de conjuntos sobre la unión y la intersección
+
+Algo que extrañamente estuvo ausente de nuestra discusión anterior sobre conjuntos fue la discusión sobre la unión y la intersección de conjuntos. Se trata de operadores binarios, y ahora es un buen momento para introducirlos.
+
+Si tomamos la unión de dos conjuntos $\set{1,2,3,4}$ y $\set{3,4,5,6}$, se obtiene $\set{1,2,3,4,5,6}$. Si se toma la intersección de $\set{1,2,3,4}$ y $\set{3,4,5,6}$ se obtiene $\set{3, 4}$ .
+
+Debe quedar claro que ambos operadores son asociativos.
+
+Si definimos nuestro dominio como el conjunto de todos los conjuntos finitos de números enteros, entonces los operadores binarios unión e intersección son cerrados porque su resultado es un conjunto de números enteros.
+
+La unión de conjuntos tiene un elemento de identidad en este dominio: el conjunto vacío $\set{}$. Si se toma la unión de un conjunto con el conjunto vacío, se obtiene el conjunto original, es decir, $A \cup \set{} = A$.
+
+Por lo tanto, el conjunto de todos los conjuntos *finitos* de números enteros sobre la unión es un Monoide.
+
+Sin embargo, en el conjunto de todos los posibles conjuntos finitos de enteros bajo intersección ($\cap$), es un Semigrupo -- ningún conjunto finito funcionará como la identidad. Pero si ampliamos este conjunto para incluir ℤ sí mismo -- es decir, nuestro conjunto es $\{\text{todos los conjuntos finitos de enteros}\}\cup\mathbb{\{Z\}}$ bajo la intersección, entonces eso es ser un Monoide, como $\mathbb{Z}$ es el elemento identidad.
+
+Si se siente como que hemos «hackeado» el elemento de identidad, es que lo hemos hecho.
+
+Veremos más adelante que las curvas elípticas utilizan un truco como este e incluyen un punto especial llamado «punto en el infinito» para mantener la coherencia con las leyes algebraicas. La cuestión es que tenemos que tener muy claro cuál es nuestro elemento de identidad si decimos que un conjunto es un Monoide sobre algún operador binario.
+
+Como otro ejemplo, podríamos decir que nuestro conjunto son todos los enteros positivos bajo adición, con el elemento adicional $\text{mug}$. Definimos $\text{mug} + x = x$ y $x + \text{mug} = x$. Como arquitectos de los sistemas, podemos hacer que nuestro conjunto consista en lo que queramos, y que el operador binario se comporte como queramos. Sin embargo, el operador binario debe ser cerrado, asociativo, y el conjunto debe tener un elemento identidad para que esa estructura algebraica de datos sea un Monoide.
+
+Si restringimos el dominio a todos los subconjuntos de $\set{0,1,2,3,4,5}$ entonces la intersección se convierte claramente en un Monoide porque el elemento identidad sería $\set{0,1,2,3,4,5}$, ya que cualquier conjunto de enteros que se intersecte con él producirá el otro conjunto, es decir, $A ∩ \set{0,1,2,3,4,5} = A$. Por ejemplo, $\set{1,3,4} ∩ \set{0,1,2,3,4,5} = \set{1,3,4}$.
+
+Llegados a este punto debe quedar claro que la categoría de una estructura algebraica para un operador binario dado es muy sensible al dominio del conjunto.
+
+**Ejercicio:** Sea nuestro operador binario la función `min(a,b)` sobre enteros. ¿Se trata de un magma, semigrupo o monoide? ¿Y si restringimos el dominio a enteros positivos (cero o mayor)? ¿Qué pasa con el operador binario `max(a,b)` sobre esos dos dominios?
+
+**Ejercicio:** Sea nuestro conjunto todos los números binarios de 3 bits (un conjunto de cardinalidad 8). Los operadores binarios posibles son y, o, xor, nor, xnor y nand. Es evidente que esto es cerrado porque la salida es un número binario de 3 bits. Para cada operador binario, determinar si el conjunto bajo ese operador binario es un Magma, Semigrupo o Monoide.
+
+## Grupo - La estrella del espectáculo
+
+Un Grupo es un Monoide donde cada elemento tiene un inverso.
+
+O para ser explícitos, es un conjunto con cuatro propiedades:
+
+1. El operador binario es cerrado (Magma)
+2. El operador binario es asociativo (Semigrupo)
+3. El conjunto tiene un elemento identidad (Monoide)
+4. Todo elemento tiene un inverso
+
+Es decir, para cualquier elemento $a$ en el conjunto $A$ , existe un $a′$ tal que $a \square a' = i$ donde $i$ es el elemento identidad y $\square$ es el operador binario. Dicho más matemáticamente, sería:
+
+$$
+\forall a \in A \space\space \exists a' \in A: a\square a' = i
+$$
+
+Aquí, $\square$ es el operador binario del conjunto.
+
+Es bastante incorrecto decir «el conjunto tiene un inverso». Para ser precisos, cada elemento tiene otro elemento en el conjunto que es el inverso de ese elemento.
+
+Usando números enteros con suma, el elemento identidad es cero (porque si sumas cero, obtienes el mismo número), y el inverso de un número entero es ese número entero con el signo invertido (por ejemplo, el inverso de 5 es -5 y el inverso de -7 es 7).
+
+Volviendo a la sensibilidad del dominio, la suma sobre enteros positivos no es un grupo porque no puede haber elementos inversos.
+
+Aquí tienes una tabla para entenderlo
+
+| dominio de conjuntos | operador binario | estructura algebraica | razón |
+| ----------------------------------- | ---------------- | --------------------- | ---------------------------------- |
+| enteros positivos distintos de cero | suma | Semigrupo | sin identidad |
+| enteros positivos incluyendo cero | suma | Monoide | tiene identidad, no tiene inversos |
+| todos los enteros | suma | Grupo | cada elemento tiene un inverso |
+
+Nótese que «inverso» no tiene sentido si el conjunto no tiene identidad, porque la definición de inverso es hacer un operador binario de un elemento con su inverso produce la identidad.
+
+**Ejercicio:** ¿Por qué las cadenas bajo concatenación no pueden ser un conjunto?
+**Ejercicio:** Los polinomios bajo adición satisfacen la propiedad de grupo. Demuestra que es así mostrando que cumple todas las propiedades que definen un grupo.
+
+Desgraciadamente, nuestro tutorial debe terminar aquí, porque la teoría elemental de grupos es el tema de otro capítulo.
+
+Pero ahora tienes mucho contexto para entender qué es un grupo, ¡aunque apenas lo hayamos discutido aquí!
+
+### Unas palabras sobre la conmutatividad
+
+No es necesario que ninguna de las estructuras algebraicas de datos anteriores sea conmutativa. Si lo son, decimos que son abelianas sobre su operador binario. Un grupo abeliano significa que el operador binario no es sensible al orden.
+
+Abeliano significa que el operador binario es conmutativo.
+
+Pero di abeliano, sonarás más inteligente.
+
+El tecnicismo es que normalmente no decimos "la suma es abeliana" sino "el grupo es abeliano sobre la suma".
+
+## Subconjuntos de nuevo
+
+Volvamos a lo que aprendimos al principio. Magmas, Semigrupos, Monoides y Grupos son conjuntos que tienen un operador binario cerrado. Un operador binario no es más que un mapa desde todos los pares ordenados del producto cartesiano del conjunto consigo mismo hacia sí mismo.
+
+Los Grupos son un subconjunto de los Monoides, los Monoides son un subconjunto de los Semigrupos, los Semigrupos son un subconjunto de los Magmas, y los Magmas son un subconjunto de los conjuntos en general. Todo Grupo es también un Magma o un conjunto, pero un Magma no es necesariamente un Grupo.
+
+Los "conjuntos" son fáciles de conceptualizar, pero cuando empezamos a hablar de grupos y otras estructuras algebraicas, es fácil empezar a perderse. Los grupos son muy importantes en nuestro estudio de la criptografía. Recuérdalo:
+
+**Los grupos son conjuntos con un operador binario que sigue cuatro reglas.**
+
+Además, es hora de liberar tu mente de la "suma" y la "multiplicación" como forma principal de combinar cosas.
+
+Se nos permite tomar un producto cartesiano de un conjunto (que puede ser cualquier cosa) consigo mismo y, a continuación, asignar ese conjunto de pares ordenados de nuevo al conjunto. Se trata de un operador binario. Si sigue la construcción anterior, entonces es cerrado.
+
+## El vocabulario matemático no tiene por qué asustarnos
+
+Antes de empezar este tutorial, la frase:
+
+"El conjunto de cadenas sobre el operador binario concatenación de cadenas es un Semigrupo o un Monoide dependiendo de la presencia o ausencia de la cadena vacía en el conjunto"
+
+probablemente no tenía sentido.
+
+Puede que aún tengas que traducirlo en tu cabeza, como la mayoría de los que aprenden un segundo idioma, pero te das cuenta de que en realidad está metiendo mucha información en un espacio minúsculo.
+
+¿Podría decir esa frase sin las matemáticas? Claro que sí, pero necesitaría al menos 500 palabras para hacerlo con claridad. En realidad, merece la pena entender lo que significan esos términos. A la larga nos ahorrará muchos problemas.
+
+Lo que lo hace genial es que hay una plétora de teoremas sobre Grupos que nos permiten hacer afirmaciones sobre el grupo *sin entender cómo funciona el operador binario del grupo bajo el capó*. Esto es muy parecido al polimorfismo en la programación orientada a objetos o a los rasgos en los lenguajes funcionales. Te ocultan los detalles de implementación y te permiten centrarte en el alto nivel. Esto es muy potente.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/arithmetic-circuit_es.md b/spanish-es/arithmetic-circuit_es.md
new file mode 100644
index 0000000..6e6234e
--- /dev/null
+++ b/spanish-es/arithmetic-circuit_es.md
@@ -0,0 +1,675 @@
+# Circuitos aritméticos para ZK
+
+En el contexto de las pruebas de conocimiento-cero, un circuito aritmético es un sistema de ecuaciones que modela un problema en NP.
+
+Un punto clave de nuestro artículo sobre [P vs NP](https://www.rareskills.io/post/p-vs-np) es que cualquier solución a un problema en P o NP puede verificarse modelando el problema como un circuito booleano.
+
+A continuación, convertimos nuestra solución para el problema original en un conjunto de valores para las variables booleanas (llamado el testigo) que da como resultado que el circuito booleano devuelva verdadero.
+
+Este artículo se basa en el anterior, así que léalo primero.
+
+## Circuitos aritméticos como alternativa a los circuitos booleanos
+
+Una desventaja de utilizar un circuito booleano para representar la solución de un problema es que puede resultar prolijo a la hora de representar operaciones aritméticas, como sumas o multiplicaciones.
+
+Por ejemplo, si queremos expresar $a + b = c$ donde $a = 8, b = 4, c = 12$ debemos transformar $a$, $b$ y $c$ en números binarios. Cada bit del número binario corresponderá a una variable booleana distinta. En este ejemplo, supongamos que necesitamos 4 bits para codificar $a$, $b$, y $c$, donde $a₀$ representa el bit menos significativo (LSB), y $a₃$ representa el bit más significativo (MSB) del número $a$, como se muestra a continuación:
+
+- `a₃, a₂, a₁, a₀`
+ - $a = 1000$
+- b₃, b₂, b₁, b₀`
+ - $b = 0100$
+- `c₃, c₂, c₁, c₀`
+ - $c = 1100$
+
+(No hace falta que sepas convertir un número a binario por ahora, explicaremos el método más adelante en el artículo).
+
+Una vez que tenemos $a$, $b$ y $c$ escritos en binario, podemos escribir un circuito booleano cuyas entradas sean todos los dígitos binarios $(a₀, a₁, ..., c₂, c₃)$. Nuestro objetivo es escribir un circuito booleano de este tipo, de forma que el circuito dé como resultado verdadero si y sólo si $a + b = c$.
+
+Esto resulta ser más complicado de lo esperado, como lo demuestra el circuito grande a continuación, que modela $a + b = c$ en binario. Por brevedad, no mostramos la derivación. Sólo mostramos la fórmula para ilustrar lo verboso que puede ser un circuito de este tipo:
+
+```javascript
+((a₄ ∧ b₄ ∧ c₄) ∨ (¬a₄ ∧ ¬b₄ ∧ c₄) ∨ (¬a₄ ∧ b₄ ∧ ¬c₄) ∨ (a₄ ∧ ¬b₄ ∧ ¬c₄) ∧
+
+((a₃ ∧ b₃ ∧ ((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
+ (¬a₃ ∧ ¬b₃ ∧ ((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
+ (¬a₃ ∧ b₃ ∧ ¬((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
+ (a₃ ∧ ¬b₃ ∧ ¬((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))) ∧
+
+((a₂ ∧ b₂ ∧ ((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)) ∨
+ (¬a₂ ∧ ¬b₂ ∧ ((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)) ∨
+ (¬a₂ ∧ b₂ ∧ ¬((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
+ (a₂ ∧ ¬b₂ ∧ ¬((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))) ∧
+
+((a₁ ∧ b₁ ∧ c₀) ∨ (¬a₁ ∧ ¬b₁ ∧ c₀) ∨ (¬a₁ ∧ b₁ ∧ ¬c₀) ∨ (a₁ ∧ ¬b₁ ∧ ¬c₀) ∧
+
+((a₀ ∧ b₀ ∧ c₀) ∨ (¬a₀ ∧ ¬b₀ ∧ c₀) ∨ (¬a₀ ∧ b₀ ∧ ¬c₀) ∨ (a₀ ∧ ¬b₀ ∧ ¬c₀) ∧
+
+¬ ((a₄ ∧ b₄) ∨
+ (b₄ ∧ (a₃ ∧ b₃) ∨ (b₃ ∧ (a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)) ∨
+ (a₃ ∧ (a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))
+```
+
+La cuestión es que, si nos limitamos a entradas booleanas y operaciones booleanas básicas (AND, OR, NOT), la construcción de circuitos puede volverse rápidamente complicada y tediosa para problemas básicos, especialmente cuando implican aritmética.
+
+En cambio, sería más sencillo representar directamente los números dentro de un circuito. En lugar de modelar la suma con una fórmula booleana, utilizamos directamente la suma y la multiplicación en esos números.
+
+Este artículo demuestra que también es posible modelar cualquier problema en P o NP con un *circuito aritmético*.
+
+## Circuitos aritméticos
+
+Un circuito aritmético es un sistema de ecuaciones que sólo utiliza la suma, la multiplicación y la igualdad. Al igual que un circuito booleano, comprueba que un conjunto propuesto de entradas es válido, pero no calcula una solución.
+
+El siguiente es nuestro primer ejemplo de un circuito aritmético:
+
+```javascript
+6 = x₁ + x₂
+9 = x₁x₂
+```
+
+Decimos que un circuito booleano está *satisfecho* si tenemos una asignación a las variables de entrada que resulta en una salida de verdadero. Del mismo modo, un circuito aritmético es satisfecho si hay una asignación a las variables de tal manera que todas las ecuaciones son verdaderas.
+
+Por ejemplo, el circuito anterior se cumple si x₁ = 3, x₂ = 3 porque ambas ecuaciones del circuito son verdaderas. Por el contrario, el circuito no se cumple con `x₁ = 1, x₂ = 6` porque la ecuación `9 = x₁x₂` no es cierta.»
+
+Así pues, podemos pensar indistintamente en un circuito aritmético y en el conjunto de ecuaciones del circuito. Un conjunto de entradas «satisface el circuito» si y sólo si esas entradas hacen que *todas* las ecuaciones sean verdaderas.
+
+## Notación y Terminología
+
+Las variables de un circuito aritmético se denominan **señales** porque [Circom](https://docs.circom.io), el lenguaje de programación que utilizaremos para escribir las Pruebas ZK, se refiere a ellas como tales.
+
+Para expresar igualdad, utilizaremos el operador `===`. Usamos esta notación porque Circom la usa para indicar que dos señales tienen el mismo valor, así que podemos acostumbrarnos a verla.
+
+Hacemos hincapié en que el `===` está afirmando que el lado izquierdo y el lado derecho son iguales. Por ejemplo, en el siguiente circuito
+
+`c === a + b`
+
+**no estamos sumando `a` a `b` y asignando el resultado a `c`**. **En su lugar, suponemos que los valores «a», «b» y «c» se proporcionan como entradas, y estamos afirmando una relación entre ellos. Esto tiene el efecto de «restringir» la suma de «a» y «b» para ser «c».
+
+Piensa que `c === a + b` es completamente equivalente a `assertEq(c, a + b)`. Del mismo modo, la expresión `a + b === c * d` es completamente equivalente a `assertEq(a + b, c * d)`. En esencia, verificar estas ecuaciones en un circuito implica comprobar si se cumplen ciertas condiciones (restricciones). El agente que prueba la validez de su testigo puede asignar cualquier valor a las señales. Sin embargo, su prueba (testigo) sólo se considerará válida si se cumplen todas las restricciones.
+
+Por ejemplo, si un agente desea demostrar:
+
+```javascript
+a === b + c + 3
+a * u === x * y
+```
+
+debe suministrar `(a, b, c, u, x, y)` desde *fuera del circuito* y asignarlas a las señales del circuito.
+
+Recuerda, el código anterior es equivalente a
+
+``javascript
+assertEq(a, b + c + 3)
+assertEq(a * u, x * y)
+
+```
+Un modelo mental útil para el circuito aritmético es que todas las señales se tratan como entradas sin salidas.
+
+Para entenderlo mejor, en el siguiente vídeo se ofrece una visualización. Todas las señales son entradas, y `===` se utiliza para comprobar en lugar de asignar.
+
+
+
+El circuito del vídeo se podría haber escrito como:
+
+```javascript
+z + y === x
+x + y === u
+```
+
+sin cambiar el significado.
+
+El circuito aritmético `x === x + 1` no significa incrementar `x`. Es un circuito aritmético sin solución porque x no puede ser igual a `x + 1`. Por lo tanto, es imposible satisfacer la restricción.
+
+### Interpretación de Circuitos Aritméticos
+
+Considera el siguiente circuito:
+
+```javascript
+x₁(x₁ - 1) === 0
+x₁x₂ === x₁
+```
+
+La primera restricción `x₁(x₁ - 1) === 0` restringe los posibles valores de x₁ a sólo 0 ó 1. Cualquier otro valor de `x₁` no satisfaría esta restricción.
+
+En la segunda restricción `x₁x₂ === x₁` tenemos dos escenarios posibles:
+
+- Si `x₁ = 1`, entonces `x₂` también debe ser 1, o la segunda restricción no se puede satisfacer. Si `x₁ = 1` y `x₂ ≠ 1`, entonces la segunda ecuación se convierte en `1 * x₂ === 1` que sólo puede ser satisfecha por `x₂ = 1`, lo que crea un conflicto.
+- Si `x₁ = 0`, entonces `x₂` puede tener cualquier valor porque `0x₂ === 0` es trivial de satisfacer.
+
+Las siguientes asignaciones a `(x₁, x₂)` son todas testigos válidos:
+
+- $(x₁, x₂) = (1, 1)$
+- $(x₁, x₂) = (0, 2)$
+- $(x₁, x₂) = (0, 1337)$
+- $(x₁, x₂) = (0, 404)$
+
+Recuerda que un sistema de ecuaciones puede tener muchas soluciones. Del mismo modo, un circuito aritmético también puede tener muchas soluciones. Sin embargo, por lo general, sólo estamos interesados en verificar una solución dada. No necesitamos encontrar todas las soluciones de un circuito aritmético.
+
+### Circuito Booleano vs Circuito Aritmético
+
+La siguiente tabla muestra en qué se diferencian los circuitos booleanos y los circuitos aritméticos, pero ten en cuenta que sirven para el mismo propósito de validar un testigo:
+
+| Circuito Booleano | Circuito Aritmético |
+| --------------------------------------------------------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------- |
+| Las variables son 0, 1 | Las señales contienen números |
+| Las únicas operaciones son AND, OR, NOT | Las únicas operaciones son suma y multiplicación |
+| Se cumple cuando la salida es verdadera Se cumple cuando el lado izquierdo es igual al lado derecho para todas las ecuaciones (no hay salida) | |
+| Testigo es una asignación a las variables booleanas que satisface el circuito booleano | Testigo es una asignación a las señales que satisface todas las restricciones de igualdad |
+
+Aparte de la conveniencia de utilizar menos variables en algunas circunstancias, los circuitos aritméticos y los circuitos booleanos son herramientas que realizan el mismo trabajo: demostrar que se tiene un testigo para un problema en NP.
+
+### Volviendo al ejemplo inicial a + b = c
+
+Volvamos a nuestro ejemplo anterior: escribir un circuito *Booleano* para representar la ecuación `a + b = c`, donde se nos da `c = 12`. Para un circuito booleano, necesitamos codificar «a», «b» y «c» en binario, lo que requiere 4 bits cada uno (en este ejemplo). En total, tenemos 12 entradas en el circuito. En comparación, el circuito aritmético sólo requiere 3 entradas: `a`, `b` y `c`. La reducción en el número de entradas y el tamaño total del circuito es la razón por la que preferimos utilizar circuitos aritméticos para aplicaciones ZK.
+
+### Similitudes entre sistemas de ecuaciones y circuitos aritméticos
+
+Los circuitos booleanos siempre tienen una expresión que devuelve verdadero o falso si se satisface el testigo.
+
+Por ejemplo, si tenemos un conjunto de señales $x$, $y$, y $z$, y deseamos restringir la suma de $x$ y $y$ para ser $5$, entonces necesitamos una ecuación separada para eso. Cualquier forma en que deseamos restringir z tendría su propia ecuación separada.
+
+Para demostrar que los circuitos aritméticos y los circuitos booleanos son equivalentes, más adelante demostraremos que cualquier circuito booleano puede transformarse en un circuito aritmético. Esto demuestra que se pueden utilizar indistintamente con el fin de demostrar que un agente tiene un testigo para un problema en P o NP.
+
+### Todos los problemas P son un subconjunto de los problemas NP
+
+Como se discutió en el anterior [capítulo sobre P vs NP](https://www.rareskills.io/post/p-vs-np), **todos los problemas P son un subconjunto de los problemas NP** en términos de los requisitos de cálculo para validar un testigo, por lo que en adelante sólo nos referiremos a problemas NP, entendiendo que esto incluye a P.
+
+Nuestra conclusión es que si cualquier solución a un problema en NP puede modelarse con un circuito booleano, entonces cualquier solución a un problema en NP (o P) puede modelarse con un circuito aritmético.
+
+Pero antes de demostrar su equivalencia, vamos a proporcionar ejemplos de modelado de las soluciones a los problemas en NP para que tengamos una intuición de cómo se utilizan los circuitos aritméticos.
+
+## Ejemplos de circuitos aritméticos
+
+En nuestro primer ejemplo, rehacemos nuestro problema de 3 colores para Australia. En el segundo, demostramos cómo usar un circuito aritmético para probar que una lista está ordenada.
+
+### Ejemplo 1: Modelado de 3 colores con un circuito aritmético
+
+Cuando usamos un circuito Booleano para modelar un 3-color, cada territorio tenía 3 variables Booleanas - una para cada color - indicando si el país había sido asignado ese color. Luego añadimos restricciones para forzar que cada territorio tenga exactamente un color (restricciones de color) y restricciones para forzar que los territorios adyacentes no tengan el mismo color (restricciones de límite).
+
+Es más fácil modelar este problema utilizando circuitos aritméticos porque podemos asignar una sola señal a cada territorio con los posibles valores $\set{1, 2, 3}$ para modelar sus colores, en lugar de tres variables booleanas. Podemos asignar arbitrariamente colores a los números, como `azul = 1`, `rojo = 2`, y `verde = 3`.
+
+Para cada territorio, escribimos la restricción de color único como:
+
+``javascript
+0 === (1 - x) * (2 - x) * (3 - x)
+
+```
+para que cada territorio tenga exactamente un color. La restricción anterior sólo puede cumplirse si «x» es 1, 2 ó 3.
+
+**3-Colorear Australia**
+
+
+
+Recordemos que Australia tiene seis territorios:
+
+- `WA` = Australia Occidental
+- `SA` = Australia Meridional
+- NT = Territorio del Norte
+- Q = Queensland
+- NSW` = Nueva Gales del Sur
+- V = Victoria
+
+Decir `WA = 1` equivale a decir «Colorea de azul Australia Occidental». Del mismo modo, `WA = 2` significa que se asignó «rojo» a Australia Occidental, y `WA = 3` significa que se asignó «verde».
+
+Nuestra restricción de color (restringir cada territorio a ser azul, rojo o verde) para cada territorio se convierte en:
+
+``javascript
+1) 0 === (1 - WA) * (2 - WA) * (3 - WA)
+2) 0 === (1 - SA) * (2 - SA) * (3 - SA)
+3) 0 === (1 - NT) * (2 - NT) * (3 - NT)
+4) 0 === (1 - Q) * (2 - Q) * (3 - Q)
+5) 0 === (1 - NSW) * (2 - NSW) * (3 - NSW)
+6) 0 === (1 - V) * (2 - V) * (3 - V)
+```
+
+Ahora queremos que los territorios vecinos no tengan el mismo color. Una forma de conseguirlo es multiplicar las señales de los territorios vecinos y asegurarnos de que el producto es «aceptable». Considere la siguiente tabla para los territorios vecinos `x` y `y`:
+
+| x | y | product |
+| --- | --- | ---------------------------------- |
+| 1 | 1 | 1 |
+| 1 | 2 | 2 |
+| 1 | 3 | 3 |
+| 2 | 1 | 2 |
+| 2 | 2 | 4 |
+| 2 | 3 | 6 |
+| 3 | 1 | 3 |
+| 3 | 2 | 6 |
+| 3 | 3 | 9 |
+
+If two signals (neighboring territories) have the same number (color), then their product will be one of $\set{1,4,9}$, the red numbers above. If `x` and `y` are constrained to be 1, 2, or 3, and `x` and `y` are not equal to each other, then the product `xy` will be one of $\set{2, 3, 6}$. Therefore, if `xy = 2` or `xy = 3` or `xy = 6`, we accept the assignment because it means the two neighbors have different colors.
+
+For each neighboring territory `x` and `y`, we can use the following constraint to enforce that they are not equal to each other:
+
+```javascript
+0 === (2 - xy) * (3 - xy) * (6 - xy)
+```
+
+La ecuación anterior se cumple si y sólo si el producto `xy` es igual a 2, 3 ó 6.
+
+Las restricciones de contorno se crean iterando a través de los bordes y aplicando las restricciones de contorno entre cada par de territorios vecinos como ilustra el siguiente vídeo:
+
+
+
+Ahora mostramos las restricciones de límites:
+
+```javascript
+Australia Occidental y Australia Meridional:
+7) 0 === (2 - WA * SA) * (3 - WA * SA) * (6 - WA * SA)
+
+Australia Occidental y Territorio del Norte
+8) 0 === (2 - WA * NT) * (3 - WA * NT) * (6 - WA * NT)
+
+Territorio del Norte y Australia Meridional
+9) 0 === (2 - NT * SA) * (3 - NT * SA) * (6 - NT * SA)
+
+Territorio del Norte y Queensland
+10) 0 === (2 - NT * Q) * (3 - NT * Q) * (6 - NT * Q)
+
+Australia Meridional y Queensland
+11) 0 === (2 - SA * Q) * (3 - SA * Q) * (6 - SA * Q)
+
+Australia Meridional y Nueva Gales del Sur
+12) 0 === (2 - SA * NSW) * (3 - SA * NSW) * (6 - SA * NSW)
+
+Australia Meridional y Victoria
+13) 0 === (2 - SA * V) * (3 - SA * V) * (6 - SA * V)
+
+Queensland y Nueva Gales del Sur
+14) 0 === (2 - Q * NSW) * (3 - Q * NSW) * (6 - Q * NSW)
+
+Nueva Gales del Sur y Victoria
+15) 0 === (2 - NSW * V) * (3 - NSW * V) * (6 - NSW * V)
+```
+
+Combinando los dos, vemos el circuito aritmético completo para probar que tenemos una 3-coloración válida para Australia:
+
+```javascript
+// restricciones de color
+0 === (1 - WA) * (2 - WA) * (3 - WA)
+0 === (1 - SA) * (2 - SA) * (3 - SA)
+0 === (1 - NT) * (2 - NT) * (3 - NT)
+0 === (1 - Q) * (2 - Q) * (3 - Q)
+0 === (1 - NSW) * (2 - NSW) * (3 - NSW)
+0 === (1 - V) * (2 - V) * (3 - V)
+
+// restricciones fronterizas
+0 === (2 - WA * SA) * (3 - WA * SA) * (6 - WA * SA)
+0 === (2 - WA * NT) * (3 - WA * NT) * (6 - WA * NT)
+0 === (2 - NT * SA) * (3 - NT * SA) * (6 - NT * SA)
+0 === (2 - NT * Q) * (3 - NT * Q) * (6 - NT * Q)
+0 === (2 - SA * Q) * (3 - SA * Q) * (6 - SA * Q)
+0 === (2 - SA * NSW) * (3 - SA * NSW) * (6 - SA * NSW)
+0 === (2 - SA * V) * (3 - SA * V) * (6 - SA * V)
+0 === (2 - Q * NSW) * (3 - Q * NSW) * (6 - Q * NSW)
+0 === (2 - NSW * V) * (3 - NSW * V) * (6 - NSW * V)
+```
+
+Tenemos 15 restricciones como en el circuito booleano, **pero 1/3 de variables (señales)**. En lugar de 3 variables booleanas para cada territorio, tenemos una señal para cada territorio. Para circuitos más grandes, esta reducción en complejidad y espacio puede ser sustancial.
+
+### Ejemplo 2: Demostrar que una lista está ordenada
+
+Dada una lista de números `[a₁, a₂, ..., aₙ]`, decimos que la lista está «ordenada» si `aₙ ≥ aₙ₋₁ ≥ ... a₃ ≥ a₂ ≥ a₁`. En otras palabras, yendo del final al principio, los números no son crecientes.
+
+Nuestro objetivo es escribir un circuito aritmético que verifique que la lista está ordenada.
+
+Para ello, necesitamos un circuito aritmético que exprese `a ≥ b` para dos señales. Esto resulta ser más complicado de lo que parece a primera vista, porque los circuitos aritméticos sólo permiten igualdades, sumas y multiplicaciones, no comparaciones.
+
+Pero supongamos que tenemos un circuito «mayor o igual que» -llamémoslo `GTE(a,b)`. Entonces construiríamos los circuitos para comparar cada par de elementos consecutivos de la lista: `GTE(aₙ, aₙ₋₁), ..., GTE(a₃, a₂), GTE(a₂, a₁)`, y si se cumplen todos, entonces se ordena la lista.
+
+Para comparar dos números decimales sin el operador $≥$, primero necesitamos un circuito aritmético que valide una representación binaria propuesta para el número, así que primero damos un pequeño rodeo sobre los números binarios.
+
+### Prerrequisito: Codificación binaria
+
+Escribimos los números binarios con el subíndice 2. Por ejemplo, 11₂ es 3 y 101₂ es 5. Cada uno de los 1s y 0s se denomina bit. Decimos que el bit situado más a la izquierda es el bit más significativo (MSB) y el situado más a la derecha es el bit menos significativo (LSB).
+
+Como veremos en breve, durante la conversión a decimal, el bit más significativo se multiplica por el coeficiente mayor y el bit menos significativo se multiplica por el coeficiente menor. Así, si escribimos un número binario de cuatro bits como `b₃b₂b₁b₀`, `b₃` es el MSB y `b₀` es el LSB.
+
+El siguiente vídeo ilustra la conversión de 1101₂ a 13:
+
+
+
+Como se muestra en el video, un número binario de cuatro bits se puede convertir a un número decimal `v` con la siguiente fórmula:
+
+`v = 8b₃ + 4b₂ + 2b₁ + b₀`
+
+Esto también podría escribirse como:
+
+`v = 2³b₃ + 2²b₂ + 2¹b₁ + 2⁰b₀`.
+
+Por ejemplo, 1001₂ = 9, 1010₂ = 10, y así sucesivamente. Para un número binario general de `n` bits, la conversión es:
+
+`v = 2ⁿ-¹b₃ + ... + 2¹b₁ + 2⁰b₀`
+
+Omitimos la discusión sobre cómo convertir un número decimal a binario. Por ahora, si el lector desea convertir a binario, puede utilizar la función incorporada `bin` de Python:
+
+```javascript
+>>> bin(3)
+'0b11'
+>>> bin(9)
+'0b1001'
+>>> bin(10)
+'0b1010'
+>>> bin(1337)
+'0b10100111001'
+>>> bin(404)
+'0b110010100'
+```
+
+Podemos crear un circuito aritmético que afirme «`v` es un número decimal con una representación binaria de cuatro bits `b₃`, `b₂`, `b₁`, `b₀`» utilizando el siguiente circuito:
+
+```javascript
+8b₃ + 4b₂ + 2b₁ + b₀ === v
+
+// forzar a que los «bits» sean cero o uno.
+b₀(b₀ - 1) === 0
+b₁(b₁ - 1) === 0
+b₂(b₂ - 1) === 0
+b₃(b₃ - 1) === 0
+```
+
+Las señales `b₃, b₂, b₁, b₀` están limitadas a ser la representación binaria de `v`. Si `b₃, b₂, b₁, b₀` no son binarios, o no son la representación binaria de `v`, entonces el circuito no se puede satisfacer.
+
+Observe que **no hay ninguna asignación satisfactoria a las señales `(v, b₃, b₂, b₁, b₀)` donde `v > 15`.** Es decir, si ponemos `b₃, b₂, b₁, b₀` a todos 1, lo más alto que permiten las restricciones, entonces la suma será 15. No es posible sumar nada más alto. En ZK, esto se llama a veces una *comprobación de rango* en `v`. El circuito anterior no sólo demuestra la representación binaria de `v`, sino que también obliga a que `v < 16`.
+
+Podemos generalizar esto al siguiente circuito que obliga a $v < 2^n$ y también nos da la representación binaria de `v`:
+
+```javascript
+2ⁿ-¹bₙ₋₁ +...+ 2²b₂ + 2¹b₁ + b₀ === v
+b₀(b₀ - 1) === 0
+b₁(b₁ - 1) === 0
+//...
+bₙ₋₁(bₙ₋₁ - 1) === 0
+```
+
+**Decir que un número `v` está codificado con un máximo de `n` bits equivale a decir $v < 2^n$.**
+
+Para hacerse una idea de cómo cambia $2^n$ en función de $n$, considere la siguiente tabla:
+
+| n bits | valor máximo (binario) | valor máximo (decimal) | 2ⁿ (decimal) | 2ⁿ (binario) |
+| ------ | ---------------------- | ---------------------- | ------------ | ------------ |
+| 2 | 11₂ | 3 | 4 | 100 |
+| 3 | 111₂ | 7 | 8 | 1000 |
+| 4 | 1111₂ | 15 | 16 | 10000 |
+| 5 | 11111₂ | 31 | 32 | 100000 |
+
+Observe que el número $2^n$ en binario requiere 1 bit más para almacenarse que el valor $2^n - 1$. Al restringir el número de bits con los que se codifica un número a $n$ bits, se fuerza a que ese número sea menor que $2^n$.
+
+Es útil recordar la relación entre potencias de $2$ y el número de bits necesarios para almacenarlas.
+
+- $2^n$ requiere $n + 1$ bits para almacenarse. Por ejemplo, $2^0=1_2$, $2^1 = 10_2$, $2^2=100_2$, $2^3=1000_2$ y así sucesivamente.
+- $2^{n-1}$ es la mitad de $2^n$ y requiere $n$ bits para almacenar
+- $2^n - 1$ requiere $n$ bits para almacenar. Es el valor máximo que podemos almacenar con $n$ bits, cuando todos los bits están a $1$.
+
+Si tomamos un número $n$ y calculamos $2^n$, obtenemos un número de $n + 1$ bits con el bit más significativo a 1, y el resto a cero. $n = 3$ en los ejemplos siguientes:
+
+$$
+2^n=\underbrace{1000}_{n+1\space bits}
+$$
+
+$2^{n-1}$ es lo mismo que $2^n / 2$. Puesto que se escribe como 2 a alguna potencia, sigue teniendo la misma «forma» de un número binario con un MSB de 1 y el resto cero, pero requerirá $n$ bits para codificarlo en lugar de $n + 1$ bits.
+
+$$
+2^{n-1}=\underbrace{100}_{n\space bits}
+$$
+
+$2^n -1$ es un número de $n$ bits con todos los bits a uno.
+
+$$
+2^n-1=\underbrace{111}_{n\space bits}
+$$
+
+### Calcular ≥ en binario
+
+Si trabajamos con números binarios de un tamaño fijo, $n$ bits, el número $2^{n-1}$ es especial porque podemos afirmar fácilmente que un número binario de $n$ bits es mayor o igual que $2^{n-1}$ - o menor que él. Llamamos $2^{n-1}}$ al «punto medio». El siguiente vídeo ilustra cómo comparar el tamaño de un número de $n$ bits con $2^{n-1}$:
+
+
+
+Comprobando el bit más significativo de un número de $n$ bits, podemos saber si ese número es mayor o igual que $2^{n-1}$ o menor que $2^{n-1}$.
+
+Si calculamos $2^{n-1} + \Delta$ y miramos el bit más significativo de esa suma, podemos saber rápidamente si $\Delta$ es positivo o negativo. Si $\Delta$ es negativo, entonces $2^{n-1} + \Delta$ debe ser menor que $2^{n-1}$.
+
+
+
+### Detectar si $u \ge v$
+
+Si sustituimos $\Delta$ por $u - v$ entonces el bit más significativo de $2^{n-1} + (u - v)$ nos dice si $u ≥ v$ o $u < v$.
+
+
+
+#### Prevención del desbordamiento en $2^{n-1} + (u - v)$
+
+Si restringimos $u$ y $v$ para que se representen con un máximo de $n - 1$ bits, mientras que $2^{n-1}$ se representa con $n$ bits, entonces no pueden producirse subdesbordamiento ni desbordamiento. Cuando ambos $u$ y $v$ se representan con un máximo de $n - 1$ bits, el valor absoluto máximo de $|u - v|$ es un número de $n - 1$ bits.
+
+Vemos que $2^{n-1} + (u - v)$ no puede desbordarse en este caso, porque $2^{n-1}$ es al menos 1 bit mayor que $|u - v|$.
+
+Consideremos ahora el caso de desbordamiento. Sin pérdida de generalidad, para $n = 4$, es decir, números de cuatro bits, el punto medio es $2^{n-1} = 2^{4-1} = 8$ o $1000_2$. El valor máximo que puede tener $|u - v|$ en este caso, como número de 3 bits, es $111_2$. Sumando $1000_2 + 111_2$ se obtiene $1111_2$, que no es un desbordamiento.
+
+### Resumen del circuito aritmético para $u ≥ v$, cuando $u$ y $v$ son números de $n - 1$ bits.
+
+- Restringimos $u$ y $v$ a ser como máximo números de $n - 1$ bits.
+- Creamos un circuito aritmético que codifica la representación binaria de $2^{n-1} + (u - v)$ utilizando $n$ bits.
+- Si el bit más significativo de $2^{n-1} + (u - v)$ es 1, entonces $u \geq v$ y viceversa.
+
+El circuito aritmético final para comprobar si $u \geq v$ es el siguiente. Fijamos $n = 4$, lo que significa que $u$ y $v$ deben ser números de 3 bits. El lector interesado puede generalizar esto a otros valores de $n$:
+
+```javascript
+// u y v se representan con un máximo de 3 bits:
+2²a₂ + 2¹a₁ + a₀ === u
+2²b₂ + 2¹b₁ + b₀ === v
+
+// 0 1 restricciones para aᵢ, bᵢ
+a₀(a₀ - 1) === 0
+a₁(a₁ - 1) === 0
+a₂(a₂ - 1) === 0
+b₀(b₀ - 1) === 0
+b₁(b₁ - 1) === 0
+b₂(b₂ - 1) === 0
+
+// 2ⁿ⁻¹ + (u - v) representación binaria
+2³ + (u - v) === 8c₃ + 4c₂ + 2c₁ + c₀
+
+// 0 1 restricciones para cᵢ
+c₀(c₀ - 1) === 0
+c₁(c₁ - 1) === 0
+c₂(c₂ − 1) === 0
+c₃(c₃ − 1) === 0
+
+// Verificar que el MSB sea 1
+c₃ === 1
+```
+
+### Afirmar que una lista está ordenada
+
+Ahora que tenemos un circuito aritmético para comparar pares de señales, repetimos este circuito para cada par secuencial en la lista y verificamos que esté ordenado.
+
+## Resumen de ejemplos
+
+Hemos mostrado cómo podemos crear un circuito aritmético que modele la solución a los problemas del capítulo anterior.
+
+Ahora podemos generalizar esto para decir que podemos modelar cualquier problema en NP usando un circuito aritmético.
+
+## Cómo se puede modelar un circuito booleano con un circuito aritmético
+
+Cualquier circuito booleano se puede modelar utilizando un circuito aritmético. Esto significa que podemos definir un proceso para convertir un circuito booleano B en un circuito aritmético A, de modo que un conjunto de entradas que satisfacen B se pueda traducir en un conjunto de señales que satisfacen A. A continuación, describimos los componentes clave de este proceso y analizamos un ejemplo de conversión de un circuito booleano específico en un circuito aritmético.
+
+Supongamos que tenemos la siguiente fórmula booleana: `out = (x ∧ ¬ y) ∨ z`. Esta fórmula es verdadera si (`x` es verdadera Y `y` es falsa) O `z` es verdadera.
+
+Codificamos `x`, `y` y `z` como señales de circuito aritmético y las restringimos a tener valores 0 o 1.
+
+El siguiente circuito aritmético solo se puede satisfacer si `x`, `y` y `z` son cada uno 0 o 1.
+
+```javascript
+x(x - 1) === 0
+y(y - 1) === 0
+z(z - 1) === 0
+```
+
+Ahora, mostremos cómo mapear operadores de circuito booleanos a operadores de circuito aritmético, suponiendo que las variables de entrada han sido restringidas a ser 0 o 1.
+
+### Puerta AND
+
+Traducimos el AND booleano `t = u ∧ v` a un circuito aritmético de la siguiente manera:
+
+```javascript
+u(u - 1) === 0
+v(v - 1) === 0
+t === uv
+```
+
+`t` solo será 1 si tanto `u` como `v` son 1, por lo tanto, este circuito aritmético modela una compuerta AND. Debido a las restricciones `u(u - 1) = 0` y `v(v - 1) = 0`, `t` solo puede ser 0 o 1.
+
+### Puerta NOT
+
+Traducimos la función NOT booleana `t = ¬u` a un circuito aritmético de la siguiente manera:
+
+```javascript
+u(u - 1) === 0
+t === 1 - u
+```
+
+`t` es 1 cuando `u` es 0 y viceversa. Debido a la restricción `u(u - 1) === 0`, `t` solo puede ser 0 o 1.
+
+### Puerta OR
+
+Traducimos la función OR booleana `t === u ∨ v` a un circuito aritmético de la siguiente manera:
+
+```javascript
+u(u - 1) === 0
+v(v - 1) === 0
+t === u + v - uv
+```
+
+Para ver por qué modela la puerta OR, considere la siguiente tabla:
+
+| u | v | u + v | uv | t (u + v - uv) |
+| --- | --- | ----- | --- | -------------- |
+| 0 | 0 | 0 | 0 | 0 |
+| 0 | 1 | 1 | 0 | 1 |
+| 1 | 0 | 1 | 0 | 1 |
+| 1 | 1 | 2 | 1 | 1 |
+
+Si `u` o `v` son 1, entonces `t` será al menos 1. Para evitar que `t` sea igual a 2 (que es una salida no válida de un operador booleano), restamos `uv`, que será 1 cuando tanto `u` como `v` sean 1.
+
+Observe que con todas las puertas anteriores, no necesitamos aplicar una restricción `t(t - 1) === 0`. La salida `t` está implícitamente restringida a ser 0 o 1 porque no hay ninguna asignación a las entradas que pueda resultar en un valor 2 o mayor para `t`.
+
+### Transformando `out = (x ∧ ¬ y) ∨ z` en un circuito aritmético
+
+Ahora que hemos visto cómo traducir todas las operaciones permitidas de los circuitos booleanos en circuitos aritméticos, veamos un ejemplo de conversión de un circuito booleano en uno aritmético.
+
+### Crea las restricciones 0 1
+
+```javascript
+x(x - 1) === 0
+y(y - 1) === 0
+z(z - 1) === 0
+```
+
+### Reemplaza `¬ y` con el circuito aritmético para NOT
+
+out = (x ∧ ¬ y) ∨ z
+
+out = (x ∧ (1 - y)) ∨ z
+
+### Reemplaza `∧` con el circuito aritmético para AND
+
+out = (x ∧ (1 - y)) ∨ z
+
+out = (x(1 - y)) ∨ z
+
+### Reemplaza `∨` con el circuito aritmético para OR
+
+out = (x(1 - y)) ∨ z
+
+out = (x(1 - y)) + z - (x(1 - y))z
+
+Nuestro circuito aritmético final para `out = (x ∧ ¬ y) ∨ z` es:
+
+```javascript
+x(x - 1) === 0
+y(y - 1) === 0
+z(z - 1) === 0
+out === (x(1 - y)) + z - (x(1 - y))z
+```
+
+Si se desea, podemos simplificar la última ecuación:
+
+```javascript
+out === (x(1 - y)) + z - ((x(1 - y))z)
+out === x - xy + z - ((x - xy)z)
+out === x - xy + z - (xz - xyz)
+
+out === x - xy + z - xz + xyz
+```
+
+También podemos escribir el circuito aritmético de la siguiente manera sin cambiar el significado:
+
+```javascript
+x² === x
+y² === y
+z² === z
+out === x - xy + z - xz + xyz
+```
+
+## Resumen
+
+**Si la solución de cada problema en NP se puede modelar con un circuito booleano y cada circuito booleano se puede transformar en un circuito aritmético equivalente, entonces se deduce que la solución de cada problema en El NP se puede modelar con un circuito aritmético.**
+
+En la práctica, los desarrolladores de ZK prefieren utilizar circuitos aritméticos en lugar de circuitos booleanos porque, como se muestra en los ejemplos anteriores, generalmente requieren menos variables para lograr la misma tarea.
+
+No es necesario calcular un circuito booleano y luego transformarlo en un circuito aritmético. Podemos modelar la solución al problema NP con un circuito aritmético directamente.
+
+## Próximos pasos
+
+Hemos pasado por alto dos detalles muy importantes en este artículo. Existen otros desafíos que deben abordarse. Por ejemplo:
+
+- No analizamos qué tipo de datos usamos para almacenar señales para el circuito aritmético y cómo manejamos el desbordamiento durante la suma o la multiplicación.
+- No tenemos forma de expresar el valor 2/3 sin perder precisión. Cualquier representación de punto fijo o punto flotante que elijamos tendrá problemas de redondeo.
+
+Para manejar estos problemas, los circuitos aritméticos se calculan sobre *[campos finitos](rareskills.io/post/finite-fields):* una rama de las matemáticas donde toda la suma y multiplicación se realiza módulo un número primo.
+
+La aritmética de campos finitos tiene algunas diferencias sorprendentes con la aritmética regular introducida por el operador módulo, por lo que el próximo capítulo las explorará en detalle.
+
+## Obtenga más información con RareSkills
+
+Obtenga más información sobre [Pruebas de conocimiento cero](https://www.rareskills.io/zk-book) en nuestro libro gratuito ZK. Este tutorial es un capítulo de ese libro.
+
+## Problemas de práctica
+
+1. Cree un circuito aritmético que tome las señales `x₁`, `x₂`, ..., `xₙ` y se satisfaga si *al menos* una señal es 0.
+
+2. Cree un circuito aritmético que tome las señales `x₁`, `x₂`, ..., `xₙ` y se satisfaga si todas las señales son 1.
+
+3. Un gráfico bipartito es un gráfico que se puede colorear con dos colores de modo que ningún nodo vecino comparta el mismo color. Diseñe un esquema de circuito aritmético para demostrar que tiene un testigo válido de una coloración doble de un gráfico. Sugerencia: el esquema de este tutorial debe ajustarse antes de que funcione con un coloreado de 2 colores.
+
+4. Cree un circuito aritmético que restrinja `k` para que sea el máximo de `x`, `y` o `z`. Es decir, `k` debe ser igual a `x` si `x` es el valor máximo, y lo mismo para `y` y `z`.
+
+5. Cree un circuito aritmético que tome las señales `x₁`, `x₂`, ..., `xₙ`, las restrinja para que sean binarias y genere 1 si *al menos* una de las señales es 1. Sugerencia: esto es más complicado de lo que parece. Considere combinar lo que aprendió en los primeros dos problemas y usar la compuerta NOT.
+
+6. Crea un circuito aritmético para determinar si una señal `v` es una potencia de dos (1, 2, 4, 8, etc.). Sugerencia: crea un circuito aritmético que restrinja otro conjunto de señales para codificar la representación binaria de `v`, luego coloca restricciones adicionales en esas señales.
+
+7. Crea un circuito aritmético que modele el [problema de suma de subconjuntos](https://en.wikipedia.org/wiki/Subset_sum_problem). Dado un conjunto de números enteros (supón que todos son no negativos), determina si hay un subconjunto que sume un valor dado $k$. Por ejemplo, dado el conjunto $\set{3,5,17,21}$ y $k = 22$, hay un subconjunto $\set{5, 17}$ que suma $22$. Por supuesto, un problema de suma de subconjuntos no necesariamente tiene una solución.
+
+
+ Sugerencia
+
+ Utilice un "cambio" que sea 0 o 1 si un número es parte del subconjunto o no.
+
+
+8. El problema del conjunto de recubrimiento comienza con un conjunto $S = \set{1, 2, …, 10}$ y varios subconjuntos bien definidos de $S$, por ejemplo: $\set{1, 2, 3}$, $\set{3, 5, 7, 9}$, $\set{8, 10}$, $\set{5, 6, 7, 8}$, $\set{2, 4, 6, 8}$, y pregunta si podemos tomar como máximo $k$ subconjuntos de $S$ tales que su unión sea $S$. En el problema de ejemplo anterior, la respuesta para $k = 4$ es verdadera porque podemos usar $\set{1, 2, 3}$, $\set{3, 5, 7, 9}$, $\set{8, 10}$, $\set{2, 4, 6, 8}$. Tenga en cuenta que para cada problema, los subconjuntos con los que podemos trabajar se determinan al principio. No podemos construir los subconjuntos nosotros mismos. Si nos hubieran dado los subconjuntos $\set{1,2,3}$, $\set{4,5}$ $\set{7,8,9,10}$ entonces no habría solución porque el número $6$ no está en los subconjuntos.
+
+Por otra parte, si nos hubieran dado $S = \set{1,2,3,4,5}$ y los subconjuntos $\set{1}, \set{1,2}, \set{3, 4}, \set{1, 4, 5}$ y nos hubieran preguntado si se puede cubrir con $k = 2$ subconjuntos, entonces no habría solución. Sin embargo, si $k = 3$ entonces una solución válida sería $\set{1, 2}, \set{3, 4}, \set{1, 4, 5}$.
+
+Nuestro objetivo es demostrar para un conjunto dado $S$ y una lista definida de subconjuntos de $S$, si podemos elegir un conjunto de subconjuntos tales que su unión sea $S$. Específicamente, la pregunta es si podemos hacerlo con $k$ o menos subconjuntos. Deseamos demostrar que sabemos qué $k$ (o menos) subconjuntos usar codificando el problema como un circuito aritmético.
+
+*Publicado originalmente el 23 de abril de 2024*
diff --git a/spanish-es/bilinear-pairing_es.md b/spanish-es/bilinear-pairing_es.md
new file mode 100644
index 0000000..dfa44d4
--- /dev/null
+++ b/spanish-es/bilinear-pairing_es.md
@@ -0,0 +1,596 @@
+# Emparejamientos bilineales en Python, Solidity y EVM
+
+A veces también llamados mapeos bilineales, los emparejamientos bilineales nos permiten tomar tres números, $a$, $b$ y $c$, donde $ab = c$, cifrarlos para convertirlos en $E(a)$, $E(b)$, $E(c)$, donde $E$ es una función de cifrado, y luego enviar los dos valores cifrados a un verificador que puede verificar $E(a)E(b) = E(c)$ pero no conocer los valores originales. Podemos usar emparejamientos bilineales para demostrar que un tercer número es el producto de los dos primeros sin conocer los dos primeros números originales.
+
+Explicaremos los emparejamientos bilineales a un alto nivel y brindaremos algunos ejemplos en Python.
+
+## Requisitos previos
+
+- El lector debe saber qué son la [suma de puntos](https://www.rareskills.io/post/elliptic-curve-addition) y la multiplicación escalar en el contexto de las curvas elípticas.
+- El lector también debe conocer el problema del logaritmo discreto en este contexto: un escalar multiplicado por un punto dará como resultado otro punto, y en general no es factible calcular el escalar dado el punto de la curva elíptica.
+- El lector debe saber qué son un [campo finito](rareskills.io/post/finite-fields) y un grupo cíclico, y qué es un generador en el contexto de las curvas elípticas. Nos referiremos a los generadores con la variable G.
+- El lector debe saber sobre las [precompilaciones de Ethereum](https://www.rareskills.io/post/solidity-precompiles).
+ Usaremos letras mayúsculas para denotar puntos de EC (curva elíptica) y letras minúsculas para denotar elementos de campos finitos ("escalares"). Cuando decimos elemento, este podría ser un número entero en un campo finito o podría ser un punto en una curva elíptica. El contexto lo aclarará.
+
+Es posible leer este tutorial sin comprender completamente todo lo anterior, pero será más difícil desarrollar una buena intuición sobre este tema.
+
+## Cómo funcionan los emparejamientos bilineales
+
+Cuando un escalar se multiplica por un punto en una curva elíptica, se produce otro punto de la curva elíptica. Es decir, $P = pG$, donde $p$ es un escalar y $G$ es el generador. Dados $P$ y $G$, no podemos determinar $p$.
+
+Supongamos que $pq = r$. Lo que estamos tratando de hacer es tomar
+
+$$
+\begin{align*}
+P = pG\\
+Q = qG\\
+R = rG\\
+\end{align*}
+$$
+
+y convencer a un verificador de que los logaritmos discretos de $P$ y $Q$ se multiplican para producir el logaritmo discreto de $R$.
+
+Si $pq = r$, y $P = pG$, $Q = qG$, y $R = rG$, entonces queremos una función tal que
+
+$$f(P,Q)=R$$
+
+y no sea igual a $R$ cuando $pq ≠ r$. Esto debería ser cierto para todas las combinaciones posibles de $p$, $q$, y $r$ en el grupo.
+
+Sin embargo, normalmente no es así como expresamos $R$ cuando usamos emparejamientos bilineales. Por razones que analizaremos más adelante, normalmente se calcula como
+
+$$f(P,Q) = f(R,G)$$
+
+$G$ es el punto generador y se puede considerar como $1$. En este contexto, por ejemplo, $pG$ significa que hicimos $(G + G + … + G)$ $p$ veces. $G$ simplemente significa que tomamos $G$ y no agregamos nada. Por lo tanto, en cierto sentido, esto es lo mismo que decir $P
+\times Q = R \times 1$.
+
+Por lo tanto, nuestro emparejamiento bilineal es una función que, si se introducen dos puntos de la curva elíptica, se obtiene una salida que *corresponde* al producto de los logaritmos discretos de esos dos puntos.
+
+### Notación
+
+Un emparejamiento bilineal normalmente se escribe como $e(P, Q)$. Aquí, $e$ no tiene nada que ver con el logaritmo natural, y $P$ y $Q$ son puntos de la curva elíptica.
+
+### Generalización, comprobación de si dos productos son iguales
+
+Supongamos que alguien nos dio cuatro puntos de curva elíptica $P_1$, $P_2$, $Q_1$ y $Q_2$ y afirmó que los logaritmos discretos de $P_1$ y $P_2$ tienen el mismo producto que $Q_1$ y $Q_2$, es decir, $p_1p_2 = q_1q_2$. Usando un emparejamiento bilineal, podemos comprobar si esto es cierto sin saber $p_1$, $p_2$, $q_1$ o $q_2$. Simplemente hacemos:
+
+$$e(P_1, P_2) \stackrel{?}{=} e(Q_1, Q_2)$$
+
+### Qué significa "bilineal"
+
+Bilineal significa que si una función toma dos argumentos, y uno de ellos se mantiene constante y el otro varía, entonces el resultado varía linealmente con el argumento no constante.
+
+Si $f(x,y)$ es bilineal y $c$ es constante, entonces $z = f(x, c)$ varía linealmente con $x$ y $z = f(c, y)$ varía linealmente con $y$.
+
+De esto podemos inferir que un emparejamiento bilineal de curva elíptica tiene la siguiente propiedad:
+
+$$
+f(aG, bG) = f(abG, G) = f(G, abG)
+$$
+
+### ¿Qué devuelve $e(P, Q)$?
+Para ser honestos, el resultado es tan matemáticamente aterrador que sería contraproducente tratar de explicarlo realmente. Por eso, gran parte del libro anterior dedicó mucho tiempo a explicar los grupos, porque es exponencialmente más fácil entender qué es un grupo que entender qué devuelve $e(P, Q)$.
+
+La salida de un emparejamiento bilineal es un elemento de grupo, específicamente un elemento de un grupo cíclico finito.
+
+**Es mejor tratar a $e(P, Q)$ como una caja negra** de forma similar a cómo la mayoría de los programadores tratan las funciones hash como cajas negras.
+
+Sin embargo, a pesar de ser una caja negra, todavía sabemos mucho sobre las propiedades de la salida, a la que llamamos $G_T$:
+
+- $G_T$ es un grupo cíclico, por lo que tiene un operador binario cerrado.
+- El operador binario de $G_T$ es asociativo.
+- $G_T$ tiene un elemento identidad.
+- Cada elemento de $G_T$ tiene una inversa.
+- Debido a que el grupo es cíclico, tiene un generador.
+- Como el grupo es cíclico y finito, los grupos cíclicos finitos son homomórficos a $G_T$. Es decir, tenemos alguna forma de mapear homomórficamente elementos en un cuerpo finito a elementos en $G_T$.
+
+Como el grupo es cíclico, tenemos una noción de $G_T$, $2G_T$, $3G_T$, etc. El operador binario de $G_T$ es aproximadamente lo que llamaríamos "multiplicación", por lo que $8G_T = 2G_T * 4G_T$.
+
+Si realmente quieres saber cómo se ve $G_T$, es un objeto de 12 dimensiones. Sin embargo, el elemento de identidad no tiene un aspecto tan aterrador:
+
+$$(1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)$$
+
+## Grupos simétricos y asimétricos
+
+La notación anterior implica que estamos usando el mismo generador y grupo de curva elíptica en todas partes cuando decimos
+
+$$e(aG, bG) = e(abG, G)$$
+
+Sin embargo, en la práctica resulta más fácil crear emparejamientos bilineales cuando un grupo diferente (pero del mismo orden) es diferente para ambos argumentos.
+
+En concreto, decimos
+
+$$e(a, b) → c, \space\space a ∈ G_1, b ∈ G_2, c ∈ G_T$$
+
+Ninguno de los grupos utilizados es el mismo.
+
+Sin embargo, la propiedad que nos interesa sigue siendo válida.
+
+$$e(aG_1, bG_2) = e(abG_1, G_2) = e(G_1, abG_2)$$
+
+En la ecuación anterior, el grupo $G_T$ no se muestra explícitamente, pero ese es el codominio (espacio de salida) de $e(G_1, G_2)$.
+
+Se podría pensar que $G_1$ y $G_2$ son ecuaciones de curva elíptica diferentes con parámetros diferentes (pero la misma cantidad de puntos) y eso sería válido porque son grupos diferentes.
+
+En un emparejamiento simétrico, se utiliza el mismo grupo de curva elíptica para ambos argumentos de la función de emparejamiento bilineal. Esto significa que el generador y el grupo de curvas elípticas utilizados en ambos argumentos son los mismos. En este caso, la función de emparejamiento se suele denotar como:
+
+$$e(aG_1, bG_1) = e(abG_1, G_1) = e(G_1, abG_1)$$
+
+En un emparejamiento asimétrico, los argumentos utilizan grupos diferentes. Por ejemplo, el primer argumento puede utilizar un generador y un grupo de curvas elípticas diferentes a los del segundo argumento. La función de emparejamiento puede satisfacer las propiedades deseadas
+
+$$e(aG_1, bG_2) = e(abG_1, G_2) = e(G_1, abG_2)$$
+
+En la práctica, utilizamos grupos asimétricos y la diferencia entre los grupos que utilizamos se explica en la siguiente sección.
+
+$G_1$ es el mismo grupo del que hablamos en capítulos anteriores y, en el contexto de Ethereum, es el mismo `G1` que importamos de la biblioteca:
+
+```python
+from py_ecc.bn128 import G1
+```
+
+También podemos importar el `G2` de la misma biblioteca como:
+
+```python
+from py_ecc.bn128 import G1, G2
+```
+
+Pero, ¿qué es $G_2$?
+
+## Extensiones de campo y el punto `G2` en Python
+
+Los emparejamientos bilineales son bastante independientes de los tipos de grupos que elija, pero $G_2$ de Ethereum usa curvas elípticas con extensiones de campo. Si quieres poder leer el código de Solidity que utiliza ZK-SNARKS, necesitarás al menos una idea aproximada de lo que son.
+
+Normalmente pensamos en los puntos EC como dos puntos $x$ e $y$. Con las *extensiones de campo*, los $x$ e $y$ se convierten en objetos bidimensionales pares $(x, y)$. Esto es análogo a cómo los números complejos “extienden” los números reales y los convierten en algo con dos dimensiones (un componente real y un componente imaginario).
+
+Una extensión de campo es un concepto muy abstracto y, francamente, la relación entre un campo y su extensión no importa desde un concepto puramente funcional.
+
+Piénsalo de esta manera:
+
+
+
+Una curva elíptica en $G_2$ es una curva elíptica donde tanto el elemento $x$ como el $y$ son objetos bidimensionales.
+
+### El punto G2 en Python
+
+Basta de teoría, vamos a codificar esto y ver un punto $G_2$. Instala la biblioteca `py_ecc` de la siguiente manera.
+
+```bash
+python -m pip install py_ecc
+```
+
+Ahora, importemos las funciones que necesitamos de esta
+
+```python
+from py_ecc.bn128 import G1, G2, pairing, add, calculate, eq
+
+print(G1)
+# (1, 2)
+print(G2)
+#((10857046999023057135944570762232829481370756359578518086990519993285655852781, 11559732032986387107991004021392285783925812861821192530917403151452391805634), (8495653923123431417604973247489272438418190587263600148770280649306958101930, 4082367875863433681332203403145435568316851327593401208105741076214120093531))
+```
+
+Si miras de cerca, Verás que `G2` es un par de tuplas. La primera tupla es el punto $x$ bidimensional y la segunda tupla es el punto $y$ bidimensional.
+
+`G1` y `G2` son los puntos generadores de sus respectivos grupos.
+
+Tanto `G1` como `G2` tienen el mismo orden (número de puntos en la curva):
+
+```python
+from py_ecc.bn128 import G1, G2, eq, curve_order, calculate, eq, curve_order
+
+x = 10 # elegido aleatoriamente
+assert eq(multiply(G2, x + curve_order), calculate(G2, x))
+assert eq(multiply(G1, x + curve_order), calculate(G1, x))
+```
+
+Aunque los puntos `G2` pueden parecer un poco extraños, su comportamiento es el mismo que el de otros grupos cíclicos, especialmente el grupo `G1` con el que estamos familiarizados. Esto significa que podemos construir otros puntos con multiplicación escalar (que en realidad es una suma repetida) como se esperaba
+
+```python
+print(eq(add(G1, G1), multiplicar(G1, 2)))
+# True
+print(eq(add(G2, G2), multiplicar(G2, 2)))
+# True
+```
+
+Debería ser obvio que solo puedes agregar elementos del mismo grupo.
+
+```python
+add(G1, G2) # TypeError
+```
+
+Por cierto, esta biblioteca anula algunos operadores aritméticos (puedes hacerlo en Python), lo que significa que puedes hacer lo siguiente:
+
+```python
+print(G1 + G1 + G1 == G1*3)
+# True
+
+# Lo anterior es lo mismo que esto:
+eq(add(add(G1, G1), G1), multiplicar(G1, 3))
+# True
+```
+
+## Emparejamientos bilineales en Python
+Al principio de este artículo, dijimos que los emparejamientos bilineales se pueden usar para verificar si los logaritmos discretos de $P$ y $Q$ se multiplican para producir el logaritmo discreto de $R$, es decir, $PQ = R$.
+
+Así es como podemos hacerlo en Python:
+
+```python
+from py_ecc.bn128 import G1, G2, pairing, multiplicar, eq
+
+P = multiplicar(G1, 3)
+Q = multiplicar(G2, 8)
+
+R = multiplicar(G1, 24)
+
+assert eq(pairing(Q, R), pairing(G2, R))
+```
+
+De manera bastante molesta, la biblioteca requiere que pases el punto `G2` como primer argumento para `pairing`.
+
+### Igualdad de productos
+También al principio de este artículo dijimos que un emparejamiento puede verificarse:
+
+$$e(P_2, P_1) \stackrel{?}{=} e(Q_2, Q_1)$$
+
+Así es como podemos hacerlo en Python:
+
+```python
+from py_ecc.bn128 import G1, G2, pairing, calculate, eq
+
+P_1 = calculate(G1, 3)
+P_2 = calculate(G2, 8)
+
+Q_1 = calculate(G1, 6)
+Q_2 = calculate(G2, 4)
+
+assert eq(pairing(P_2, P_1), matching(Q_2, Q_1))
+```
+
+### El operador binario de $G_T$
+Los elementos en $G_T$ se combinan usando "multiplicación", pero tenga en cuenta que esto es en realidad una anulación sintáctica en Python:
+
+```python
+de py_ecc.bn128 import G1, G2, emparejamiento, multiplicar, eq
+
+# 2 * 3 = 6
+P_1 = multiplicar(G1, 2)
+P_2 = multiplicar(G2, 3)
+
+# 4 * 5 = 20
+Q_1 = multiplicar(G1, 4)
+Q_2 = multiplicar(G2, 5)
+
+# 10 * 12 = 120 (6 * 20 = 120 también)
+R_1 = multiplicar(G1, 13)
+R_2 = multiplicar(G2, 2)
+
+assert eq(emparejamiento(P_2, P_1) * emparejamiento(Q_2, Q_1), emparejamiento(R_2, R_1))
+
+# ¡Falla!
+```
+
+¡Pero la afirmación falla!
+
+Los elementos en $G_T$ se comportan como "potencias" de una base.
+
+Recuerde del álgebra que
+
+$$b^xb^y = b^{x+y}$$
+
+Supongamos que generamos un elemento en $G_T$ como $e(3G_2, 2G_1)$. Podríamos pensar en el elemento como $6G_T$, pero sería mucho más útil pensar en él como $b^6G_T$. No hay necesidad de saber qué es $b$ en este contexto, solo que existe.
+
+Por lo tanto, para que nuestro código anterior funcione, cambie $R_1$ y $R_2$ para multiplicarlos por 26.
+
+Nuestro código calcula efectivamente:
+
+$$
+\begin{align*}
+b ^ {2 \cdot 3} * b ^ {4 \cdot 5} = b ^ {13 \cdot 2}\\
+b ^ 6 \cdot b ^ {20} = b ^ {26}
+\end{align*}
+$$
+
+```python
+from py_ecc.bn128 import G1, G2, pairing, calculate, eq
+
+# 2 * 3 = 6
+P_1 = calculate(G1, 2)
+P_2 = calculate(G2, 3)
+
+# 4 * 5 = 20
+Q_1 = calculate(G1, 4)
+Q_2 = calculate(G2, 5)
+
+# 13 * 2 = 16
+R_1 = multiplicar(G1, 13)
+R_2 = multiplicar(G2, 2)
+
+# b ^ {2 * 3} * b ^ {4 * 5} = b ^ {13 * 2}
+# b ^ 6 * b ^ 20 = b ^ 26
+
+assert eq(pairing(P_2, P_1) * pairing(Q_2, Q_1), pairing(R_2, R_1))
+```
+
+## Emparejamientos bilineales en Ethereum
+### Especificación EIP 197
+La biblioteca py_ecc es mantenida por la [Fundación Ethereum](https://ethereum.org/), y es lo que alimenta la precompilación en la dirección 0x8 en la [implementación de PyEVM](https://github.com/ethereum/py-evm).
+
+La precompilación de Ethereum definida en [EIP-197](https://eips.ethereum.org/EIPS/eip-197) funciona en puntos en `G1` y `G2`, y *implícitamente* funciona en puntos en $G_T$.
+
+La especificación de esta precompilación parecerá un poco extraña al principio. Toma una lista de puntos G1 y G2 dispuestos de la siguiente manera:
+
+`A₁B₁A₂B₂...AₙBₙ : Aᵢ ∈ G1, Bᵢ ∈ G2`
+
+Estos se crearon originalmente como
+
+```
+A₁ = a₁G1
+B₁ = b₁G2
+A₂ = a₂G1
+B₂ = b₂G2
+...
+Aₙ = aₙG1
+Bₙ = bₙG2
+```
+
+La precompilación devuelve 1 si lo siguiente es verdadero
+
+```
+a₁b₁ + a₂b₂ + ... + aₙbₙ = 0
+```
+
+y cero en caso contrario.
+
+Al principio, esto puede resultar un poco confuso. Esto parece implicar que la precompilación toma el logaritmo discreto de cada uno de los puntos, lo que se acepta como inviable en general. Además, ¿por qué no se comporta como el emparejamiento de los ejemplos anteriores de Python? Los ejemplos anteriores devolvieron un elemento en $G_T$, pero esta precompilación devuelve un valor booleano.
+
+#### Justificación de la decisión de diseño de EIP 197
+El primer problema es que los elementos en $G_T$ son grandes, específicamente, son objetos de 12 dimensiones.
+
+Esto ocupará mucho espacio en la memoria, lo que generará mayores costos de gas. Además, debido a cómo funcionan la mayoría de los algoritmos de verificación ZK (esto está fuera del alcance de este artículo), generalmente no verificamos el valor de la salida de un emparejamiento, sino solo que sea igual a otros emparejamientos. En concreto, el paso final de [Groth16](https://www.rareskills.io/post/groth16) (el algoritmo de conocimiento cero utilizado por Tornado Cash) se parece al siguiente:
+
+$$
+e(A₁, B₂) = e(α₁, β₂) + e(L₁, γ₂) + e(C₁, δ₂)
+$$
+
+Donde cada variable es un punto de la curva elíptica de $\mathbb{G}_1$ o $\mathbb{G}_2$ según su notación de subíndice (habríamos utilizado letras griegas mayúsculas para mantener la coherencia con nuestra notación, pero se parecen demasiado al alfabeto latino).
+
+Los significados de estas variables no son importantes en esta etapa. Lo que importa es el hecho de que se puedan escribir como la suma de "productos" (emparejamiento de curvas elípticas). En concreto, podemos escribirlo como
+
+$$
+0 = e(−A₁, B₂) + e(α₁, β₂) + e(L₁, γ₂) + e(C₁, δ₂)
+$$
+
+¡Y ahora coincide perfectamente con la especificación de precompilación!
+
+No se trata solo de Groth16, la mayoría de los algoritmos zk tienen una fórmula de verificación que se parece a esa, por lo que la precompilación se diseñó para trabajar con sumas de emparejamientos en lugar de devolver el valor de un solo emparejamiento.
+
+Si miramos el código de verificación de [Tornado Cash](https://www.rareskills.io/post/how-does-tornado-cash-work), podemos ver que está implementando esto exactamente (incluso las letras griegas coinciden, pero no te preocupes si aún no lo entiendes). El $\beta_2$ simplemente significa que es un punto $\mathbb{G}_2$, $\alpha_1$ significa un punto $\mathbb{G}_1$, etc.
+
+
+
+Dentro de la función de emparejamiento es donde se realiza la llamada a `address(8)` para completar el cálculo de emparejamiento y determinar si la prueba es válida o no.
+
+*A veces, el grupo $G_T$ se denomina $G_{12}$ en el contexto de EIP 197.*
+
+#### Suma de logaritmos discretos
+La idea clave aquí es que si
+
+$$ab + cd = 0$$
+
+Entonces también debe ser cierto que
+
+$$A₁B₂ + C₁D₂ = 0₁₂ \space\space\space\space A₁,C₁ ∈ G1, B₂,D₂ ∈ G2$$
+
+en el grupo $\mathbb{G}_{12}$.
+
+La precompilación en realidad no calcula el logaritmo discreto, simplemente verifica si la suma de los pares es cero.
+
+La suma de los emparejamientos es cero si y sólo si la suma de los productos de los logaritmos discretos es cero.
+
+## Ejemplo de solidez de extremo a extremo de emparejamientos bilineales
+
+Tomemos estas entradas de `a`, `b`, `c` y `d`.
+
+```
+a = 4
+b = 3
+c = 6
+d = 2
+
+-ab + cd = 0
+```
+
+Al ponerlo en la fórmula podemos obtener
+
+$$
+A₁B₂ + C₁D₂ = e(−aG1, bG2) + e(cG1, dG2) = 0
+$$
+
+En Python esto equivaldrá a
+
+```python
+from py_ecc.bn128 import neg, multiplicar, G1, G2
+a = 4
+b = 3
+c = 6
+d = 2
+# Niega G1 * a para que la ecuación sume 0
+
+print(neg(multiply(G1, a)))
+#(3010198690406615200373504922352659861758983907867017329644089018310584441462, 17861058253836152797273815394432013122766662423622084931972383889279925210507)
+imprimir(multiplicar(G2, b))
+# ((2725019753478801796453339367788033689375851816420509565303521482350756874229, 7273165102799931111715871471550377909735733 521218303035754523677688038059653), (2512659008974376214222774206987427162027254181373325676825515531566330959255, 957874124722006818841961785324909313781880061366718538693995380805373202866))
+imprimir(multiplicar(G1, c))
+# (4503322228978077916651710446042370109107355802721800704639343137502100212473, 6132642251294427119375180147349983541569387941788025780665104001559216576968)
+imprimir(multiplicar(G2, d))
+# ((18029695676650738226693292988307914797657423701064905010927197838374790804409, 14583779054894525174450323658765874724019480979794335525732096752006891875705, (2140229616977736810657479771656733941598412 651537078903776637920509952744750, 11474861747383700316476719153975578001603231366361248090558603872215261634898))
+```
+
+Aquí está la salida en un formato estructurado
+
+```python
+aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462,
+aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507,
+
+bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229,
+bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653,
+bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255,
+bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866,
+
+cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473,
+cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968,
+
+dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409,
+dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705,
+dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750,
+dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898
+```
+
+Ahora que tenemos los valores cifrados en puntos en los grupos $\mathbb{G}_1$ y $\mathbb{G}_2$, alguien más o un programa puede confirmar que calculamos $e(A_1,B_2)+e(C_1,D_2)=0$ correctamente sin conocer los valores individuales. valores de `a`, `b`, `c` o `d`. Aquí hay un contrato de Solidity que usa la precompilación ecPairing para confirmar que calculamos las ecuaciones con valores válidos.
+
+Creamos un archivo Pairings.sol para [hacer pruebas unitarias en Foundry](https://www.rareskills.io/post/foundry-testing-solidity) (a continuación proporcionaremos el archivo de prueba)
+
+```solidity
+// SPDX-License-Identifier: MIT
+pragma solidity ^0.8.13;
+contract Pairings {
+ /**
+ * devuelve verdadero si == 0,
+ * devuelve falso si != 0,
+ * revierte con "Emparejamiento incorrecto" si el emparejamiento no es válido
+ */
+ function run(uint256[12] memory input) public view returns (bool) {
+ assembly {
+ let success := staticcall(gas(), 0x08, input, 0x0180, input, 0x20)
+ if success {
+ return(input, 0x20)
+ }
+ }
+ revert("Wrong pairing");
+ }
+}
+```
+
+Usamos este archivo de prueba de Foundry para implementar y llamar a nuestro contrato de emparejamientos para confirmar nuestro cálculo de ecPairing. El siguiente archivo lo llamamos `TestPairings.sol`.
+
+```solidity
+// SPDX-License-Identifier: MIT
+pragma solidity ^0.8.13;
+import "forge-std/Test.sol";
+import "../src/Pairings.sol";
+
+contract PairingsTest is Test {
+ Pairings public pairings;
+
+ function setUp() public {
+ pairings = new Pairings();
+ }
+
+ function testPairings() public view {
+ uint256 aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462;
+ uint256 aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507;
+
+ uint256 bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229;
+ uint256 bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653;
+ uint256 bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255;
+ uint256 bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866;
+
+ uint256 cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473;
+ uint256 cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968;
+
+ uint256 dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409;
+ uint256 dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705;
+ uint256 dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750;
+ uint256 dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898;
+
+ uint256[12] memory points = [
+ aG1_x,
+ aG1_y,
+ bG2_x2,
+ bG2_x1,
+ bG2_y2,
+ bG2_y1,
+ cG1_x,
+ cG1_y,
+ dG2_x2,
+ dG2_x1,
+ dG2_y2,
+ dG2_y1
+ ];
+
+ bool x = pairings.run(points);
+ console2.log("result:", x);
+ }
+}
+```
+
+**Tenga en cuenta que la forma en que se organizan los puntos G2 no es la misma forma en que Python presenta los puntos G2.**
+
+Esto pasa e imprime `true` en la consola. Tenga en cuenta que los puntos han sido etiquetados por su nombre de variable, a qué grupo pertenecen y si representan una `x` o una `y` del punto de la curva elíptica.
+
+Es importante tener en cuenta que la precompilación ecPairing no espera ni requiere una matriz y que nuestra elección de usar una con inline-assembly es simplemente opcional. Uno podría hacer lo mismo con solidity de la siguiente manera:
+
+```solidity
+function run(bytes calldata input) public view returns (bool) {
+ // optional, the precompile checks this too and reverts (with no error) if false, this helps narrow down possible errors
+ if (input.length % 192 != 0) revert("Points must be a multiple of 6");
+ (bool success, bytes memory data) = address(0x08).staticcall(input);
+ if (success) return abi.decode(data, (bool));
+ revert("Wrong pairing");
+}
+```
+
+Y actualice el archivo de prueba de la siguiente manera:
+
+```solidity
+function testPairings() public view {
+ uint256 aG1_x = 3010198690406615200373504922352659861758983907867017329644089018310584441462;
+ uint256 aG1_y = 17861058253836152797273815394432013122766662423622084931972383889279925210507;
+
+ uint256 bG2_x1 = 2725019753478801796453339367788033689375851816420509565303521482350756874229;
+ uint256 bG2_x2 = 7273165102799931111715871471550377909735733521218303035754523677688038059653;
+ uint256 bG2_y1 = 2512659008974376214222774206987427162027254181373325676825515531566330959255;
+ uint256 bG2_y2 = 957874124722006818841961785324909313781880061366718538693995380805373202866;
+
+ uint256 cG1_x = 4503322228978077916651710446042370109107355802721800704639343137502100212473;
+ uint256 cG1_y = 6132642251294427119375180147349983541569387941788025780665104001559216576968;
+
+ uint256 dG2_x1 = 18029695676650738226693292988307914797657423701064905010927197838374790804409;
+ uint256 dG2_x2 = 14583779054894525174450323658765874724019480979794335525732096752006891875705;
+ uint256 dG2_y1 = 2140229616977736810657479771656733941598412651537078903776637920509952744750;
+ uint256 dG2_y2 = 11474861747383700316476719153975578001603231366361248090558603872215261634898;
+
+ bytes memory points = abi.encode(
+ aG1_x,
+ aG1_y,
+ bG2_x2,
+ bG2_x1,
+ bG2_y2,
+ bG2_y1,
+ cG1_x,
+ cG1_y,
+ dG2_x2,
+ dG2_x1,
+ dG2_y2,
+ dG2_y1
+ );
+
+ bool x = pairings.run(points);
+ console2.log("result:", x);
+}
+```
+
+Esto se aprobará y devolverá verdadero al igual que la implementación inicial porque envía exactamente los mismos datos de llamada a la precompilación.
+
+La única diferencia es que en la primera implementación, el archivo de prueba envía una matriz de puntos al contrato de emparejamiento que utiliza ensamblaje en línea para cortar los primeros 32 bytes (longitud de la matriz) y envía el resto a la precompilación. Y en la segunda implementación, el archivo de prueba envía los puntos codificados con abi al contrato de emparejamiento que los reenvía tal como están a la precompilación.
+
+## Obtenga más información de RareSkills
+
+Este material se extrajo de nuestro [Curso de conocimiento cero](https://www.rareskills.io/zk-bootcamp). Consulte el programa para obtener más información.
+
+---
+
+## Realmente quiero comprender las matemáticas detrás de los emparejamientos bilineales
+
+Se le advirtió que las matemáticas son bastante complejas y comprenderlas no lo ayudará a implementar ZK Proofs, que es el objetivo de este libro. Probablemente haya utilizado SHA-256 o Keccak256 de manera productiva sin conocer sus componentes internos, y le sugerimos *enfáticamente* que trate los emparejamientos de la misma manera en esta etapa de su recorrido. Sin embargo, si nuestras advertencias no te han disuadido, aquí tienes un buen recurso si aún quieres adentrarte en el tema: [Pairings for Beginners](https://static1.squarespace.com/static/5fdbb09f31d71c1227082339/t/5ff394720493bd28278889c6/1609798774687/PairingsForBeginners.pdf). *Aquí hay dragones.*
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/elliptic-curve-addition_es.md b/spanish-es/elliptic-curve-addition_es.md
new file mode 100644
index 0000000..0f5874b
--- /dev/null
+++ b/spanish-es/elliptic-curve-addition_es.md
@@ -0,0 +1,292 @@
+# Suma de puntos de Curva Elíptica
+
+Este artículo describe cómo funciona la suma de curvas elípticas sobre números reales.
+
+La criptografía utiliza curvas elípticas sobre campos finitos, pero las curvas elípticas son más fáciles de conceptualizar en un plano cartesiano real. Este artículo está dirigido a programadores e intenta lograr un equilibrio entre ser demasiado matemático y demasiado impreciso.
+
+## Definición teórica de conjuntos de curvas elípticas
+El [conjunto](https://www.rareskills.io/post/set-theory) de puntos en una curva elíptica forma un grupo bajo la suma de puntos de curva elíptica.
+
+Con suerte, si has estado siguiendo nuestra [introducción a la teoría de grupos](rareskills.io/post/group-theory-and-coding), entonces realmente entendiste la mayor parte de esto, además de qué es la “suma de puntos”. Pero esa es la belleza del álgebra abstracta, ¿no? No necesitas saber qué es eso, y aún así entiendes la oración anterior.
+
+Las curvas elípticas son una familia de curvas que tienen la fórmula
+
+$$ y^2 = x^3 + ax + b $$
+
+Dependiendo del valor de a y b que elijas, obtendrás una curva que se parece a alguna de las siguientes:
+
+
+
+Un punto en una curva elíptica es un Par $(x, y)$ que satisface $y² = x³ + ax + b$ para $a$ y $b$ dados.
+
+Por ejemplo, el punto $(3, 6)$ está en la curva $y² = x³ + 9$ porque $6² = 3³ + 9$. En términos de teoría de grupos, $(3, 6)$ es un miembro del conjunto definido por $y² = x³ + 9$. Como estamos tratando con números reales, el conjunto tiene cardinalidad infinita.
+
+La idea aquí es que podemos tomar dos puntos de este conjunto, hacer un operador binario y obtendremos otro punto que también está en el conjunto. Es decir, es un par $(x, y)$ que también se encuentra en la curva.
+
+**En lugar de pensar en las curvas elípticas como un gráfico, piense en ellas como un conjunto infinito de puntos. Los puntos están en el conjunto si y solo si satisfacen la ecuación de la curva elíptica.**
+
+Una vez que vemos estos puntos como un conjunto, verlos como un grupo no es un misterio. Simplemente tomamos dos puntos y producimos un tercero de acuerdo con las reglas de un grupo.
+
+Específicamente, para ser un grupo, el conjunto de puntos debe tener:
+
+- un operador binario que sea cerrado y asociativo, es decir, que produzca otro punto en el conjunto
+- el conjunto debe tener un elemento de identidad $I$
+- cada punto en el conjunto debe tener un inverso tal que cuando los dos se combinen con el operador binario, el resultado sea $I$
+
+## Las curvas elípticas forman un grupo abeliano bajo la adición
+
+Aunque no sabemos cómo funciona el operador binario, sí sabemos que toma dos puntos $(x, y)$ en la curva y devuelve otro punto en la curva. Debido a que el operador es cerrado, sabemos que el punto será de hecho una solución válida para la ecuación de la curva elíptica, no un punto en otro lugar.
+
+También sabemos que este operador binario es asociativo (y conmutativo, según el encabezado de la sección).
+
+Entonces, dados tres puntos en la curva elíptica $A$, $B$ y $C$ (o $(x_a, y_a)$, $(x_b, y_b)$ y $(x_c, y_c)$ si lo prefiere), sabemos que lo siguiente es cierto:
+
+- $(A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)$
+- $A ⊕ B = B ⊕ A$
+
+Uso $⊕$ porque sabemos que este operador binario no es una suma en ningún sentido normal, sino un operador binario (de nuevo, recuerde que, según la teoría de conjuntos, un operador binario toma dos elementos de un conjunto y devuelve otro elemento de un conjunto; cómo lo hace no es central para la definición).
+
+También sabemos que tiene que haber un elemento identidad en alguna parte. Es decir, cualquier punto $(x, y)$ que caiga en la curva se combina con el elemento identidad, el resultado es el mismo punto $(x, y)$ sin cambios.
+
+Y como se trata de un grupo y no de un monoide, cada punto debe tener una inversa tal que $P ⊕ P⁻¹ = I$, donde $I$ es el elemento identidad.
+
+### El elemento identidad
+
+Intuitivamente, podríamos pensar que $(0, 0)$ o $(1, 1)$ son el elemento identidad, ya que algo así suele estar en otros grupos, pero se puede ver en los gráficos anteriores que esos puntos generalmente no se encuentran en la curva. Como no pertenecen al conjunto de puntos en $y² = x³ + ax + b$, no son parte del grupo.
+
+Pero recordemos que, según la teoría de conjuntos, podemos definir operadores binarios como queramos sobre conjuntos definidos arbitrariamente. Esto nos permite añadir un elemento especial que técnicamente no está en la curva pero que, por definición, es el elemento identidad.
+
+Me gusta pensar en el elemento identidad como "el punto que está en ninguna parte" porque si combinas la nada con cualquier punto real, nada cambia. Es molesto que los matemáticos llamen a este punto, el elemento identidad, "el punto en el infinito".
+
+Un momento, ¿no se supone que este punto satisface $y² = x³ + ax + b$? La nada (o el infinito) no es un valor válido para $(x, y)$.
+
+Ahh, pero recuerda, ¡podemos definir conjuntos como queramos! Definimos el conjunto que forma la curva elíptica como puntos en la curva elíptica y el punto de la nada.
+
+Porque los operadores binarios son solo subconjuntos de un producto cartesiano (una relación), y podemos definir la relación como queramos. Podemos tener tantas declaraciones “if” chapuceras en nuestra aritmética como queramos y aun así seguir las leyes de grupo.
+
+## La suma es cerrada.
+
+Sin pérdida de generalidad, tomemos la curva elíptica
+
+$$ y² = x³ + 10 $$
+
+Para ilustrar cómo se intersecan las líneas en las curvas elípticas, dibujemos una línea casi vertical $y = 10x$
+
+(Podría ser 1000x para hacerla más vertical, pero obtendríamos inestabilidad numérica como verás más adelante)
+
+Obtenemos el siguiente conjunto de gráficos.
+
+
+
+Resulta que, aunque parezca que la línea violeta ($y = 10x$) sube más rápido que la curva azul ($y² = x³ + 10$), siempre se cruzarán.
+
+Si nos alejamos lo suficiente, podemos ver la intersección. Esto es cierto en general.
+
+**Siempre que x no sea "perfectamente vertical", si cruza dos puntos de la curva, siempre cruzará un tercero.** Dos de esos puntos podrían ser el mismo punto si uno de los puntos de intersección es un punto tangente.
+
+El "si intersectamos dos puntos" es importante. Si desplazamos nuestra línea violeta hacia la izquierda para que no cruce el "giro en U" de la curva elíptica, entonces sólo se cruzará en un punto
+
+Otra forma de entenderlo:
+
+**Si una línea recta cruza una curva elíptica exactamente en dos puntos, y ninguno de los puntos de intersección son intersecciones tangentes, entonces debe ser perfectamente vertical.**
+
+Podrías elaborar una prueba algebraica a partir de las fórmulas anteriores, pero creo que el argumento geométrico es más intuitivo.
+
+Te recomiendo que te detengas aquí y dibujes algunas curvas y líneas elípticas y te convenzas de esto visualmente.
+
+Nuestra excepción para las líneas verticales en realidad hace que los elementos inversos e identidades encajen perfectamente.
+
+**La inversa de un punto de una curva elíptica es el negativo del valor y del par.** Es decir, la inversa de $(x, y)$ es $(x, -y)$ y viceversa. Dibujar una línea a través de dichos puntos crea una línea perfectamente vertical.
+
+El elemento de identidad es el "punto en el infinito" al que aludimos antes, es simplemente el punto "allá arriba" cuando dibujamos una línea vertical.
+
+### Grupo abeliano
+
+El hecho de que los puntos de la curva elíptica sean un grupo bajo nuestro principio "2 puntos siempre dan como resultado un tercero excepto por la identidad" hace que su naturaleza conmutativa sea obvia.
+
+Cuando elegimos dos puntos, solo hay otro tercer punto. No se pueden obtener cuatro intersecciones en una curva elíptica. Como solo tenemos una solución posible, entonces está claro que $A ⊕ B = B ⊕ A$.
+
+## Por qué la suma de curvas elípticas invierte el eje x
+
+Pasamos por alto un detalle muy importante en la última sección, porque realmente merece una sección propia.
+
+En su forma actual, tiene un error si agregamos dos puntos donde la intersección ocurre en el medio.
+
+
+
+Usando nuestras definiciones anteriores, lo siguiente debe ser verdadero
+
+$$
+\begin{align*}
+A ⊕ B &= C \\
+A ⊕ C &= B \\
+B ⊕ C &= A
+\end{align*}
+$$
+
+Con un poco de álgebra, derivaremos una contradicción
+
+$$
+\begin{align*}
+(B ⊕ C) ⊕ B &= C \\
+B ⊕ C &= \mathsf{inv}(B) ⊕ C \\
+B &= \mathsf{inv}(B)
+\end{align*}
+$$
+
+Esto dice que $B$ es igual a su inverso. Pero $B$ no es el elemento identidad (que es el único elemento que puede ser el inverso de sí mismo), por lo que tenemos una contradicción.
+
+Afortunadamente, hay una manera de solucionar esto. Simplemente defina la suma de puntos como el tercer punto *volteado sobre el eje y*. Nuevamente, se nos *permite hacer esto* porque los operadores binarios se pueden definir como queramos, solo nos preocupamos de que nuestras definiciones satisfagan las leyes de grupo.
+
+A continuación se muestra gráficamente la forma correcta de sumar puntos de una curva elíptica
+
+
+
+## Fórmula para la suma
+
+Usando algo de álgebra y dados dos puntos
+
+$$
+\begin{align*}
+P₁ &= (x₁, y₁) \\
+P₂ &= (x₂, y₂)
+\end{align*}
+$$
+
+Se puede obtener la forma de calcular $P₃ = (x₃, y₃)$ donde $P₃ = P₁ ⊕ P₂$ usando la siguiente fórmula.
+
+$$
+\begin{align*}
+\lambda &= \frac{y₂ - y₁}{x₂ - x₁} \\
+x₃ &= \lambda² - x₁ - x₂ \\
+y₃ &= \lambda(x₃ - x₁) - y₁
+\end{align*}
+$$
+
+### Demostración algebraica de conmutatividad y asociatividad
+
+Como tenemos una ecuación en forma cerrada, podemos demostrar algebraicamente que $T⊕U = U⊕T$ dados los puntos $T$ y $U$.
+
+Lo hacemos de la siguiente manera:
+
+$$\begin{align*}
+P &= T ⊕ U \\
+Q &= U ⊕ T \\
+P &= Q
+\end{align*}$$
+
+```python
+var('y_t', 'y_u', 'x_t', 'x_u')
+lambda_p = (y_u - y_t)/(x_u - x_t)
+x_p = lambda_p^2 - x_t - x_u
+y_p = (lambda_p*(x_t - x_p) - y_t)
+
+lambda_q = (y_t - y_u)/(x_t - x_u)
+x_q = lambda_q^2 - x_u - x_t
+y_q = (lambda_q*(x_u - x_q) - y_u)
+```
+
+Aquí hay una captura de pantalla de la ejecución del código anterior en Jupyter Notebook y la impresión del resultado. El sistema de álgebra computacional necesita un poco de persuasión, pero podemos ver claramente `x_q == x_p` y `y_q == y_p`.
+
+
+
+$P = Q$ para todos los valores de $(x_t, y_t)$ y $(x_u, y_u)$. Obtenemos un error de división por cero si $x_t = x_u$, pero esto significa que son el mismo punto y eso es obviamente conmutativo.
+
+Podemos utilizar técnicas similares para demostrar la asociatividad, pero desafortunadamente esto es extremadamente complicado, por lo que remitimos al lector interesado a otra [prueba de asociatividad](https://www.scirp.org/journal/paperinformation.aspx).
+
+## Las curvas elípticas cumplen con la propiedad de grupo abeliano
+
+Veamos que las curvas elípticas cumplen con la propiedad de grupo.
+
+1. El operador binario es cerrado. Se interseca con un tercer punto en la curva o con el punto en el infinito (identidad). Tenemos la garantía de obtener un tercer punto válido cuando intersecamos dos puntos. El operador binario es asociativo.
+2. El grupo tiene un elemento identidad.
+3. Cada punto tiene un inverso.
+4. El grupo es abeliano porque A ⊕ B = B ⊕ A
+
+Un operador binario debe aceptar todos los pares posibles del conjunto. ¿Qué sucede si el par es el mismo elemento, es decir, A ⊕ A?
+
+## Multiplicación de puntos: sumando un punto consigo mismo
+
+Pensemos en esto en términos límite. Sumar un punto consigo mismo es como acercar dos puntos infinitesimalmente hasta que se convierten en el mismo punto. Cuando ocurre esta convergencia, la pendiente de la línea será tangente a la curva.
+
+Por lo tanto, sumar un punto consigo mismo es simplemente tomar la derivada en ese punto, obtener la intersección y luego invertir el eje $y$.
+
+La siguiente imagen demuestra gráficamente $A ⊕ A = 2A$.
+
+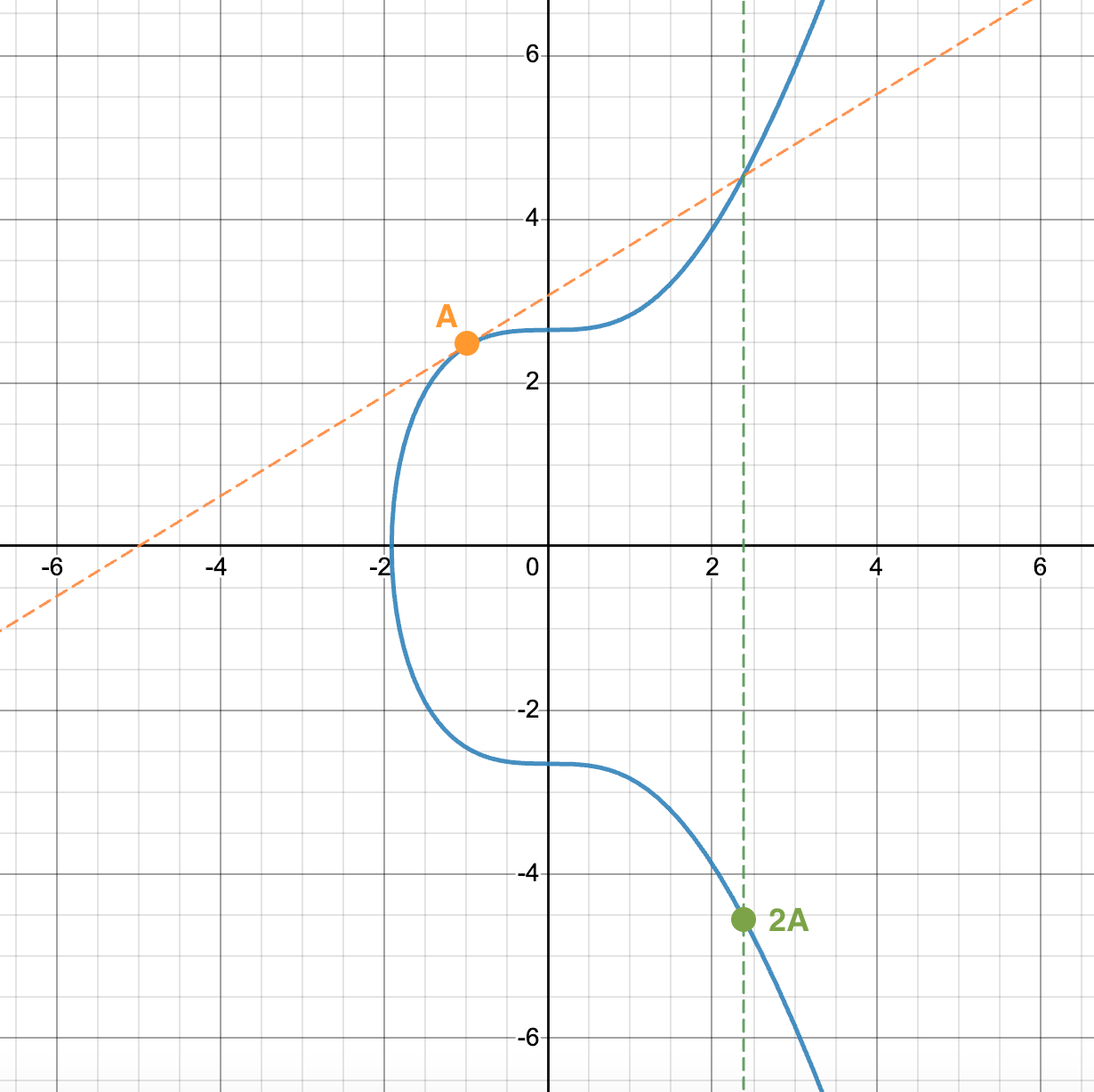
+
+### Atajo para la multiplicación de puntos
+
+¿Qué sucede si queremos calcular $1000A$ en lugar de $2A$? Parecería que se trata de una operación $\mathcal{O}(n)$, pero no lo es.
+
+Debido a la asociatividad, podemos escribir $1000A$ como
+
+$$1000A = 512A ⊕ 256A ⊕ 128A ⊕ 64A ⊕ 32A ⊕ 8A$$
+
+$512A$ (y los otros términos) se pueden calcular rápidamente porque 512 es simplemente $A$ duplicado 9 veces.
+
+Por lo tanto, en lugar de hacer 1000 operaciones, podemos hacerlo en 14 (9 para calcular 512, almacenar en caché los resultados intermedios y luego 5 sumas).
+
+En realidad, esta es una propiedad importante cuando llegamos a la criptografía:
+
+*Podemos multiplicar eficientemente un punto de una curva elíptica por un entero grande de manera eficiente.*
+
+## Detalles de implementación de la suma
+
+No es demasiado difícil derivar la fórmula para la suma de puntos usando álgebra simple. Cuando intersectamos dos puntos, conocemos la pendiente y los puntos por los que pasa, por lo que podemos calcular el punto de intersección.
+
+Prefiero no hacerlo aquí porque no quiero perderme en un montón de manipulaciones simbólicas.
+
+El poder de la teoría de grupos es que no nos importa cómo se ve esa manipulación simbólica. Sabemos que si hacemos nuestro operador binario en dos puntos, obtendremos otro punto en nuestro conjunto, y nuestro conjunto sigue las leyes del grupo.
+
+Si lo piensas de esa manera, las curvas elípticas son mucho más fáciles de entender.
+
+En lugar de intentar comprender las curvas elípticas de manera aislada desde cero, estudiamos un montón de otros grupos algebraicos y luego transferimos ese conocimiento e intuición a las curvas elípticas.
+
+Los números racionales bajo la suma son un grupo. Los números enteros módulo primo son un grupo bajo la multiplicación. Las matrices de determinante distinto de cero bajo la multiplicación son un grupo.
+
+Si se realiza el operador binario, se obtiene otro elemento en el conjunto. El grupo tiene un elemento identidad y cada elemento tiene un inverso. Se cumple la ley asociativa. Con todo eso en mente, no debería importarle lo que el operador ⊕ esté haciendo detrás de escena.
+
+En mi opinión, si intentas entender las matemáticas de las curvas elípticas de forma aislada de los principios básicos de la teoría de grupos, lo estás haciendo de la manera difícil. Es mucho más fácil entenderlas en el contexto de sus parientes.
+
+Eso hace que la experiencia de aprendizaje sea más fluida.
+
+### La manipulación algebraica es en realidad solo una suma asociativa.
+
+Sea $P$ un punto de la curva elíptica. ¿Qué sucede si hacemos algo como esto?
+
+$$(a + b)P + cP = aP + (a + c)P$$
+
+Al principio, puede parecer extraño que podamos hacer eso, porque si tratamos de visualizar lo que está sucediendo con la curva elíptica, seguramente nos perderemos.
+
+Recuerda, lo que parece una multiplicación es en realidad un punto que se suma consigo mismo repetidamente, así que esto es lo que sucede en realidad cuando lo miramos como un grupo
+
+$$\underbrace{(a + b)P + cP}_{((a + b + c)P)} = \underbrace{aP + (b + c)P}_{(a + b + c)P}$$
+
+$$
+\begin{align*}
+(a + b + c)P &= (a + b + c)P \\
+(aP + bP) + cP &= aP + (bP + cP) \\
+(a + b)P + cP& = aP (b + c)P
+\end{align*}
+$$
+
+La "multiplicación" escalar no es "distributiva" en el sentido en que pensaríamos en el álgebra normal. Es solo una forma abreviada de reorganizar el orden en el que sumamos P a sí mismo.
+
+En realidad, simplemente sumamos $P$ a sí mismo $(a + b + c)$ veces. El orden en que lo hacemos no importa debido a la asociatividad.
+
+Por lo tanto, cuando se ve una manipulación como esa, nuestro grupo no obtuvo de repente un operador binario de multiplicación, es solo una abreviatura engañosa.
+
+## Curvas elípticas en cuerpos finitos
+
+Si hiciéramos curvas elípticas sobre números reales para una aplicación real, serían muy inestables numéricamente porque el punto de intersección podría requerir muchos decimales para calcularse.
+
+En realidad, todo lo hacemos con [aritmética modular](https://www.rareskills.io/post/finite-fields).
+
+Pero no perdemos nada de la intuición que hemos adquirido anteriormente al hacer esto.
+
+## Obtenga más información con RareSkills
+
+Este material es de nuestro curso de conocimiento cero, consulte allí para obtener más información.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
\ No newline at end of file
diff --git a/spanish-es/elliptic-curve-qap_es.md b/spanish-es/elliptic-curve-qap_es.md
new file mode 100644
index 0000000..d528e44
--- /dev/null
+++ b/spanish-es/elliptic-curve-qap_es.md
@@ -0,0 +1,258 @@
+# Evaluación de un programa aritmético cuadrático en una configuración confiable
+
+La evaluación de un [Programa Aritmético Cuadrático (QAP)](https://www.rareskills.io/post/quadratic-arithmetic-programs) en una configuración confiable permite al probador demostrar que se satisface un QAP sin revelar el testigo mientras se utiliza una prueba de tamaño constante.
+
+Específicamente, los polinomios QAP se evalúan en un punto desconocido $\tau$. La ecuación QAP
+
+$$\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) = \sum_{i=1}^m a_iw_i(x) + h(x)t(x)$$
+
+estará balanceada si el vector $\mathbf{a}$ satisface la ecuación y desbalanceada con una probabilidad abrumadora en caso contrario.
+
+El esquema que se muestra aquí no es un ZK Proof segura, pero es un paso adelante para mostrar cómo funciona Groth16.
+
+## Un ejemplo concreto
+
+Para hacerlo un poco menos abstracto, digamos que las matrices del [Sistema de restricciones de Rango 1 (R1CS)](https://www.rareskills.io/post/rank-1-constraint-system) $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$ tienen 3 filas y 4 columnas.
+
+$$\mathbf{L}\mathbf{a} \circ \mathbf{R}\mathbf{a} = \mathbf{O}\mathbf{a}$$
+
+Como tenemos 3 filas, significa que nuestros polinomios de interpolación serán de grado 2. Como tenemos 4 columnas, cada matriz dará como resultado 4 polinomios (para un total de 12 polinomios).
+
+Nuestro QAP será
+
+$$\sum_{i=1}^4a_iu_i(x)\sum_{i=1}^4a_iv_i(x) = \sum_{i=1}^4a_iw_i(x) + h(x)t(x)$$
+
+## Notación y preliminares
+
+Nos referimos a los puntos de la curva elíptica generadora en los grupos $\mathbb{G}_1$ y $\mathbb{G}_2$ como $G_1$ y $G_2$ respectivamente. Un elemento en $\mathbb{G}_1$ se denota como $[X]_1$. Un elemento en $\mathbb{G}_2$ se denota como $[X]_2$. Cuando puede haber ambigüedad con los subíndices que hacen referencia a los índices en una lista, decimos $X \in \mathbb{G}_1$ o $X \in \mathbb{G}_2$. Un [emparejamiento de curva elíptica](https://www.rareskills.io/post/bilinear-pairing) entre dos puntos se denota como $[X]_1 \bullet [Y]_2$.
+
+Sea $\mathbf{L}_{(*,j)}$ la $j$-ésima columna de $\mathbf{L}$. En nuestro ejemplo, las filas serán $(1,2,3)$ y las columnas $(1,2,3,4)$. Sea $\mathcal{L}(\mathbf{L}_{(*,j)})$ el polinomio obtenido al ejecutar la interpolación de Lagrange en la $j$-ésima columna de $\mathbf{L}$ utilizando los valores $x$ $(1,2,3)$ y los valores $y$ siendo los valores de la $j$-ésima columna.
+
+Como tenemos 4 columnas, obtenemos cuatro polinomios de $\mathbf{L}$
+
+$$
+\begin{align*} u_1(x) = \mathcal{L}(\mathbf{L}_{(*,1)}) =u_{12}x^2 + u_{11}x+u_{10}\\ u_2(x) = \mathcal{L}(\mathbf{L}_{(*,2)}) _{22}x^2 + u_{21}x+u_{20}\\ u_3(x) = \mathcal{L}(\mathbf{L}_{(*,3)}) =u_{32}x^2 + u_{31}x+u_{30}\\ u_4(x) = \mathcal{L}(\mathbf{L}_{(*,4)}) =u_{42}x^2 + u_{41}x+u_{40}\\
+\end{align*}
+$$
+
+cuatro polinomios de $\mathbf{R}$
+
+$$
+\begin{align*}
+v_1(x) = \mathcal{L}(\mathbf{R}_{(*,1)}) =v_{12}x^2 + v_{11}x+v_{10}\\
+v_2(x) = \mathcal{L}(\mathbf{R}_{(*,2)}) =v_{22}x^2 + v_{21}x+v_{20}\\
+v_3(x) = \mathcal{L}(\mathbf{R}_{(*,3)}) =v_{32}x^2 + v_{31}x+v_{30}\\
+v_4(x) = \mathcal{L}(\mathbf{R}_{(*,4)}) =v_{42}x^2 + v_{41}x+v_{40}\\
+\end{align*}
+$$
+
+y cuatro polinomios de $\mathbf{O}$
+
+$$
+\begin{align*}
+v_1(x) = \mathcal{L}(\mathbf{O}_{(*,1)}) =v_{12}x^2 v_{11}x+v_{10}\\
+v_2(x) = \mathcal{L}(\mathbf{O}_{(*,2)}) =v_{22}x^2 + v_{21}x+v_{20}\\
+v_3(x) = \mathcal{L}(\mathbf{O}_{(*,3)}) =v_{32}x^2 + v_{31}x+v_{30}\\
+v_4(x) = \mathcal{L}(\mathbf{O}_{(*,4)}) =v_{42}x^2 + v_{41}x+v_{40}\\
+\end{align*}
+$$
+
+Un polinomio $p_{ij}$ significa el polinomio $i$-ésimo de la potencia y el coeficiente $j$-ésimo (potencia). Por ejemplo, $j=2$ significa el coeficiente asociado con $x^2$.
+
+El QAP para nuestro ejemplo es
+
+$$
+\sum_{i=1}^4a_iu_i(x)\sum_{i=1}^4a_iv_i(x) = \sum_{i=1}^4a_iw_i(x) + h(x)t(x)
+$$
+
+donde $t(x) = (x - 1)(x - 2)(x - 3)$ y $h(x)$ es
+
+$$
+h(x)=\frac{\sum_{i=1}^4a_iu_i(x)\sum_{i=1}^4a_iv_i(x) - \sum_{i=1}^4a_iw_i(x)}{t(x)}
+$$
+
+### Los grados de los polinomios en el QAP con respecto al tamaño del R1CS
+
+Un par de observaciones sobre los grados de los polinomios en el caso general:
+
+- El grado de $u(x)$ y $v(x)$ podrían ser tan altos como $n - 1$ porque interpolan $n$ puntos, donde $n$ es el número de filas en el R1CS.
+- El grado de $w(x)$ podría ser tan bajo como 0 si la suma de los polinomios $\sum_{i=0}^m a_iw_i(x)$ suma el polinomio cero, es decir, los coeficientes se cancelan entre sí de manera aditiva.
+- $t(x)$ es de grado $n$ por definición.
+- La multiplicación de polinomios suma sus grados y la división de polinomios resta sus grados.
+
+Por lo tanto, h(x) será como máximo $n - 2$ porque
+
+$$
+\underbrace{n - 1}_{
+\deg{u(x)}} + \underbrace{n - 1}_{\deg{v(x)}} - \underbrace{n}_{\deg{t(x)}} = n - 2
+$$
+
+## Ampliando los términos
+
+Si ampliamos las sumas de nuestro ejemplo anterior, obtenemos lo siguiente
+
+$$
+\begin{align*}
+\sum_{i=1}^4 a_iu_i(x) &= a_1(u_{12}x^2 + u_{11}x+u_{10}) + a_2(u_{22}x^2 + u_{21}x+u_{20}) + a_3(u_{32}x^2 + u_{31}x+u_{30}) + a_4(u_{42}x^2 + u_{41}x+u_{40})\\
+&= (a_1u_{12}+a_2u_{22}+a_3u_{32}+a_4u_{42})x^2 + (a_1u_{11}+a_2u_{21}+a_3u_{31}+a_4u_{41})x + (a_1u_{10}+a_2u_{20}+a_3u_{30}+a_4u_{40})\\
+&=u_{2a}x^2+u_{1a}x+u_{0a}\\
+\sum_{i=1}^4 a_iv_i(x) &= a_1(v_{12}x^2 + v_{11}x+v_{10}) + a_2(v_{22}x^2 + v_{21}x+v_{20}) + a_3(v_{32}x^2 + v_{31}x+v_{30}) + a_4(v_{42}x^2 + v_{41}x+v_{40})\\
+&= (a_1v_{12}+a_2v_{22}+a_3v_{32}+a_4v_{42})x^2 + (a_1v_{11}+a_2v_{21}+a_3v_{31}+a_4v_{41})x + (a_1v_{10}+a_2v_{20}+a_3v_{30}+a_4v_{40})\\
+&=v_{2a}x^2+v_{1a}x+v_{0a}\\
+\sum_{i=1}^4 a_iw_i(x) &= a_1(w_{12}x^2 + w_{11}x+w_{10}) + a_2(w_{22}x^2 + w_{21}x+w_{20}) + a_3(w_{32}x^2 + w_{31}x+w_{30}) + a_4(w_{42}x^2 + w_{41}x+w_{40})\\
+&= (a_1w_{12}+a_2w_{22}+a_3w_{32}+a_4w_{42})x^2 + (a_1w_{11}+a_2w_{21}+a_3w_{31}+a_4w_{41})x + (a_1w_{10}+a_2w_{20}+a_3w_{30}+a_4w_{40})\\
+&=w_{2a}x^2+w_{1a}x+w_{0a}\\
+\end{align*}
+$$
+
+En cada uno de los casos, dado que estamos sumando 4 polinomios de grado 2, obtenemos un polinomio de grado 2.
+
+En la expresión general $\sum_{i=1}^m a_ip_i(x)$ produce un polinomio con, como máximo, la misma potencia que $p(x)$ (podría ser menor, si, por ejemplo, $(a_1w_{12}+a_2w_{22}+a_3w_{32}+a_4w_{42})x^2$ se suman a 0). Para mayor comodidad, hemos introducido los coeficientes $p_{ia}$, donde $i$ es la potencia del coeficiente y $_a$ significa que combinamos los polinomios con el testigo $\mathbf{a}$.
+
+Estos son los polinomios después de reducirlos de esta manera:
+
+$$
+\begin{align*}
+\sum_{i=1}^4 a_iu_i(x) &= u_{2a}x^2+u_{1a}+u_{0a}\\
+\sum_{i=1}^4 a_iv_i(x) &= v_{2a}x^2+v_{1a}+v_{0a}\\
+\sum_{i=1}^4 a_iw_i(x) &= w_{2a}x^2+w_{1a}+w_{0a}\\
+\end{align*}
+$$
+
+## Combinación de una configuración confiable con un QAP
+
+Ahora podemos aplicar la cadena de referencia estructurada de la configuración confiable para evaluar los polinomios.
+
+Es decir, dada una cadena de referencia estructurada
+
+$$
+[\Omega_2, \Omega_1, G_1], [\Theta_2, \Theta_1, G_2], \space\Omega_i \in \mathbb{G}_1, \space\Theta_i \in \mathbb{G}_2
+$$
+
+que se calculó en la configuración confiable como:
+
+$$
+\begin{align*}
+[\Omega_2, \Omega_1, G_1] &= [\tau^2G_1, \tau G_1, G_1], \space\Omega_i \in \mathbb{G}_1\\
+[\Theta_2, \Theta_1, G_1] &= [\tau^2G_2, \tau G_2, G_2], \space\Theta_i \in \mathbb{G}_2
+\end{align*}
+$$
+
+Podemos calcular
+
+$$
+\begin{align*}
+[A]_1 &=\sum_{i=1}^4 a_iu_i(\tau) = \langle[u_{2a}, u_{1a}, u_{0a}],[\Omega_2, \Omega_1, G_1]\rangle\\
+[B]_2 &=\sum_{i=1}^4 a_iv_i(\tau) = \langle[v_{2a}, v_{1a}, v_{0a}],[\Theta_2, \Theta_1, G_2]\rangle\\
+[C]_1 &=\sum_{i=1}^4 a_iw_i(\tau) = \langle[v_{2a}, v_{1a}, v_{0a}],[\Omega_2, \Omega_1, G_1]\rangle \\ \end{align*}
+$$
+
+Aquí, $u_i(\tau), v_i(\tau), w_i(\tau)$ significa que los polinomios se evaluaron utilizando la cadena de referencia estructurada generada a partir de $\tau$ en la configuración confiable, no significa "conectar $\tau$ y evaluar los polinomios". Dado que $\tau$ se destruyó después de la configuración confiable, el valor $\tau$ es desconocido.
+
+Hemos calculado la mayor parte del QAP usando la srs, pero aún no hemos calculado $h(x)t(x)$:
+
+$$
+\underbrace{\sum_{i=1}^m a_iu_i(x)}_{[A]_1}\underbrace{\sum_{i=1}^m a_iv_i(x)}_{[B]_2} = \underbrace{\sum_{i=1}^m a_iw_i(x)}_{[C]_1} + \underbrace{h(x)t(x)}_{??}
+$$
+
+## Cálculo de $h(x)t(x)$
+
+Recuerde que el grado de $t(x)$ es 3 (generalmente $n$) y el grado de $h(x)$ es 1 (generalmente $n - 2$). Si multiplicamos estos valores, podríamos obtener un polinomio de grado 3, que es más de lo que proporciona la ceremonia de potencias de tau. En cambio, las potencias de la ceremonia de tau deben ajustarse para proporcionar una cadena de referencia estructurada para $h(x)t(x)$.
+
+La persona que realiza la configuración confiable sabe que $t(x)$ es simplemente $(x - 1)(x - 2)...(x - n)$. Sin embargo, $h(x)$ es un polinomio calculado por el demostrador y modificado en función de los valores de $\mathbf{a}$, por lo que no se puede conocer durante la configuración confiable.
+
+Tenga en cuenta que no podemos evaluar $h(\tau)$ y $t(\tau)$ por separado (usando una cadena de referencia estructurada) y luego emparejarlos. Eso no daría como resultado un elemento $\mathbb{G}_1$ que necesitamos.
+
+### SRS para productos polinómicos
+
+Observe que los siguientes cálculos dan como resultado el mismo valor:
+
+- El polinomio $h(x)t(x)$ evaluado en $u$, o $(h(x)t(x))(u)$
+- $h(u)$ multiplicado por $t(u)$, o $h(u)t(u)$ ($h$ evaluado en $u$ y $t$ evaluado en $u$)
+- $h(x)$ multiplicado por la evaluación $t(u)$, luego evaluado en $u$, es decir, $(h(x)t(u))(u)$
+
+Usaremos el tercer método para calcular $h(\tau)t(\tau)$. Supongamos, sin pérdida de generalidad, que $h(x)$ es $3x^2 + 6x + 2$ y $t(u) = 4$. El cálculo sería:
+
+$$h(x)t(u) = (3x^2 + 6x + 2) \cdot 4 = 12x^2 + 24x + 8$$
+
+Si sustituimos $u$ en $12x^2 + 24x + 8$, quedaría $h(u)t(u)$.
+
+Sin embargo, evaluar este polinomio en $\tau$ requeriría que el probador conociera $\tau$. La idea clave aquí es que el cálculo anterior se puede estructurar como:
+
+$$
+h(u)t(u) = \langle[3, 6, 2], [4u^2, 4u, 4]\rangle=12u^2+24u+8
+$$
+
+Si la configuración confiable proporciona $[4u^2, 4u, 4]$, y el probador proporciona $[3, 6, 2]$, entonces el probador puede calcular $h(u)t(u)$ sin conocer $u$, porque cualquier cosa que involucre a $u$ está en el vector correcto del producto interno.
+
+### Cadena de referencia estructurada para $h(\tau)t(\tau)$
+
+Para crear una cadena de referencia estructurada para $h(\tau)t(\tau)$, creamos $n - 1$ evaluaciones de $t(\tau)$ multiplicadas por potencias sucesivas de $\tau$.
+
+$$
+[\Upsilon_{n-2}, \Upsilon_{n-3}, ..., \Upsilon_1, \Upsilon_0] = [\tau^{n-2}t(\tau)G_1, \tau^{n-3}t(\tau)G_1, ..., \tau t(\tau)G_1, t(\tau)G_1]
+$$
+
+(De manera un tanto confusa, un polinomio de grado $k$ tiene $k+1$ términos, por lo tanto, generamos $k - 1$ evaluaciones para un polinomio de grado $k - 2$. Nótese que Upsilon comienza en ${n-1}$ y termina en 0).
+
+Aquí, $n$ es el número de filas en el R1CS, y establecimos que $h$ no puede tener un grado mayor que $n - 2$.
+
+Para utilizar la cadena de referencia estructurada para calcular $h(\tau)t(\tau)$, el probador hace lo siguiente:
+
+$$h(\tau)t(\tau) = \langle[h_{n-2}, h_{n-3}, ..., h_1, h_0], [\Upsilon_{n-2}, \Upsilon_{n-3}, ..., \Upsilon_1, \Upsilon_0] \rangle$$
+
+## Evaluación de un QAP en una configuración confiable
+
+Ahora unimos todo. Supongamos que tenemos un R1CS con matrices de $n$ filas y $m$ columnas. A partir de esto, podemos aplicar la interpolación de Lagrange para convertirlo en un QAP
+
+$$\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) = \sum_{i=1}^m a_iw_i(x) + h(x)t(x)$$
+
+Los términos de suma producirán cada uno un polinomio de grado $n - 1$ (un polinomio de Lagrange tiene un grado menos que la cantidad de puntos que interpola), y el polinomio $h(x)$ tendrá un grado como máximo $n - 2$, y $t(x)$ tendrá un grado $n$.
+
+Una configuración confiable genera un elemento de campo aleatorio $\tau$ y calcula:
+
+$$
+\begin{align*}
+[\Omega_{n-1},\Omega_{n-2},..., \Omega_1, G_1] &= [\tau^{n-1}G_1, \tau^{n-2}G_1,\..., \tau G_1, G_1]\\
+[\Theta_{n-1}, \Theta_{n-2}, ..., \Theta_1, G_2] &= [\tau^{n-1}G_2, \tau^{n-2}G_2,\..., \tau G_2, G_2]\\
+[\Upsilon_{n-2}, \Upsilon_{n-3}, ..., \Upsilon_1, \Upsilon_0] &= [\tau^{n-2}t(\tau)G_1, \tau^{n-3}t(\tau)G_1, ..., \tau t(\tau)G_1, t(\tau)G_1]
+\end{align*}
+$$
+
+Tenga en cuenta que las cadenas de referencia estructuradas deben tener términos suficientes para acomodar los polinomios en el QAP.
+
+Luego, la configuración confiable destruye $\tau$ y publica las cadenas de referencia estructuradas:
+
+$$([\Omega_2, \Omega_1, G_1], [\Theta_2, \Theta_1, G_2], [\Upsilon_{n-2}, \Upsilon_{n-3}, ..., \Upsilon_1, \Upsilon_0])$$
+
+El probador evalúa los componentes del QAP de la siguiente manera:
+
+$$\underbrace{\sum_{i=1}^m a_iu_i(x)}_{A}\underbrace{\sum_{i=1}^m a_iv_i(x)}_B = \underbrace{\sum_{i=1}^m a_iw_i(x) + h(x)t(x)}_{C}$$
+
+$$
+\begin{align*}
+[A]_1 &=\sum_{i=1}^m a_iu_i(\tau) = \langle[u_{{n-1}a}, u_{{n-2}a}, \..., u_{1a}, u_{0a}],[\Omega_{n-1}, \Omega_{n-2}, \..., \Omega_1, G_1]\rangle\\
+[B]_2 &=\sum_{i=1}^m a_iv_i(\tau) = \langle[v_{{n-1}a}, v_{{n-2}a}, \..., v_{1a}, v_{0a}],[\Theta_{n-1}, \Theta_{n-2}, \..., \Theta_1, G_2]\rangle\\
+[C]_1 &=\sum_{i=0}^m a_iw_i(\tau) + h(\tau)t(\tau) = \langle[w_{{n-1}a}, w_{{n-2}a}, \..., w_{1a}, w_{0a}],[\Omega_{n-1}, \Omega_{n-2}, \..., \Omega_1, G_1]\rangle \\
+&+\langle[h_{n-2}, h_{n-3}, \..., h_1, h_0], [\Upsilon_{n-2}, \Upsilon_{n-3}, \..., \Upsilon_1, \Upsilon_0] \rangle\\
+\end{align*}
+$$
+
+El probador publica $([A]_1, [B]_2, [C]_1)$ y el verificador puede comprobar que
+
+$$[A]_1 \bullet [B]_2 \stackrel{?}= [C]_1 \bala G_2$$
+
+Si el testigo $\mathbf{a}$ satisface el QAP, entonces la ecuación anterior estará balanceada. Pero el hecho de que la ecuación esté balanceada no garantiza que el probador conozca un $\mathbf{a}$ satisfactorio porque el probador puede publicar puntos de curva elíptica arbitrarios y el verificador no sabe si en realidad se derivan del QAP.
+
+## La prueba es muy pequeña
+
+Observe que la prueba solo consta de tres puntos de curva elíptica. Si un elemento $\mathbb{G}_1$ tiene 64 bytes de tamaño y un elemento $\mathbb{G}_2$ tiene 128 bytes de tamaño, entonces la prueba tiene solo 256 bytes. ¡Esto es cierto *sin importar* el tamaño del R1CS!
+
+Cuanto más grande sea el R1CS, más trabajo tiene el probador, pero el trabajo del verificador permanece constante.
+
+La solución a este problema se describe en el siguiente capítulo sobre el [protocolo Groth16](https://www.rareskills.io/post/groth16).
+
+La prueba sigue teniendo un tamaño constante en Groth16, como se puede ver en el código fuente de Tornado Cash en la [estructura](https://github.com/tornadocash/tornado-core/blob/master/contracts/Verifier.sol#L167-L171)
+denominada `Prueba`.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/finite-fields_es.md b/spanish-es/finite-fields_es.md
new file mode 100644
index 0000000..d221219
--- /dev/null
+++ b/spanish-es/finite-fields_es.md
@@ -0,0 +1,754 @@
+# Cuerpos finitos y aritmética modular para ZK Proofs
+
+*Este artículo es el tercero de una serie. Presentamos cuerpos finitos en el contexto de circuitos para pruebas de conocimiento cero. Los capítulos anteriores son [P vs NP y su aplicación a pruebas de conocimiento cero](https://www.rareskills.io/post/p-vs-np) y [Circuitos aritméticos](https://www.rareskills.io/post/arithmetic-circuit).*
+
+En el capítulo anterior sobre circuitos aritméticos, señalamos una limitación: no podemos codificar el número $2/3$ porque no se puede representar con precisión usando binario. También señalamos que no teníamos una forma explícita de manejar el desbordamiento.
+
+Ambos problemas se pueden solucionar sin problemas con una variante de la aritmética, popular en la criptografía general, llamada *campos finitos*.
+
+## Campos finitos
+
+Dado un número primo `p`, podemos crear un campo finito con `p` elementos tomando el conjunto de números enteros $\set{0, 1, 2, …, p-1}$ y definiendo que la suma y la multiplicación se realicen módulo $p$. Comenzaremos limitándonos a los campos donde el número de elementos es primo.
+
+Por ejemplo, si el número primo $p$ es $7$, entonces los elementos en el campo finito son $\set{0, 1, 2, 3, 4, 5, 6}$. Cualquier número fuera de este rango ($≥ p$ o $< 0$) siempre se asigna a un número "equivalente" en este rango usando módulo. La palabra técnica para "equivalente" es *congruente*.
+
+El módulo calcula el resto de la división del número por el número primo. Por ejemplo, si nuestro módulo es 7, el número 12 es *congruente* con 5, es decir, $12 \pmod 7 = 5$, y el número 14 es congruente con 0. De manera similar, cuando sumamos dos números, digamos 3 + 5, la suma resultante de 8 es congruente con 1 (8 mod 7 = 1). La siguiente animación ilustra esto:
+
+
+
+En Python, el cálculo que se muestra arriba se puede realizar de la siguiente manera:
+
+```
+python
+p = 7
+result = (3 + 5) % p
+print(result) # imprime 1
+```
+
+En este capítulo, siempre que realicemos cálculos, expresaremos nuestro resultado como un número en el rango de $0…(p-1)$, que es el conjunto de elementos en nuestro campo finito `p`. Por ejemplo, 2 * 5 = 10, que “simplificamos” a 3 (módulo 7).
+
+Observe cómo 3 + 5 "desbordó" el límite de 6. **En campos finitos, el desbordamiento no es algo malo, definimos el comportamiento de desbordamiento como parte del cálculo.** En un campo finito módulo 7, 5 + 3 se define como 1.
+
+Los desbordamientos por defecto también se manejan de manera similar. Por ejemplo, $3 - 5 = - 2$, pero en módulo 7 obtenemos $5$ porque $7 - 2 = 5$.
+
+## Cómo funciona la aritmética modular
+
+En un lenguaje de programación típico, escribimos la suma en un cuerpo finito como `(6 + 1) % 7 == 0`, pero en notación matemática, normalmente decimos
+
+$$0 = 6 + 1 \pmod 7$$
+
+O de forma más general,
+
+$$c = a + b \pmod p$$
+
+donde $a$ y $b$ son números en el cuerpo finito, $c$ es el resto que asigna cualquier número $≥ p$ y $< 0 $ al conjunto $\set{0, 1, …, p - 1}$.
+
+La notación $\pmod p$ significa que *toda* la aritmética se realiza módulo $p$. Por ejemplo,
+
+$$a + b = c + d \pmod p$$
+
+Es equivalente (en Python o C) a `a + b % p == c + d % p`.
+
+La multiplicación funciona de manera similar, al multiplicar los números entre sí y luego tomar el módulo:
+
+$$3 = 4 × 6 \pmod 7 = 24 \pmod 7 = 3$$
+
+La operación de multiplicación anterior se puede visualizar de dos maneras:
+
+
+
+O alternativamente:
+
+
+
+Nos referimos a un número en un cuerpo finito como un "elemento".
+
+## $p$ y el orden del cuerpo
+
+El número con el que tomamos el módulo lo llamaremos $p$. En todos nuestros ejemplos es un número primo. En el campo más amplio de las matemáticas, $p$ podría no ser necesariamente primo, pero solo nos ocuparemos de los casos en los que $p$ sea primo.
+
+Debido a esta restricción, el *orden* del cuerpo siempre es igual a $p$. El *orden* es el número de elementos en el cuerpo. El término general para el número con el que tomamos el módulo es la *característica* del cuerpo.
+
+Por ejemplo, si tenemos $p = 5$, los elementos son $\set{0, 1, 2, 3, 4}$. Hay 5 elementos, por lo que el orden de ese campo es 5.
+
+## La identidad de la suma $p$
+
+Cualquier elemento más $p$ es el mismo elemento. Por ejemplo, $(3 + 7) \pmod 7 = 3$. Considere los ejemplos en la siguiente animación:
+
+
+
+## Inverso aditivo
+
+Considere que $5 + (-5) = 0$.
+
+En matemáticas, el inverso aditivo de $a$ es un número $b$ tal que $a + b = 0$. Generalmente, expresamos el inverso aditivo de un número colocando un signo negativo al frente. $-a$ es, por definición, el número que al sumarse con $a$ da como resultado 0.
+
+### Reglas generales de los inversos aditivos
+
+- El cero es su propio inverso aditivo.
+- Cada número tiene exactamente un inverso aditivo
+
+Estas reglas de los inversos aditivos también se aplican a los cuerpos finitos. Aunque no tenemos elementos con signos negativos como $-5$, algunos elementos pueden “comportarse” como números negativos entre sí utilizando el operador módulo.
+
+En aritmética regular, $-5$ es el número que, al sumarse a $5$, da como resultado $0$. Si nuestro cuerpo finito es $p = 7$, entonces $2$ puede considerarse como $-5$ porque $(5 + 2) \pmod 7 = 0$. De manera similar, $5$ puede considerarse como $-2$ porque son el inverso aditivo del otro. Para ser precisos, $-2$ es congruente con $5$ o $-2 \equiv 5 \pmod 7$.
+
+Para calcular el inverso aditivo de un elemento, simplemente calcula $p - a$ donde $a$ es el elemento del que estamos tratando de encontrar el inverso aditivo. Por ejemplo, para encontrar el inverso aditivo de 14 módulo 23, calculamos $23 - 14 = 9$. Podemos ver que $14 + 9 \pmod {23} = 0$. $p$ es congruente con cero, por lo que esto es equivalente a calcular $-5$ como $0 - 5$.
+
+Al igual que con los números reales:
+
+- cada elemento en un campo finito tiene exactamente un inverso aditivo
+- cero es su propio inverso aditivo.
+
+El patrón general para los inversos aditivos en un campo finito es que los elementos en la primera mitad del campo finito son los inversos aditivos de los elementos en la segunda mitad, como se muestra en la figura siguiente. El cero es la excepción ya que es su propio inverso aditivo. Los números conectados por la línea verde son sus inversos aditivos en el campo $p = 7$:
+
+
+
+**Ejercicio:** Supongamos que elegimos un $p \geq 3$. ¿Cuáles valores distintos de cero, si los hay, son sus propios inversos aditivos?
+
+## Inverso multiplicativo
+
+Considere que $5 × (1/5) = 1$.
+
+El inverso multiplicativo de $a$ es un número $b$ tal que $ab = 1$. Cada elemento excepto cero tiene un inverso multiplicativo. Con "números regulares", un inverso multiplicativo es $1 / \text{num}$. Por ejemplo, el inverso multiplicativo de $5$ es $1/5$, y el inverso multiplicativo de $19$ es $1/19$.
+
+Aunque no tenemos números fraccionarios en cuerpos finitos, aún podemos encontrar pares de números que "se comportan como" fracciones cuando se suman o multiplican entre sí.
+
+Por ejemplo, el inverso multiplicativo de $4$ en el cuerpo finito $p = 7$ es $2$, porque $4 * 2 = 8$, y $8 \pmod 7 = 1$. Por lo tanto, $2$ "se comporta" como $1/4$ en el cuerpo finito, o para ser más precisos, $1/4$ es congruente con $2 \pmod 7$.
+
+### Reglas generales de los inversos multiplicativos en la aritmética de cuerpos finitos:
+
+- 0 no tiene un inverso multiplicativo
+- 1 es su propio inverso multiplicativo
+- Cada número (excepto 0) tiene exactamente un inverso multiplicativo (que podría ser él mismo)
+- el elemento de valor $(p - 1)$ es su propio inverso multiplicativo. Por ejemplo, en un cuerpo finito de $p = 103$, $1$ y $102$ son sus propios inversos multiplicativos. En un cuerpo finito de $p = 23$, $1$ y $22$ son sus propios inversos multiplicativos (la razón se explica en la próxima sección). Otro ejemplo: en el cuerpo finito módulo 5, 1 es su propio inverso y 4 es su propio inverso. $4 \times 4 = 16$, y $16 \pmod 5 = 1$.
+
+### Por qué el elemento de valor $p - 1$ es su propio inverso multiplicativo
+
+Cuando multiplicamos $-1$ por sí mismo, obtenemos $1$. Por lo tanto, $-1$ es su propio inverso multiplicativo para números reales. El elemento de valor $(p - 1)$ es congruente con $-1$. Por lo tanto, esperamos que $(p - 1)$ sea su propio inverso multiplicativo, y de hecho ese es el caso.
+
+Otra forma de ver por qué $p - 1$ es su propio inverso multiplicativo es considerar que $(p - 1)(p - 1) = p² - 2p + 1$. Dado que $p$ es congruente con $0$, entonces $p² - 2p + 1$ se simplifica a $0^2 - 2*0 + 1 = 1$.
+
+#### Soluciones para circuitos aritméticos sobre cuerpos finitos
+
+Si consideramos el siguiente circuito aritmético sobre números regulares, esperamos que `x = -1` sea la única asignación satisfactoria.
+
+```python
+x * x === 1
+x + 1 === 0
+```
+
+En un cuerpo finito, la asignación satisfactoria es el elemento congruente con $-1$, o $p - 1$.
+
+### Cálculo del inverso multiplicativo con el pequeño teorema de Fermat
+
+El [pequeño teorema de Fermat](https://en.wikipedia.org/wiki/Fermat%27s_little_theorem) establece que
+
+$$
+a^{p}=a\pmod p, a\neq0
+$$
+
+En otras palabras, si elevas un elemento distinto de cero a $p$, recuperas ese elemento. Algunos ejemplos:
+
+- $3⁵ \pmod 5 = 3$
+- $4⁷ \pmod 7 = 4$
+- $14⁵³ \pmod {53} = 14$
+
+Ahora considere si dividimos ambos lados de $aᵖ = a \pmod p$ por $a$ (recuerde, $a ≠ 0$):
+
+$$a^p=a$$
+$$\frac{a^p}{a}=\frac{a}{a}$$
+$$a^{p-1}=1$$
+
+Podemos escribir el resultado como
+
+$$
+a(a^{p-2}) = 1
+$$
+
+**Esto significa que $aᵖ⁻² \pmod p$ es el inverso multiplicativo de $a$**, ya que $a$ por $aᵖ⁻²$ es 1.
+
+Algunos ejemplos:
+
+- El inverso multiplicativo de $3$ en el cuerpo finito $p = 7$ es $5$. $3⁷⁻² = 5 \pmod 7$
+- El inverso multiplicativo de 8 en el cuerpo finito $p = 11$ es $7$. $8¹¹⁻² = 7 \pmod {11}$
+
+La ventaja de este enfoque es que podemos usar el `expmod` [precompilación en Ethereum](https://www.rareskills.io/post/solidity-precompiles) para calcular el inverso modular en un contrato inteligente.
+
+En la práctica, esta no es una forma ideal de calcular inversos multiplicativos porque elevar un número a una gran potencia es computacionalmente costoso. Las bibliotecas que calculan el inverso multiplicativo usan algoritmos más eficientes en segundo plano. Sin embargo, cuando dicha biblioteca no está disponible y se desea una solución rápida y simple, y calcular un exponente grande no es excesivamente costoso, se puede usar el Pequeño Teorema de Fermat.
+
+## Calcular el inverso multiplicativo con Python
+
+Usando Python 3.8 o posterior, podemos hacer `pow(a, -1, p)` para calcular el inverso multiplicativo de `a` en el cuerpo finito `p`. El primer argumento de `pow` es la base, el segundo es el exponente y el tercero es el módulo.
+
+Ejemplo:
+
+```python
+p = 17
+print(pow(5, -1, p))
+# 7
+assert (5 * 7) % p == 1
+```
+
+**Ejercicio:** Halla el inverso multiplicativo de 3 módulo 5. Solo hay 5 posibilidades, así que pruébalas todas y ve cuáles funcionan.
+
+**Ejercicio:** ¿Cuál es el inverso multiplicativo de 50 en el cuerpo finito $p = 51$? No necesitas Python para calcular esto, consulta los principios descritos en “Reglas generales de los inversos multiplicativos”.
+
+**Ejercicio:** Usa Python para calcular el inverso multiplicativo de 288 en el cuerpo finito de `p = 311`. Puedes comprobar tu trabajo validando que `(288 * respuesta) % 311 == 1`.
+
+## La suma de inversos multiplicativos es consistente con la suma "regular" de fracciones
+
+En un cuerpo finito de `p = 7`, los números 2 y 4 son inversos multiplicativos entre sí porque $(2 \times 4) \pmod 7 = 1$. Esto significa que en el cuerpo finito $p = 7$, $4$ es congruente con $1/2$ y $2$ es congruente con $1/4$.
+
+Decimos que $4$ es congruente con $1/2$ en el cuerpo finito de $p = 7$ porque $2 \times \mathsf{mul\_inv}(2) = 1$. El inverso multiplicativo de $2$ es $4$ en este cuerpo finito, por lo que podemos tratar a $4$ como $1/2$.
+
+Con números reales, si sumamos $1/2 + 1/2$, esperamos obtener $1$. Lo mismo sucede en un cuerpo finito. Como $4$ se "comporta como" $1/2$, esperamos $4 + 4 \pmod 7 = 1$, y de hecho lo hace.
+
+Podemos codificar el número $5/6$ en un cuerpo finito al pensar en él como la operación $5 * (1/6)$, o $5 \times \mathsf{mul\_inv}(6)$.
+
+Considere que $1/2 + 1/3 = 5/6$. Si nuestro campo finito es $p = 7$, entonces $1/2$ es el inverso multiplicativo de $2$, $1/3$ es el inverso multiplicativo de 3, y $5/6$ es $5$ multiplicado por el inverso multiplicativo de 6:
+
+```python
+p = 7
+one_half = pow(2, -1, p)
+one_third = pow(3, -1, p)
+five_over_six = (pow(6, -1, p) * 5) % p
+
+assert (one_half + one_third) % p == five_over_six
+# True
+```
+
+La forma general de calcular una "fracción" en un campo finito es el numerador multiplicado por el inverso multiplicativo del denominador, módulo `p`:
+
+```python
+def calculate_field_element_from_fraction(num, den, p):
+inv_den = pow(den, -1, p)
+return (num * inv_den) % p
+```
+
+No es posible hacer esto cuando el denominador es un múltiplo de `p`. Por ejemplo, $1/7$ no se puede representar en el cuerpo finito $p = 7$ porque `pow(7, -1, 7)` no tiene solución. El módulo toma el resto después de la división, y el resto de $7/7$ es cero, o más generalmente, $7/d$ es cero cuando $d$ es un múltiplo de $7$. El inverso multiplicativo significa que podemos multiplicar un número y su inverso para obtener $1$, pero si uno de los números es cero, no hay nada que podamos multiplicar por cero para obtener 1.
+
+**Ejercicio:** ejecuta `pow(7, -1, 7)` en Python. Deberías ver que se lanza una excepción, `ValueError: la base no es invertible para el módulo dado`. $7$ mod $7$ es igual a cero. No hay nada que podamos multiplicar por cero para obtener $1$.
+
+### La "división" de un cuerpo finito no sufre pérdida de precisión
+
+Si dividimos `1 / 3` en la mayoría de los lenguajes de programación, sufriremos pérdida de precisión porque $0.\overline{3}$ no es representable en binario.
+
+Sin embargo, `1 / 3` en un cuerpo finito es simplemente el inverso multiplicativo de 3.
+
+Esto significa que el circuito aritmético
+
+```rust
+x + y + z === 1;
+x === y;
+y === z;
+```
+
+tiene una solución exacta cuando se realiza en un cuerpo finito. Esto no sería posible de hacer de manera confiable si usáramos números de punto fijo o flotante como tipos de datos para nuestros circuitos aritméticos (considere que sumar 0.33333 + 0.33333 + 0.33333 dará como resultado 0.99999 en lugar de 1).
+
+La siguiente implementación en Python ilustra el circuito:
+
+```python
+p = 11
+
+# x, y, z tienen valor 1/3
+x = pow(3, -1, 11)
+y = pow(3, -1, 11)
+z = pow(3, -1, 11)
+
+assert x == y;
+assert y == z;
+assert (x + y + z) % p == 1
+```
+
+## Los elementos de un campo finito no tienen una noción tradicional de "par" o "impar"
+
+Decimos que un número es "par" si se puede dividir por dos sin residuo.
+
+**En un campo finito, cualquier elemento se puede dividir por 2 sin resto.**
+
+Es decir, "dividir por dos" es en realidad multiplicar por el inverso multiplicativo de 2, y eso siempre dará como resultado otro elemento de campo sin "residuo".
+
+Sin embargo, si tenemos una representación binaria del elemento de campo, entonces podemos verificar si el elemento es par o impar si se convierte a un entero. Si el bit menos significativo es 1, entonces el número es impar (si se interpreta como un entero, no como un elemento de campo finito).
+
+## Biblioteca de campos finitos en Python
+
+Debido a que puede ser un poco tedioso seguir escribiendo `pow` y `% p` en Python, el lector puede desear usar la [biblioteca de Galois](https://pypi.org/project/galois/) en su lugar (los campos finitos a veces se denominan campos de Galois, que se pronuncian "Gal-wah"). Se puede instalar con `python3 -m pip install galois`.
+
+A continuación, traducimos el código de adición de fracciones de la sección anterior $(1/2 + 1/3 = 1/6)$ para usar la biblioteca `galois` en su lugar. La biblioteca sobrescribe los operadores matemáticos para trabajar en un campo finito:
+
+```python
+import galois
+GF7 = galois.GF(7) # GF7 es una clase que encapsula 7
+
+one_half = GF7(1) / GF7(2)
+one_third = GF7(1) / GF7(3)
+five_over_six = GF7(5) / GF7(6)
+
+assert one_half + one_third == five_over_six
+```
+
+La operación `1 / GF(a)` calcula el inverso multiplicativo de `a`.
+
+La biblioteca `galois` puede calcular el inverso de la suma agregando un signo negativo al principio:
+
+```python
+negative_two = -GF(2)
+assert negative_two + GF(2) == 0
+```
+
+## La multiplicación de fracciones también es consistente
+
+Usemos un cuerpo finito `p = 11` para este ejemplo.
+
+Con números regulares sabemos que $1/3 * 1/2 = 1/6$.
+
+Hagamos esta misma operación en un cuerpo finito:
+
+```python
+import galois
+GF = galois.GF(11)
+
+one_third = GF(1) / GF(3)
+one_half = GF(1) / GF(2)
+one_sixth = GF(1) / GF(6)
+
+assert one_third * one_half == one_sixth
+```
+
+**Ejercicio:** use la biblioteca galois para verificar que $3/4 * 1/2 = 3/8$ en el cuerpo finito $p = 17$.
+
+## a × b ≠ 0 para todos los a, b distintos de cero
+
+No es posible multiplicar dos elementos para obtener cero en un cuerpo finito a menos que uno de los elementos sea cero. Esto también es cierto para los números regulares.
+
+Para entender esto, considere el cuerpo finito $p = 7$. Para multiplicar dos números y obtener $0$ como resultado, entonces uno de los términos $a$ debe ser un múltiplo de 7, de modo que $a \pmod 7$ sea cero. Sin embargo, ninguno de $\set{0, 1, 2, 3, 5, 6}$ es un múltiplo de 7, por lo que esto no puede suceder.
+
+Haremos referencia a este hecho con frecuencia cuando diseñemos circuitos aritméticos. Por ejemplo, si sabemos
+
+```python
+x₁ * x₂ * ... * xₙ ≠ 0
+```
+
+Entonces podemos estar seguros de que todas las variables `x₁, x₂, xₙ` son distintas de cero, incluso si no conocemos sus valores.
+
+A continuación, se muestra cómo podemos usar este truco para un circuito aritmético realista. Supongamos que tenemos señales `x₁, x₂, x₃`. Deseamos restringir al menos una de estas señales para que tenga el valor 8 sin especificar cuál lo tiene. Primero calculamos el inverso aditivo de 8 `a_inv(8)` para nuestro campo. Entonces hacemos:
+
+`(x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0`
+
+Esto se podría escribir como
+
+`(x₁ - 8)(x₂ - 8)(x₃ - 8) === 0`
+
+con el entendimiento de que `-8` es el inverso aditivo de 8 para nuestro campo finito.
+
+Siempre que una de las señales tenga el valor 8, entonces ese término será cero y toda la expresión se multiplicará a cero. Este truco se basa en dos hechos:
+
+- Si todos los términos son distintos de cero, no hay forma de que la expresión evalúe a cero
+- El inverso aditivo de 8 es único, y 8 es el inverso aditivo único para el inverso aditivo de 8. En otras palabras, no hay ningún valor excepto 8 que resulte en que 8 + inv(8) sea cero.
+
+Por lo tanto, el circuito aritmético `(x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0` indica que al menos uno de `x₁, x₂, xₙ` tiene el valor 8.
+
+## Las operaciones de cuerpo finito son asociativas, conmutativas y distributivas
+
+Al igual que con las matemáticas regulares, con la aritmética modular, las propiedades asociativa, conmutativa y distributiva se cumplen, es decir,
+
+**asociativa**
+
+$(a + b) + c = a + (b + c) \pmod p$
+
+**suma conmutativa**
+
+$(a + b) = (b + a) \pmod p$
+
+**multiplicación conmutativa**
+
+$ab = ba \pmod p$
+
+**distributiva**
+
+$a(b + c) = ab + ac \pmod p$
+
+## Raíces cuadradas modulares
+
+En "matemáticas regulares", los números cuadrados perfectos tienen raíces cuadradas enteras. Por ejemplo, 25 tiene una raíz cuadrada de 5, 49 tiene una raíz cuadrada de 7, y así sucesivamente.
+
+### Los elementos en un cuerpo finito no necesitan ser cuadrados perfectos para tener una raíz cuadrada
+
+Considere que $5 × 5 \pmod {11} = 3$. Esto significa que la raíz cuadrada de 3 es 5, módulo 11. Debido a la forma en que se envuelven los cuerpos finitos, los elementos de los cuerpos finitos no tienen que ser cuadrados perfectos para tener una raíz cuadrada.
+
+Al igual que las raíces cuadradas regulares, que tienen dos soluciones: una positiva y una negativa, las raíces cuadradas modulares en un cuerpo finito también tienen dos soluciones. La excepción es el elemento 0, que solo tiene 0 como raíz cuadrada.
+
+En el cuerpo finito módulo 11, los siguientes elementos tienen raíces cuadradas:
+
+| Elemento | 1.ª raíz cuadrada | 2.ª raíz cuadrada |
+| -------- | ----------------- | ----------------- |
+| 0 | 0 | n/a |
+| 1 | 1 | 10 |
+| 3 | 5 | 6 |
+| 4 | 2 | 9 |
+| 5 | 4 | 7 |
+| 9 | 3 | 8 |
+
+**Ejercicio**: Verifique que las raíces cuadradas indicadas en la tabla sean correctas en el cuerpo finito módulo 11.
+
+Observe que la segunda raíz cuadrada es siempre la inversa aditiva de la primera raíz cuadrada, al igual que los números reales.
+
+Por ejemplo:
+
+- En matemáticas regulares, las raíces cuadradas de $9$ son $3$ y $-3$, donde ambas son inversas aditivas entre sí.
+- En un cuerpo finito de $p = 11$, las raíces cuadradas de 9 son 3 y 8. 8 es el inverso aditivo de 3 porque $8 + 3 \pmod {11}$ es $0$, así como $3$ es el inverso aditivo de $-3$.
+
+Los elementos 2, 6, 7, 8 y 10 no tienen raíces cuadradas modulares en el cuerpo finito $p = 11$. Esto se puede descubrir elevando al cuadrado cada elemento de 0 a 10 inclusive, y viendo que 2, 6, 7, 8 y 10 nunca se producen.
+
+```python
+numeros_con_raices = set()
+p = 11
+for i in range(0, p):
+numeros_con_raices.add(i * i % p)
+
+print("numeros_con_raices:", numeros_con_raices)
+# numeros_con_raices: {0, 1, 3, 4, 5, 9}
+```
+
+Tenga en cuenta que 3 no es un cuadrado perfecto, pero sí tiene una raíz cuadrada en este cuerpo finito.
+
+### Cálculo de la raíz cuadrada modular
+
+La raíz cuadrada modular se puede calcular en Python con la [biblioteca libnum](https://github.com/hellman/libnum). A continuación, calculamos la raíz cuadrada de 5 módulo 11. El tercer argumento de las funciones `has_sqrtmod_prime_power` y `sqrtmod_prime_power` se puede establecer en 1 para nuestros propósitos.
+
+```python
+# install libnum with `python -m pip install libnum`
+
+from libnum import has_sqrtmod_prime_power, sqrtmod_prime_power
+has_sqrtmod_prime_power(5, 11, 1) # True
+list(sqrtmod_prime_power(5, 11, 1)) # [4, 7]
+# Las raíces cuadradas generalmente tienen dos soluciones. 4 y 7 son las raíces cuadradas de 5 (mod 11)
+```
+
+Cuando `p` se puede escribir como `4k + 3` donde `k` es un entero, entonces la raíz cuadrada modular se puede calcular de la siguiente manera:
+
+```python
+def mod_sqrt(x, p):
+ assert (p - 3) % 4 == 0, "prime not 4k + 3"
+ exponent = (p + 1) // 4
+ return pow(x, exponent, p) # x ^ e % p
+```
+
+La función anterior devuelve una de las raíces cuadradas de x módulo p. La otra raíz cuadrada se puede calcular calculando el inverso aditivo del valor devuelto. Si el número primo no tiene la forma `4k + 3`, entonces se debe utilizar el [algoritmo de Tonelli-Shanks](https://en.wikipedia.org/wiki/Tonelli–Shanks_algorithm) para calcular la raíz cuadrada modular (que implementa la biblioteca libnum anterior).
+
+**La implicación de esto es que el circuito aritmético `x * x === y` puede tener dos soluciones.** Por ejemplo, en un cuerpo finito `p = 11`, podría parecer que el circuito aritmético `x * x === 4` solo admite el valor 2 porque -2 no es un elemento de cuerpo finito. Sin embargo, ¡esa suposición es muy errónea! La asignación `x = 9`, que es congruente con -2, también satisface el circuito.
+
+**Ejercicio:** Utilice el fragmento de código anterior para calcular la raíz cuadrada modular de 5 en el cuerpo finito de `p = 23`. El código solo le dará una de las respuestas. ¿Cómo se puede calcular el otro?
+
+## Sistemas lineales de ecuaciones en cuerpos finitos
+
+Como se señaló en el capítulo anterior, un circuito aritmético es esencialmente un sistema de ecuaciones. Los sistemas lineales de ecuaciones en un cuerpo finito comparten muchas propiedades con un sistema lineal de ecuaciones sobre números regulares. Sin embargo, existen algunas diferencias que inicialmente pueden resultar inesperadas. Dado que los circuitos aritméticos se calculan sobre cuerpos finitos, debemos comprender dónde pueden estar estas desviaciones sorprendentes.
+
+Un [sistema lineal de ecuaciones](https://math.libretexts.org/Bookshelves/Algebra/Algebra_and_Trigonometry_1e_(OpenStax)/11%3A_Systems_of_Equations_and_Inequalities/11.01%3A_Systems_of_Linear_Equations_-_Two_Variables) es una colección de ecuaciones de línea recta con un conjunto de incógnitas (variables) que intentamos resolver juntos. Para encontrar la solución única de un sistema de ecuaciones lineales, debemos hallar un valor numérico para cada variable que satisfaga todas las ecuaciones del sistema simultáneamente.
+
+Los sistemas de ecuaciones lineales con números reales tienen:
+
+1) **Sin solución:** lo que significa que las dos ecuaciones representan líneas que son paralelas en dos dimensiones o que nunca se cruzan en tres dimensiones o más
+
+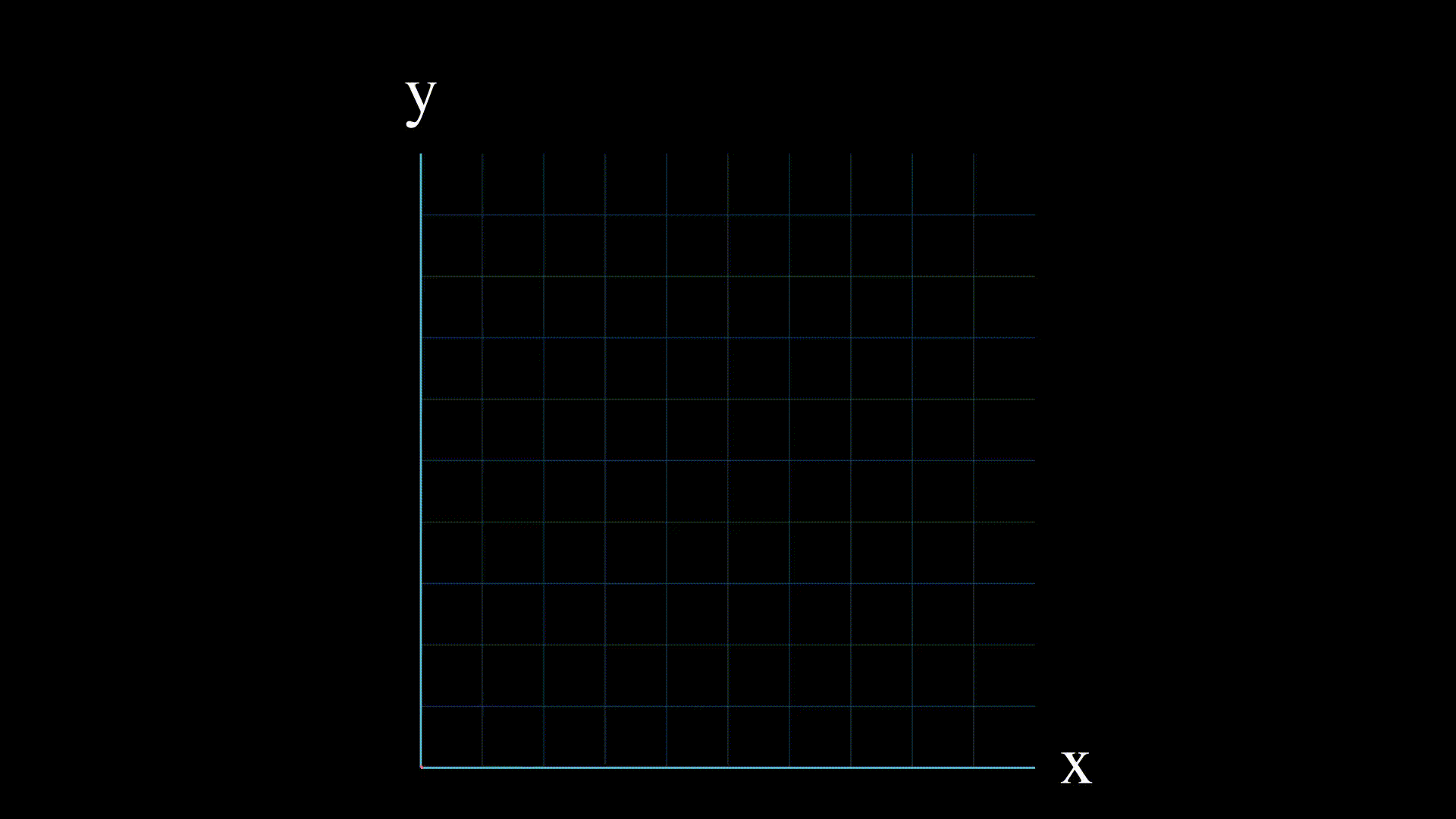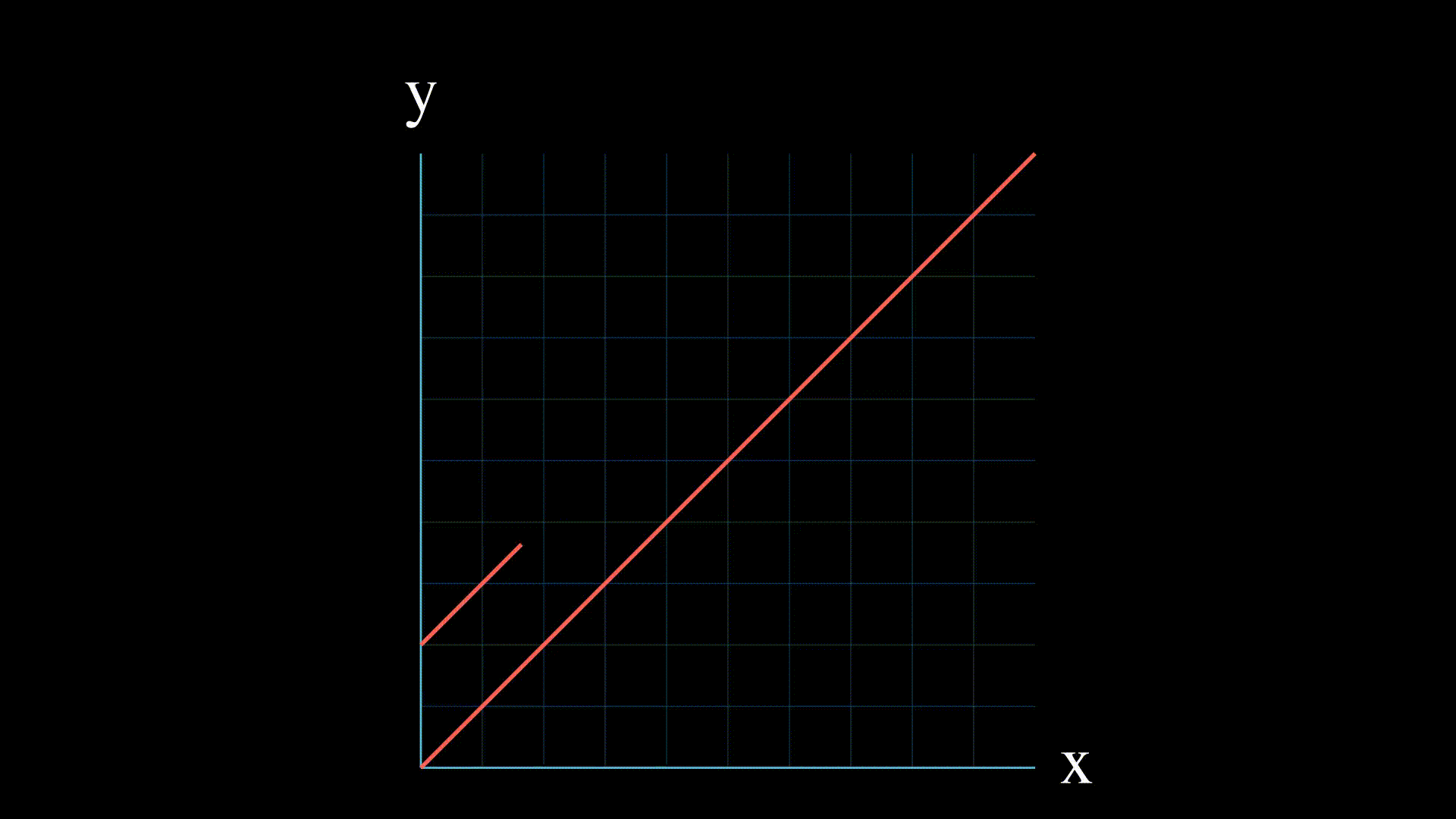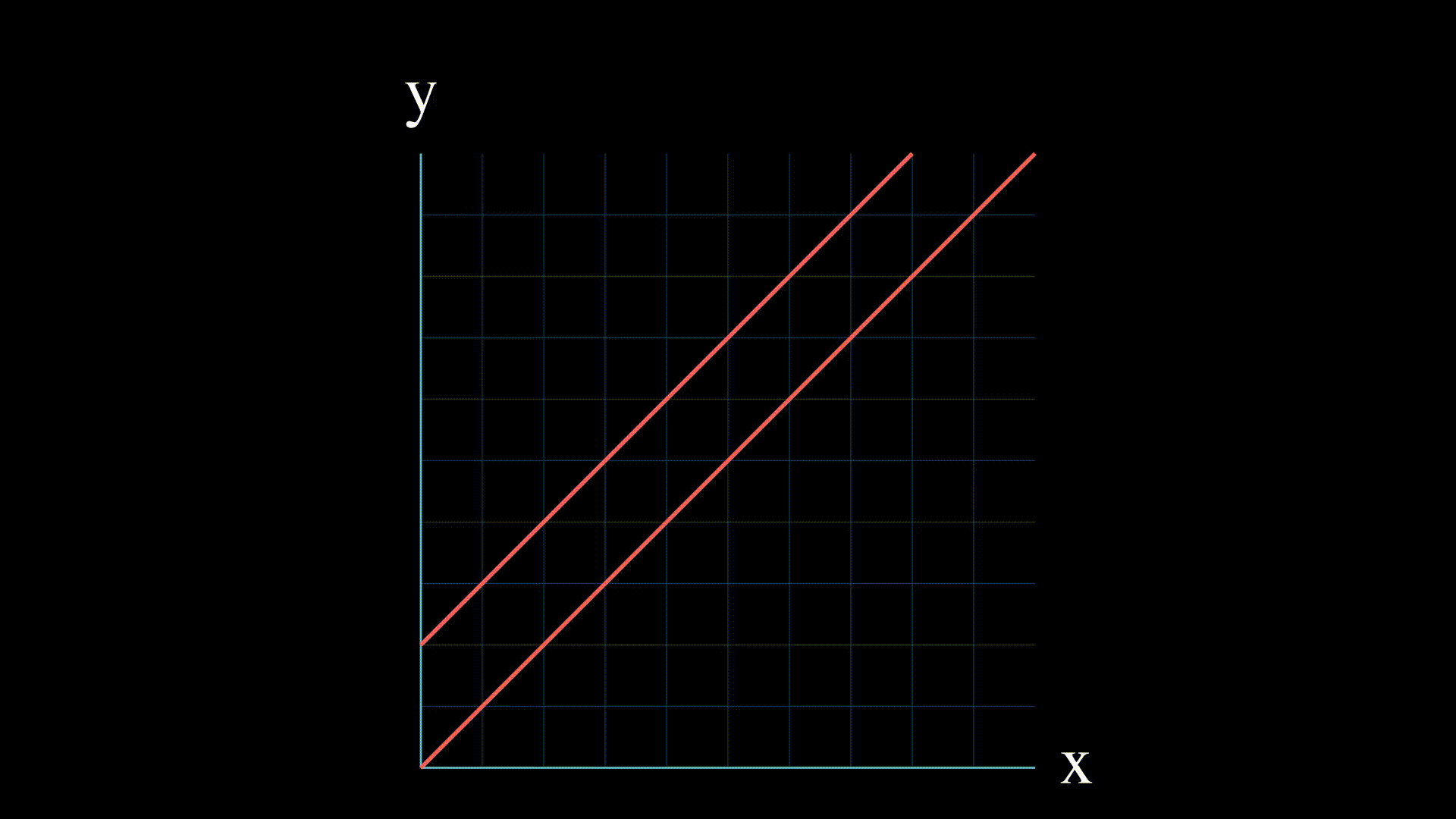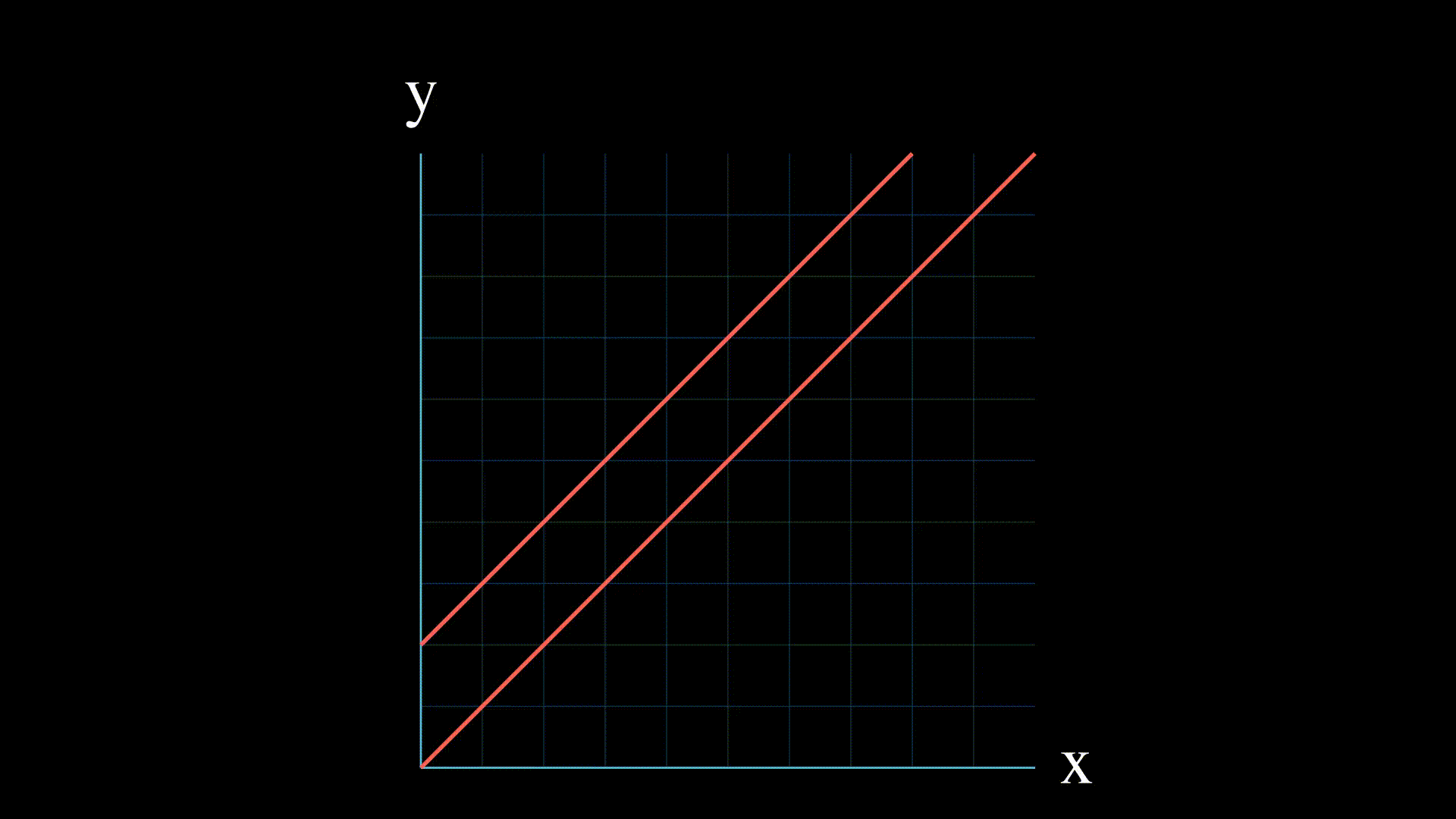
+
+2) **Una solución** lo que significa que las líneas se intersecan en un punto
+
+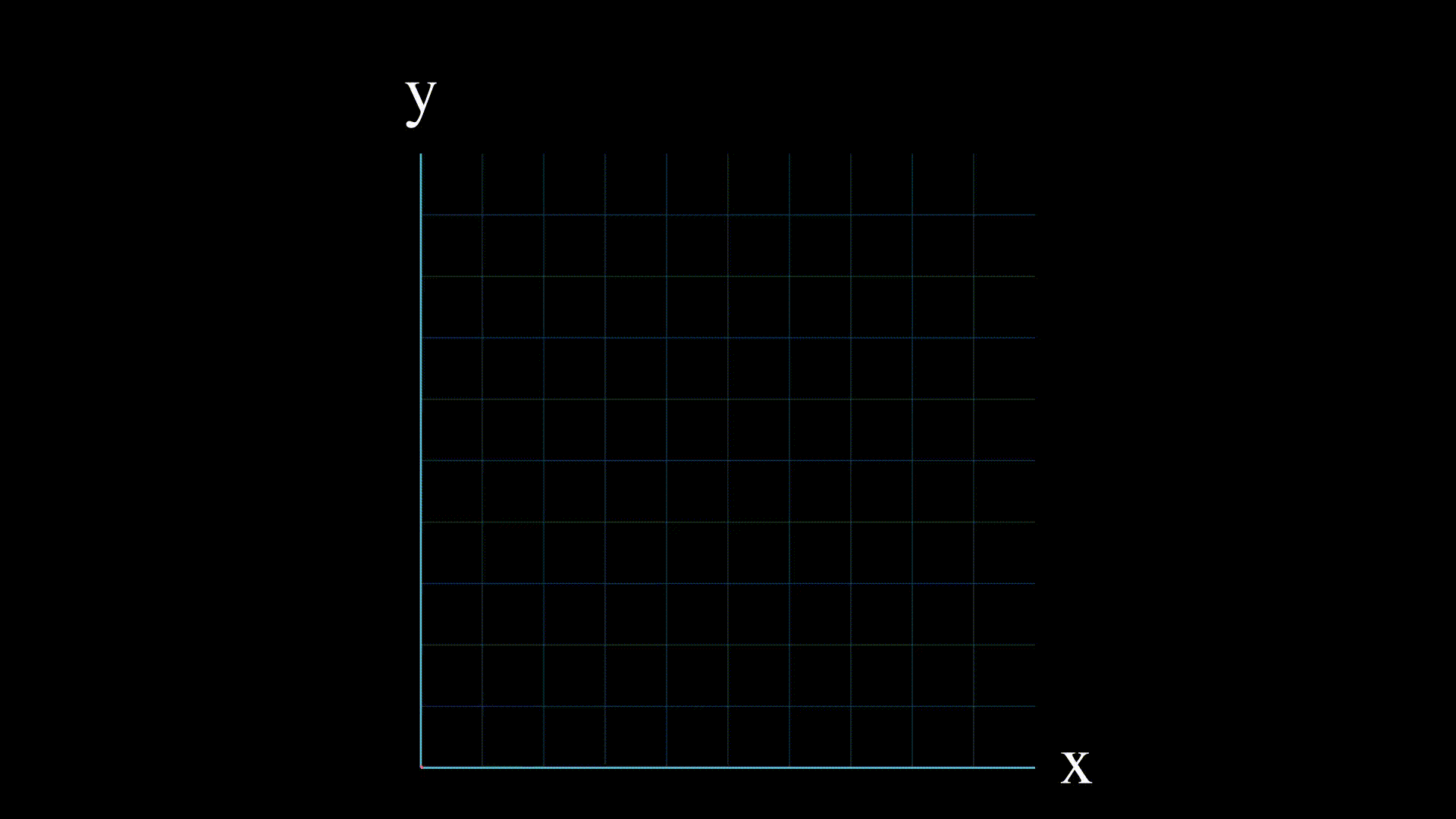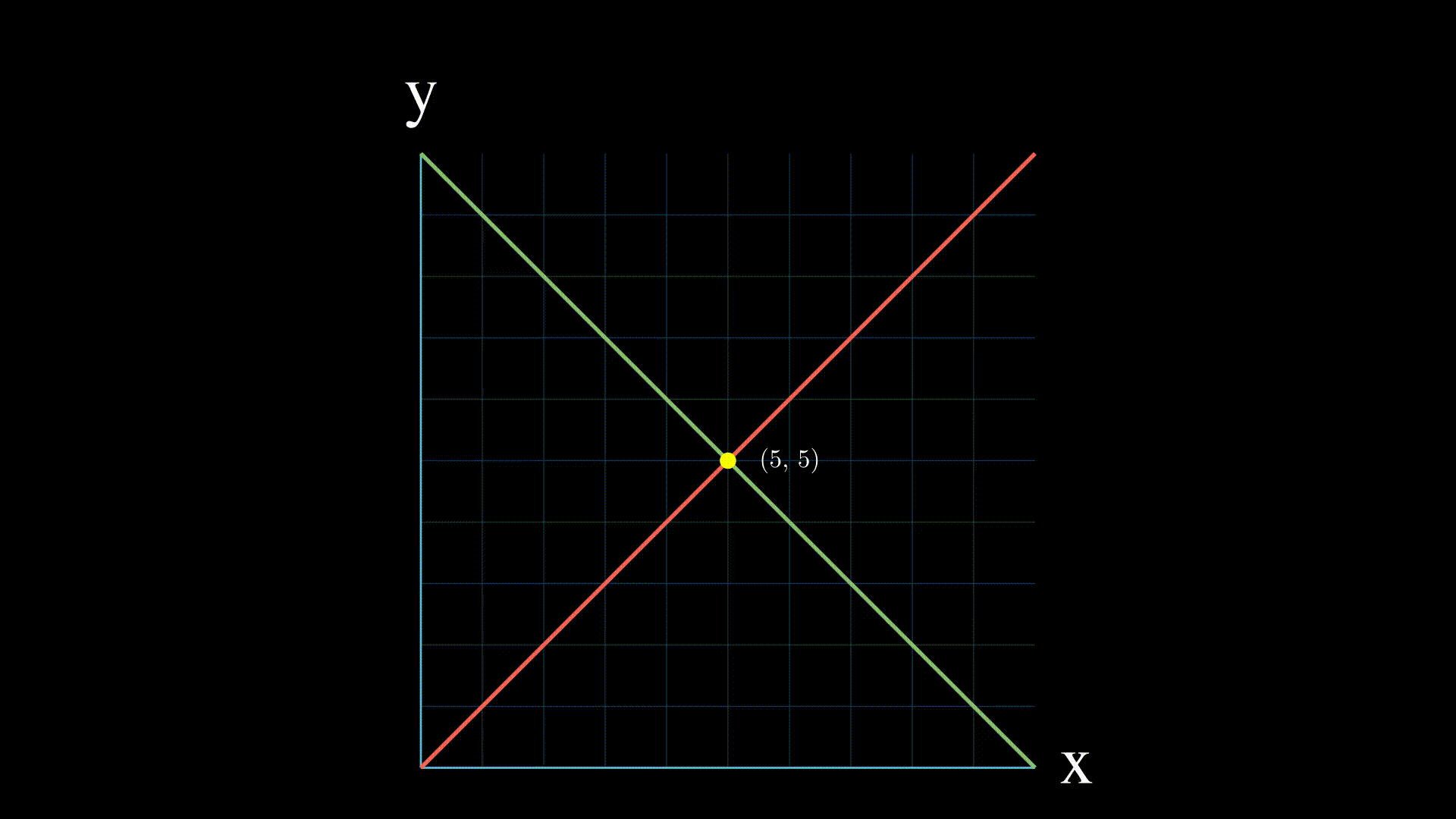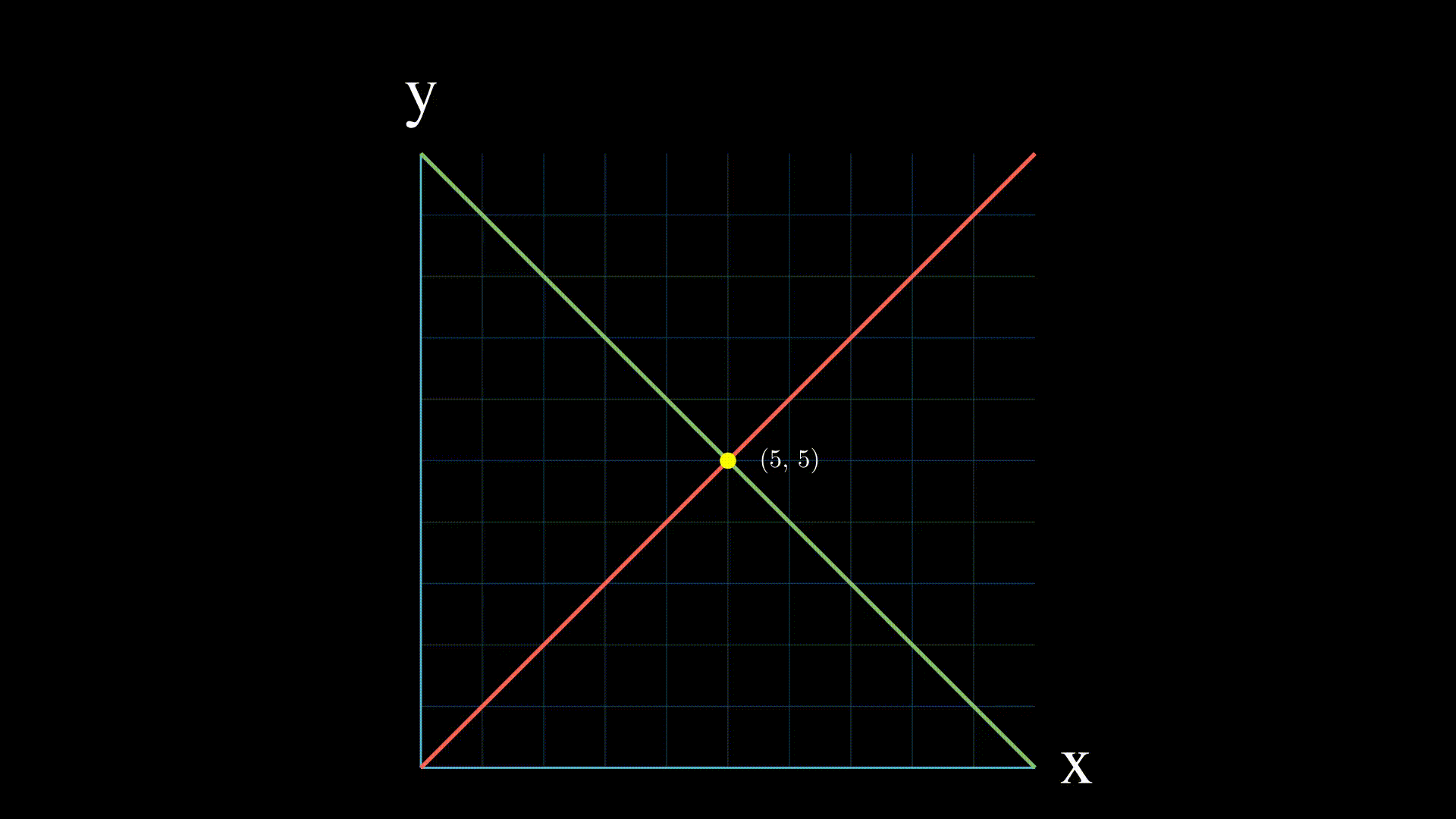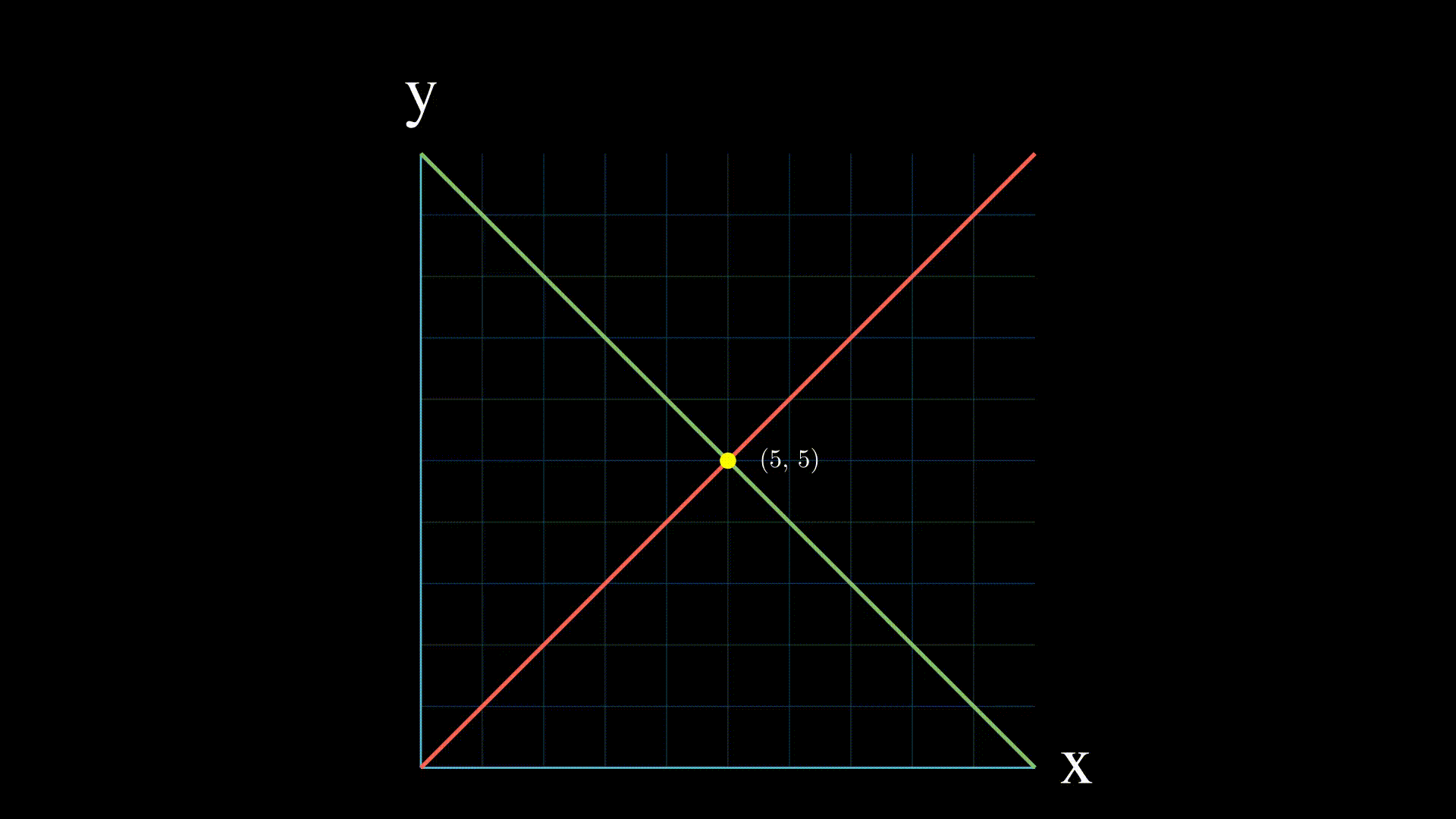
+
+3) **Soluciones infinitas:** si las dos ecuaciones representan la misma línea, entonces hay infinitos puntos de intersección y el sistema de ecuaciones lineal tiene un número infinito de soluciones.
+
+
+
+Los sistemas de ecuaciones de campos finitos también tienen
+
+1. ninguna solución o
+
+2. una solución o
+
+3. $p$ soluciones, es decir, tantas soluciones como el orden del campo
+
+**Sin embargo, el hecho de que un sistema lineal de ecuaciones sobre números reales tenga cero, una o infinitas soluciones *no implica* que el mismo sistema lineal de ecuaciones sobre un campo finito también tendrá cero, una o `p` muchas soluciones.**
+
+La razón por la que enfatizamos esto es porque usamos circuitos aritméticos y una asignación a las señales para codificar nuestra solución a un problema en NP. Sin embargo, debido a que los circuitos aritméticos están codificados con campos finitos, podemos terminar codificando el problema de una manera que no capture el comportamiento de las ecuaciones que estamos tratando de modelar.
+
+Los siguientes tres ejemplos muestran cómo el comportamiento de un sistema de ecuaciones puede cambiar cuando se realiza sobre un campo finito.
+
+### Ejemplo 1: Un sistema de ecuaciones con una solución sobre números regulares puede tener `p` muchas soluciones en un cuerpo finito
+
+Por ejemplo, graficamos:
+
+$$
+x+2y=1\\6x+y=6
+$$
+
+
+
+Tiene una solución: $(1, 0)$ para los números reales números, pero sobre el cuerpo finito $p = 11$, tiene 11 soluciones: $\set{(0, 6), (1, 0), (2, 5), (3, 10), (4, 4), (5, 9), (6, 3), (7, 8), (8, 2), (9, 7), (10, 1)}$.
+
+**¡No suponga que un sistema de ecuaciones (circuito aritmético) que tiene una única solución en números reales tiene una única solución en un cuerpo finito!**
+
+A continuación, graficamos las soluciones de los sistemas de ecuaciones sobre los cuerpos finitos para ilustrar que ambas ecuaciones "se intersecan en todas partes", es decir, tienen el mismo conjunto de puntos que satisfacen ambas ecuaciones:
+
+
+
+Esto puede parecer extremadamente contraintuitivo: veamos cómo sucede. Si resolvemos las ecuaciones originales:
+
+$$
+x+2y=1\\6x+y=6
+$$
+
+para $y$ obtenemos:
+
+$$
+y = 1/2 - 1/2*x\\y=6-6x
+$$
+
+$1/2$ es el inverso multiplicativo de $2$. En un cuerpo finito de $p = 11$, $6$ es el inverso multiplicativo de $2$, es decir, $2 * 6 \pmod {11} = 1$. Por lo tanto, $x + 2y = 1$ y $6x + y = 6$ son en realidad la misma ecuación en el cuerpo finito $p = 11$. Es decir, la ecuación $y = 1/2 - 1/2x$ cuando se codifica en un cuerpo finito es $y = \mathsf{mul\_inv}(2) - \mathsf{mul\_inv}(2)x$ que es $y = 6 - 6x$, que es la misma que la otra ecuación en el sistema.
+
+### Ejemplo 2: Un sistema de ecuaciones con una solución sobre números regulares puede tener cero soluciones en un cuerpo finito
+
+También contraintuitivamente, un sistema de ecuaciones con una única solución sobre números reales puede no tener solución en un cuerpo finito:
+
+$$
+x + 2y=1\\
+7x+3y=2
+$$
+
+
+
+Claramente, este sistema de ecuaciones tiene un punto de intersección, pero sobre un cuerpo finito no tiene solución.
+
+A continuación mostramos el gráfico de las dos ecuaciones en un cuerpo finito:
+
+
+
+**Ejercicio:** Escriba código para aplicar fuerza bruta a cada combinación de `(x, y)` sobre `x = 0..10, y = 0..10` para verificar que el sistema anterior no tiene solución sobre el cuerpo finito campo de `p = 11`.
+
+¿Por qué este sistema de ecuaciones no tiene solución en el campo finito $p = 11$?
+
+Si resolvemos
+
+$$
+x + 2y=1\\7x+3y=2
+$$
+
+para números reales, obtenemos las soluciones
+
+$$
+x = \frac{1}{11},\space y=\frac{5}{11}
+$$
+
+Las fracciones anteriores no tienen un elemento congruente en el campo finito `p = 11`.
+
+Recuerde que dividir por un número es equivalente a multiplicar por su inverso multiplicativo. Además, recuerde que el orden del campo (en este caso 11) no tendrá un inverso multiplicativo, porque el orden del campo es congruente con 0.
+
+El inverso multiplicativo de `a` es el valor `b` tal que `a * b = 1`. Sin embargo, si `a = 0` (o cualquier valor congruente con él) entonces no hay solución para `b`. Por lo tanto, las expresiones que escribimos para las soluciones en los números reales no se pueden traducir a elementos de nuestro cuerpo finito.
+
+Por lo tanto, las soluciones (x, y) anteriores no son parte del cuerpo finito. Por lo tanto, en un cuerpo finito `p = 11`, `x + 2y = 1` y `7x + 3y = 2` son líneas paralelas.
+
+Para ver esto desde otro ángulo, podríamos resolver las ecuaciones para y y obtener:
+
+$$
+y = 1/2 - x/2\\y=2/3-7x/3
+$$
+
+Vimos en la sección anterior que 6 es el inverso multiplicativo de 2, por lo que la primera ecuación tiene una "pendiente" de 6 en el cuerpo finito. En la segunda ecuación, calculamos la pendiente calculando 7 veces el inverso multiplicativo de 3: `(7 * pow(3, -1, 11)) % 11 = 6` . Ahora demostramos que sus pendientes son las mismas en un cuerpo finito.
+
+La pendiente es el coeficiente de `x` en la forma `y = c + bx`. Para las dos ecuaciones anteriores, la primera pendiente es `-1/2` y la segunda pendiente es `-7/3`. Si convertimos ambas fracciones en un elemento del cuerpo finito de `p = 11`, obtenemos el mismo valor de 5:
+
+```python
+import galois
+GF11 = galois.GF(11)
+
+negative_1 = -GF11(1)
+negative_7 = -GF11(7)
+
+slope1 = GF11(negative_1) / GF11(2)
+slope2 = GF11(negative_7) / GF11(3)
+
+assert slope1 == slope2 # 5 == 5
+```
+
+La implicación de este hecho para el circuito aritmético:
+
+```python
+x + 2 * y === 1
+7 * x + 3 * y === 2
+```
+
+es que el circuito aritmético no tiene una asignación satisfactoria en un cuerpo finito `p = 11`.
+
+### Ejemplo 3: Un sistema de ecuaciones con cero soluciones sobre números regulares puede tener `p` soluciones en un cuerpo finito
+
+Las dos fórmulas siguientes trazan líneas que son paralelas y, por lo tanto, no tienen solución sobre números reales:
+
+$$
+x + 2y = 3\\4x + 8y = 1
+$$
+
+
+
+Sin embargo, sobre el cuerpo finito campo `p = 11`, tiene 11 soluciones: $\set{(0, 7), (1, 1), (2, 6), (3, 0), (4, 5), (5, 10), (6, 4), (7, 9), (8, 3), (9, 8), (10, 2)}$. Las soluciones se representan gráficamente a continuación:
+
+
+
+**Ejercicio:** Convierte las dos ecuaciones a su representación en el campo finito y observa que son iguales.
+
+Supongamos que codificamos este sistema de ecuaciones como un circuito aritmético:
+
+$$
+x + 2y = 3\\4x + 8y = 1
+$$
+
+```python
+x + 2 * y === 3
+4 * x + 8 * y === 1
+```
+
+Para el cuerpo finito que estamos usando, nuestras restricciones son redundantes aunque "se vean diferentes". Es decir, dos restricciones que se ven diferentes en realidad restringen a $x$ e $y$ a tener los mismos valores.
+
+## Polinomios en cuerpos finitos
+
+En el capítulo sobre circuitos aritméticos, usamos el polinomio `x(x - 1) === 0` para hacer cumplir que `x` solo puede ser 0 o 1. Esto podría escribirse como una ecuación polinómica. Para hacerlo, expandimos completamente nuestra expresión hasta que se exprese como potencias separadas de x, cada una multiplicada por un coeficiente. En este caso: `x² - x === 0`.
+
+La suposición de que el polinomio `x² - x === 0` solo tiene soluciones 0 o 1 en un cuerpo finito (así como con números reales) es válida en este caso. Sin embargo, en general, no se debe suponer que las raíces de un polinomio sobre números reales tengan las mismas raíces en un cuerpo finito. Mostraremos algunos contraejemplos más adelante.
+
+Sin embargo, los polinomios en cuerpos finitos comparten muchas propiedades con los polinomios sobre números reales:
+
+- Un polinomio de grado $d$ tiene como máximo $d$ raíces. Las raíces de un polinomio $p(x)$ son los valores $r$ tales que $p(r) = 0$.
+- Si sumamos dos polinomios $p_1$ y $p_2$, el grado de $p_1 + p_2$ será como máximo $\max(\deg(p_1), \deg(p_2))$. Es posible que el grado de $p_1 + p_2$ sea menor que $\max(\deg(p_1), \deg(p_2))$. Por ejemplo, $p_1=x³ + 5x + 7$, y $p_2 = -x³$,
+- La suma de polinomios en un cuerpo finito sigue las leyes asociativas, conmutativas y distributivas.
+- Si multiplicamos dos polinomios $p_1$ y $p_2$, las raíces del producto serán la unión de las raíces de $p_1$ y $p_2$.
+
+Dibujemos como ejemplo $y = x² \pmod {17}$.
+
+
+
+El dominio de $x$ son los elementos del campo finito, y la salida (rango) también debe ser un miembro del campo finito. Es decir, observe cómo todos los valores de $x$ e $y$ se encuentran en el intervalo de $[0,16]$. Un polinomio sobre un cuerpo finito solo puede tener valores $x$ e $y$ menores que $p$.
+
+El equivalente de $y = -x²$ en el cuerpo finito $p = 17$ es $y = 16x² \pmod 17$ ya que 16 es el inverso aditivo de 1 en ese cuerpo finito. El polinomio $y = 16x² \pmod {17}$ se representa gráficamente a continuación:
+
+
+
+### Los polinomios que no tienen raíces en números reales pueden tener raíces en un cuerpo finito
+
+Al igual que nuestros ejemplos anteriores con sistemas de ecuaciones lineales, no se debe asumir que un polinomio con ciertas raíces en números reales tiene las mismas raíces en un cuerpo finito.
+
+A continuación, graficamos $y = x² + 1$ en el cuerpo finito $p = 17$. En números reales, $y = x² + 1$ no tiene raíces reales. Pero en un cuerpo finito, tiene dos raíces en $4$ y $13$, marcadas con puntos rojos a continuación:
+
+
+
+Expliquemos ahora por qué $y = x² + 1$ no tiene raíces en números reales, pero sí en el cuerpo finito $p = 17$. En el cuerpo finito $p = 17$, 17 es congruente con cero. Por lo tanto, si introducimos un valor en $x$ de modo que $x² + 1$ se convierta en $17$, el polinomio dará como resultado cero, no $17$. Podemos resolver $x² + 1 = 17$ para $x² = 17 - 1 = 16$. En un cuerpo finito de $p = 17$, $x² = 16$ tiene soluciones $4$ y $13$. Por lo tanto, $y = x² + 1$ tiene raíces $4$ y $13$ en el cuerpo finito $p = 17$.
+
+### Los polinomios con raíces reales pueden no tener raíces en un cuerpo finito
+
+Consideremos el polinomio $y = x² − 5$. Podemos ver que tiene raíces en $\sqrt{5}$ y $-\sqrt{5}$. Sin embargo, si lo graficamos sobre un cuerpo finito módulo 17, podemos ver que nunca cruza el eje x:
+
+
+
+No hay raíces porque $\sqrt{5}$ no se puede representar en un cuerpo finito módulo 17. Sin embargo, en el cuerpo finito $p = 11$, entonces habría dos raíces porque 5 tiene raíces cuadradas modulares en el cuerpo finito de $p = 11$.
+
+### Limitaciones en circuitos aritméticos para demostraciones ZK
+
+Si deseamos escribir un circuito aritmético para mostrar "Sé la raíz del polinomio $y = x² − 5$" usando un circuito aritmético sobre un cuerpo finito, entonces podemos encontrarnos con el problema de no poder codificar $\sqrt{5}$. Es decir, sobre números reales, $y = x² − 5$ tiene una raíz de $\sqrt{5}$, pero esto no se puede expresar en algunos cuerpos finitos. Dependiendo de $p$, el circuito aritmético `x² === 5` puede no tener ningún testigo satisfactorio.
+
+### Polinomios en cuerpos finitos con Python
+
+Al experimentar con circuitos aritméticos, a veces es útil escribir código Python para simularlos. Cuando nuestro circuito aritmético tiene una forma polinómica, podemos usar la biblioteca `galois` de antes para probar su comportamiento. Los siguientes ejemplos de código ilustran cómo usar esta biblioteca para trabajar con polinomios.
+
+### Sumar polinomios en un cuerpo finito
+
+En el código a continuación, definimos dos polinomios: `p1 = x² + 2x + 102` y `p2 = x² + x + 1` y luego los sumamos simbólicamente para producir `2x² + 3x`. Tenga en cuenta que los términos de coeficiente constante suman cero en el cuerpo finito `p = 103`.
+
+```python
+import galois
+GF103 = [galois.GF](http://galois.gf/)(103) # p = 103
+
+# definimos un polinomio x^2 + 2x + 102 mod 103
+p1 = galois.Poly([1,2,102], GF103)
+
+print(p1)
+# x^2 + 2x + 102
+
+# definimos un polinomio x^2 + x + 1 mod 103
+p2 = galois.Poly([1,1,1], GF103)
+
+print(p1 + p2)
+# 2x^2 + 3x
+```
+
+La biblioteca `galois` es lo suficientemente inteligente como para interpretar números enteros negativos como inversos aditivos, como lo demuestra el código a continuación:
+
+```python
+import galois
+GF103 = galois.GF(103) # p = 13
+
+# Podemos ingresar "-1" como coeficiente, y esto se calculará
+# automáticamente como `p - 1`
+# -1 se convierte en 102 en un campo p = 103
+p3 = galois.Poly([-1, 1], GF103)
+p4 = galois.Poly([-1, 2], GF103)
+
+print(p3)
+# 102x + 1
+print(p4)
+# 102x + 2
+```
+
+### Multiplicación de polinomios en un campo finito
+
+Podemos multiplicar polinomios entre sí:
+
+```python
+print(p3 * p4)
+# x^2 + 100x + 2
+```
+
+Tenga en cuenta que `p3` y `p4` son polinomios de grado 1 y su producto es de grado 2 polinomio.
+
+### Encontrar las raíces de un polinomio en un cuerpo finito
+
+Encontrar las raíces de polinomios en cuerpos finitos es un tema aparte (consulte la página de Wikipedia para conocer los algoritmos sobre [factorización de polinomios en cuerpos finitos](https://en.wikipedia.org/wiki/Factorization_of_polynomials_over_finite_fields)). La biblioteca `galois` puede calcular las raíces con la función `roots`. Esto puede ser útil para verificar que las restricciones aritméticas en forma polinómica realmente creen las restricciones deseadas.
+
+```python
+print((p3 * p4).roots())
+# [1, 2]
+```
+
+### Problemas con la biblioteca `galois`
+
+La biblioteca toma silenciosamente el valor mínimo de los números de punto flotante que se pasan como coeficientes:
+
+```python
+# La biblioteca galois convertirá silenciosamente
+# los números de punto flotante en un entero
+galois.Poly([2.5], GF103)
+# Poly(2, GF(103))
+```
+
+La biblioteca revertirá si se pasa un número mayor o igual a `p`:
+
+```python
+# El siguiente código falla porque no podemos
+# tener coeficientes del orden del campo o mayor
+galois.Poly([103], GF103)
+# ValueError: las matrices GF(103) deben tener elementos en `0 <= x < 103`, no [103].
+```
+
+## Obtenga más información con RareSkills
+
+Consulte nuestro [Libro ZK](https://www.rareskills.io/zk-book) para obtener más información sobre las pruebas de conocimiento cero
+
+## Problemas de práctica
+
+En los problemas a continuación, use un campo finito `p` de `21888242871839275222246405745257275088548364400416034343698204186575808495617`. Tenga en cuenta que la biblioteca `galois` tarda un tiempo en inicializar un objeto `GF`, `galois.GF(p)`, de este tamaño.
+
+1. Un desarrollador crea un circuito aritmético `x * y * z === 0` y `x + y + z === 0` con la intención de restringir todas las señales a cero. Encuentra un contraejemplo de esto donde se satisfacen las restricciones, pero no todos los valores de `x`, `y` y `z` son 0.
+2. Un desarrollador crea un circuito con el polinomio `x² + 2x + 3 === 11` y demuestra que 2 es una solución. ¿Cuál es la otra solución? Pista: escribe el circuito como `x² + 2x - 8 === 0` y luego factoriza el polinomio a mano para encontrar las raíces. Finalmente, calcula el elemento congruente de las raíces en el cuerpo finito para encontrar la otra solución.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
\ No newline at end of file
diff --git a/spanish-es/groth16_es.md b/spanish-es/groth16_es.md
new file mode 100644
index 0000000..8da2b14
--- /dev/null
+++ b/spanish-es/groth16_es.md
@@ -0,0 +1,526 @@
+# Groth16 explicado
+
+El algoritmo Groth16 permite que un probador calcule un programa aritmético cuadrático sobre puntos de curva elíptica derivados en una configuración confiable y que un verificador lo verifique rápidamente. Utiliza puntos de curva elíptica auxiliares de la configuración confiable para evitar pruebas falsificadas.
+
+## Requisitos previos
+
+Este artículo es un capítulo del [Libro ZK Proofs de RareSkills](https://www.rareskills.io/zk-book). Se supone que está familiarizado con los capítulos anteriores.
+
+## Notación
+
+Nos referimos a un [punto de curva elíptica](https://www.rareskills.io/post/elliptic-curves-finite-fields) que pertenece al grupo de curvas elípticas $\mathbb{G}_1$ como $[x]_1$ y a un punto de curva elíptica que pertenece al grupo de curvas elípticas $\mathbb{G}_2$ como $[x]_2$. Un [emparejamiento](https://www.rareskills.io/post/bilinear-pairing) entre $[x]_1$ y $[x]_2$ se denota como $[x]_1\bullet[x]_2$ y produce un elemento en $\mathbb{G}_{12}$. Las variables en negrita como $\mathbf{a}$ son vectores, las letras mayúsculas en negrita como $\mathbf{L}$ son matrices y los elementos de campo (a veces denominados informalmente "escalares") son letras minúsculas como $d$. Todas las operaciones aritméticas ocurren en un [campo finito](https://www.rareskills.io/post/finite-fields) con una característica que es igual al orden del grupo de curvas elípticas.
+
+Dado un [Circuito Aritmético (Circuito ZK)](https://www.rareskills.io/post/arithmetic-circuit), lo convertimos en un [Sistema de Restricciones de Rango 1 (R1CS)](https://www.rareskills.io/post/rank-1-constraint-system) $\mathbf{L}\mathbf{a}\circ \mathbf{R}\mathbf{a} = \mathbf{O}\mathbf{a}$ con matrices de dimensión $n$ filas y $m$ columnas con un vector testigo $\mathbf{a}$. Luego, podemos convertir el R1CS en [Programa Aritmético Cuadrático (QAP)](https://www.rareskills.io/post/quadratic-arithmetic-program) interpolando las columnas de las matrices como valores $y$ sobre los valores $x$ $[1,2,...,n]$. Como $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$ tienen $m$ columnas, terminaremos con tres conjuntos de $m$ polinomios:
+
+$$
+\begin{array}{}
+u_1(x),...,u_m(x) & m \text{ polinomios interpolados en las }m \text{ columnas de } \mathbf{L}\\
+v_1(x),...,v_m(x)& m \text{ polinomios interpolados en las }m \text{ columnas de } \mathbf{R}\\
+w_1(x),...,w_m(x)& m \text{ polinomios interpolados en las }m \text{ columnas de } \mathbf{O}\\
+\end{array}
+$$
+
+A partir de esto, podemos construir un programa aritmético cuadrático (QAP):
+
+$$
+\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) = \sum_{i=1}^m a_iw_i(x) + h(x)t(x)
+$$
+
+donde
+
+$$
+t(x) = (x - 1)(x - 2)\dots(x - n)
+$$
+
+y
+
+$$
+h(x) = \frac{\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) - \sum_{i=1}^m a_iw_i(x)}{t(x)}
+$$
+
+Si un tercero crea una cadena de referencia estructurada (srs) a través de una ceremonia de potencias de tau, entonces el probador puede evaluar los términos de suma (los términos $\sum a_if_i(x)$) en el QAP en un punto oculto $\tau$. Calculemos las cadenas de referencia estructuradas de la siguiente manera:
+
+$$
+\begin{align*}
+[\Omega_{n-1}, \Omega_{n-2},\dots,\Omega_2,\Omega_1,G_1] &= [\tau^nG_1,\tau^{n-1}G_1,\dots,\tau G_1,G_1] && \text{srs para } G_1 \\
+[\Theta_{n-1}, \Theta_{n-2},\dots,\Theta_2,\Theta_2,G_2] &= [\tau^nG_2,\tau^{n-1}G_2,\dots,\tau G_2,G_2] && \text{srs para } G_2\\
+[\Upsilon_{n-2},\Upsilon_{n-3},\dots,\Upsilon_1,\Upsilon_0]&=[\tau^{n-2}t(\tau)G_1,\tau^{n-3}t(\tau)G_1,\dots,\tau t(\tau)G_1,t(\tau)G_1] && \text{srs para }h(\tau)t(\tau)\\
+\end{align*}
+$$
+
+Nos referimos a $f(\tau)$ como un polinomio evaluado en una cadena de referencia estructurada $[\tau^dG_1,...,\tau^2G_1,\tau G_1,G_1]$ a través del producto interno:
+
+$$
+f(\tau) = \sum_{i=1}^d f_i\Omega_i=\langle[f_d, f_{d-1},...,f_1,f_0],[\Omega_d,\Omega_{d-1},...,G_1]\rangle
+$$
+
+o para $\mathbb{G}_2$ srs:
+
+$$
+f(\tau) = \sum_{i=1}^d f_i\Theta_i=\langle[f_d, f_{d-1},...,f_1,f_0],[\Theta_d,\Theta_{d-1},...,G_1]\rangle
+$$
+
+$f(\tau)$ es una abreviatura de la expresión anterior y produce un punto de curva elíptica. No significa que el demostrador conozca $\tau$.
+
+El probador puede evaluar su QAP en la configuración confiable calculando:
+
+$$
+\begin{align*}
+[A]_1 &= \sum_{i=1}^m a_iu_i(\tau)\\
+[B]_2 &= \sum_{i=1}^m a_iv_i(\tau)\\
+[C]_1 &= \sum_{i=1}^m a_iw_i(\tau) + h(\tau)t(\tau)
+\end{align*}
+$$
+
+Los detalles de este cálculo se analizan en nuestro tutorial [Programas aritméticos cuadráticos sobre curvas elípticas](https://www.rareskills.io/post/elliptic-curve-qap).
+
+Si el QAP está equilibrado, entonces se cumple la siguiente ecuación:
+
+$$
+[A]_1\bullet[B]_2 \stackrel{?}= [C]_1\bullet G_2
+$$
+
+## Motivación
+
+La simple presentación de $([A]_1, [B]_2, [C]_1)$ no es un argumento convincente de que el probador conoce $\mathbf{a}$ de modo que el QAP está balanceado.
+
+El probador puede simplemente inventar valores $a$, $b$, $c$ donde $ab = c$, calcular
+
+$$
+\begin{align*}
+[A]_1 &= aG_1\\
+[B]_2 &= bG_2\\
+[C]_1 &= cG_1
+\end{align*}
+$$
+
+y presentarlos como puntos de curva elíptica $[A]_1$, $[B]_2$, $[C]_1$ al verificador.
+
+Por lo tanto, el verificador no tiene idea de si $([A]_1, [B]_2, [C]_1)$ fueron el resultado de un QAP satisfecho o no.
+
+Necesitamos obligar al probador a ser honesto sin introducir demasiada carga computacional. El primer algoritmo que logró esto fue "[Pinocchio: Nearly Practical Verifiable Computation](https://eprint.iacr.org/2013/279.pdf)." Esto fue lo suficientemente útil para que ZCash basara la primera versión de su cadena de bloques en él.
+
+Sin embargo, Groth16 pudo lograr lo mismo en muchos menos pasos, y el algoritmo todavía se usa ampliamente en la actualidad, ya que ningún algoritmo desde entonces ha producido un algoritmo tan eficiente para el paso de verificación (aunque otros algoritmos han eliminado la configuración confiable o han reducido significativamente la cantidad de trabajo para el probador).
+
+**Actualización para 2024:** Un artículo titulado de manera bastante triunfal "[Polymath: Groth16 is not the limit](https://eprint.iacr.org/2024/916)" publicado en Cryptology demuestra un algoritmo que requiere menos pasos de verificación que Groth16. Sin embargo, no se conocen implementaciones del algoritmo en este momento.
+
+## Prevención de falsificaciones Parte 1: Introducción a $\alpha$ y $\beta$
+
+### Una fórmula de verificación "irresoluble"
+
+Supongamos que actualizamos nuestra fórmula de verificación a la siguiente:
+
+$$[A]_1 \bullet [B]_2 \stackrel{?}= [D]_{12} + [C]_1\bullet G_2$$
+
+*Tenga en cuenta que estamos usando notación aditiva para el grupo $G_{12}$ por conveniencia.*
+
+Aquí, $[D]_{12}$ es un elemento de $G_{12}$ y tiene un logaritmo discreto desconocido.
+
+Ahora demostramos que es imposible para un verificador proporcionar una solución $([A]_1, [B]_2, [C]_1)$ a esta ecuación, sin conocer el logaritmo discreto de $[D]_{12}$.
+
+#### Ataque 1: falsificar A y B y derivar C
+
+Supongamos que el verificador selecciona aleatoriamente $a’$ y $b’$ para producir $[A]₁$ y $[B]₂$ e intenta derivar un valor $[C’]$ que sea compatible con la fórmula del verificador.
+
+$$[A]_1 \bullet [B]_2 \stackrel{?}= [D]_{12} + [C]_1\bullet G_2$$
+
+Conociendo los logaritmos discretos de $[A]₁$ y $[B]₂$, el probador malicioso intenta resolver $[C’]$ haciendo
+
+$$\begin{align*}\underbrace{[A]_1\bullet [B]_2 - [D]_{12}}_{\chi_{12}}=[C']_1\bullet G_2\\
+[\chi]_{12}=[C']_1\bullet G_2
+\end{align*}$$
+
+La línea final requiere que el probador resuelva el logaritmo discreto de $\chi_{12}$, por lo que no puede calcular un logaritmo discreto válido para $[C']_1$.
+
+#### Ataque 2: falsificar C y derivar A y B
+
+Aquí el demostrador elige un punto aleatorio $c'$ y calcula $[C']_1$. Como conocen $c'$, pueden intentar descubrir una combinación compatible de $a'$ y $b'$ tal que
+
+$$\begin{align*}[A]_1 \bullet [B]_2 &\stackrel{?}= \underbrace{[D]_{12} + [C]_1\bullet G_2}_{[\zeta]_{12}}\\
+[A]_1 \bullet [B]_2 &\stackrel{?}=[\zeta]_{12}
+\end{align*}$$
+
+Esto requiere que el demostrador, dado $[\zeta]_{12}$, encuentre un $[A]₁$ y un $[B]₂$ que se emparejen para producir $[\zeta]_{12}$.
+
+De manera similar al problema del logaritmo discreto, nos basamos en suposiciones criptográficas no demostradas de que este cálculo (descomponer un elemento en $\mathbb{G}_{12}$ en un elemento $\mathbb{G}_1$ y $\mathbb{G}_2$) es inviable. En este caso, la suposición de que no podemos descomponer $[\zeta]_{12}$ en $[A]₁$ y $[B]₂$ se denomina *Suposición Diffie-Hellman Bilineal*. El lector interesado puede ver una discusión relacionada sobre la [Suposición Diffie-Hellman Decisional](https://en.wikipedia.org/wiki/Decisional_Diffie–Hellman_assumption).
+
+(No probado no significa poco confiable. Si puede encontrar una manera de probar o refutar esta suposición, ¡lo esperan la fama y la fortuna! En la práctica, no se conoce ninguna manera de descomponer $[\zeta]_{12}$ en $[A]₁$ y $[B]₂$ y se cree que es computacionalmente inviable).
+
+### Cómo se usan $\alpha$ y $\beta$
+
+En la práctica, Groth16 no usa un término $[D]_{12}$. En cambio, la configuración confiable genera dos escalares aleatorios $\alpha$ y $\beta$ y publica los puntos de la curva elíptica $([\alpha]_1,[\beta]_2)$ calculados como:
+
+$$
+\begin{align*}
+[α]_1 &= α G_1 \\
+[β]_2 &= β G_2
+\end{align*}
+$$
+
+Lo que llamamos $[D]_{12}$ es simplemente $[\alpha]_1 \bullet [\beta]_2$.
+
+### Nueva derivación de las fórmulas de demostración y verificación
+
+Para que la fórmula de verificación $[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1\bullet[\beta]_2 + [C]_1\bullet G_2$ sea "soluble", debemos modificar nuestra fórmula QAP para incorporar $\alpha$ y $\beta$.
+
+$$\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) = \sum_{i=1}^m a_iw_i(x) + h(x)t(x)$$
+
+Ahora consideremos qué sucede si introducimos los términos $\theta$ y $\eta$ en el lado izquierdo de la ecuación:
+
+$$(\boxed{\theta}+\sum_{i=1}^m a_iu_i(x))(\boxed{\eta} +\sum_{i=1}^m a_iv_i(x)) =$$
+$$=\boxed{\theta\eta} + \boxed{\theta}\sum_{i=1}^m a_iv_i(x) + \boxed{\eta}\sum_{i=1}^m a_iu_i(x) + \sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x)$$
+
+Podemos sustituir los términos más a la derecha utilizando la definición original de QAP:
+$$=\theta\eta + \theta\sum_{i=1}^m a_iv_i(x) + \eta\sum_{i=1}^m a_iu_i(x) + \boxed{\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x)}$$
+
+$$=\theta\eta + \theta\sum_{i=1}^m a_iv_i(x) + \eta\sum_{i=1}^m a_iu_i(x) + \boxed{\sum_{i=1}^m a_iw_i(x) + h(x)t(x)}$$
+
+Ahora podemos introducir un QAP "expandido" con lo siguiente definición:
+
+$$(\theta+\sum_{i=1}^m u_i(x))(\eta +\sum_{i=1}^m v_i(x)) =\theta\eta + \theta\sum_{i=1}^m a_iv_i(x) + \eta\sum_{i=1}^m a_iu_i(x) + \sum_{i=1}^m a_iw_i(x) + h(x)t(x)$$
+
+Como adelanto de hacia dónde nos dirigimos, si reemplazamos $\theta$ con $[\alpha]_1$ y $\eta$ con $[\beta]_2$, obtenemos la fórmula de verificación actualizada de antes:
+
+$$[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [C]_1\bullet G_2$$
+
+donde
+
+$$\underbrace{([\alpha]_1+\sum_{i=1}^m a_iu_i(\tau))}_{[A]_1}\underbrace{([\beta]_2 +\sum_{i=1}^m a_iv_i(\tau))}_{[B]_2} =[\alpha]_1\bullet[\beta]_2 + (\underbrace{\alpha\sum_{i=1}^m a_iv_i(\tau) + \beta\sum_{i=1}^m a_iu_i(\tau) + \sum_{i=1}^m a_iw_i(\tau) + h(\tau)t(\tau)}_{[C]_1}) \bullet G_2$$
+
+El demostrador puede calcular $[A]_1$ y $[B]_2$ sin saber $\tau$, $\alpha$ o $\beta$. Dada la cadena de referencia estructurada (potencias de $\tau$) y los puntos de la curva elíptica $([α]_1,[β]_2)$, el probador calcula $[A]_1$ y $[B]_2$ como
+
+$$
+\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau)\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau)\\
+\end{align*}
+$$
+
+Aquí, $a_iu_i(\tau)$ no significa que el probador conozca $\tau$. El probador está usando la cadena de referencia de estructura $[\tau^{n-1}G_1,\tau^{n-2}G_1,\dots,\tau G_1,G_1]$ para calcular $u_i(\tau)$ para $i=1,2,\dots,m$ y las srs $G_2$ para $[B]_2$.
+
+Sin embargo, actualmente no es posible calcular $[C]_1$ sin conocer $\alpha$ y $\beta$. El probador no puede emparejar $[\alpha]_1$ con $\sum a_iu_i(\tau)$ y $[\beta]_2$ con $\sum a_iv_i(\tau)$ porque eso crearía un punto $\mathbb{G}_{12}$, mientras que el probador necesita un punto $\mathbb{G}_1$ para $[C]_1$.
+
+En cambio, la configuración confiable necesita calcular previamente $m$ polinomios para el término $C$ problemático del QAP expandido.
+
+$$\alpha\sum_{i=1}^m a_iv_i(\tau) + \beta\sum_{i=1}^m a_iu_i(\tau) + \sum_{i=1}^m a_iw_i(\tau)$$
+
+Con alguna manipulación algebraica, combinamos los términos de suma en una única suma:
+
+$$=\sum_{i=1}^m (\alpha a_iv_i(\tau)+\beta a_iu_i(\tau) + a_iw_i(\tau))$$
+
+y factorizamos $a_i$:
+
+$$=\sum_{i=1}^m a_i\boxed{(\alpha v_i(\tau)+\beta u_i(\tau) + w_i(\tau))}$$
+
+La configuración confiable puede crear $m$ polinomios evaluados en $\tau$ a partir de la término enmarcado arriba, y el probador puede usarlo para calcular la suma. Los detalles exactos se muestran en la siguiente sección.
+
+### Resumen del algoritmo hasta ahora
+
+#### Pasos de configuración confiable
+
+Concretamente, la configuración confiable calcula lo siguiente:
+$$\begin{align*}
+\alpha,\beta,\tau &\leftarrow \text{escalares aleatorios}\\
+[\tau^{n-1}G_1,\tau^{n-2}G_1,\dots,\tau G_1,G_1] &\leftarrow \text{srs para } \mathbb{G}_1\\
+[\tau^{n-1}G_2,\tau^{n-2}G_2,\dots,\tau G_2,G_2] &\leftarrow \text{srs para } \mathbb{G}_2\\
+[\tau^{n-2}t(\tau),\tau^{n-3}t(\tau),\dots,\tau t(\tau),t(\tau)] &\leftarrow \text{srs para }h(\tau)t(\tau)\\
+[\Psi_1]_1 &= (\alpha v_1(\tau) + \beta u_1(\tau) + w_1(\tau))G_1\\
+[\Psi_2]_1 &= (\alpha v_2(\tau) + \beta u_2(\tau) + w_2(\tau))G_1\\
+&\vdots\\
+[\Psi_m]_1 &= (\alpha v_m(\tau) + \beta u_m(\tau) + w_m(\tau))G_1\\
+\end{align*}$$
+
+La configuración confiable publica
+
+$$([\alpha]_1,[\beta]_2,\text{srs}_{G_1},\text{srs}_{G_2}[\Psi_1]_1,[\Psi_2]_1,\dots,[\Psi_m]_1)$$
+
+#### Pasos del probador
+
+El probador calcula
+
+$$\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau)\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau)\\
+[C]_1 &= \sum_{i=1}^m a_i[\Psi_i]_1 + h(\tau)t(\tau)\\
+\end{align*}$$
+
+Tenga en cuenta que reemplazamos el Polinomio "problemático"
+
+$$=\sum_{i=1}^m a_i\boxed{(\alpha v_i(\tau)+\beta u_i(\tau) + w_i(\tau))}$$
+
+(el que contenía $\alpha$ y $\beta$) con
+
+$$\sum_{i=1}^m a_i[\Psi_i]_1$$
+
+#### Pasos del verificador
+
+El verificador calcula:
+
+$$[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [C]_1\bullet G_2$$
+
+## Compatibilidad con entradas públicas
+
+Hasta ahora, la fórmula del verificador no admite entradas públicas, es decir, hacer pública una parte del testigo.
+
+Por convención, las partes públicas del testigo son los primeros $\ell$ elementos del vector $\mathbf{a}$. Para hacer públicos esos elementos, el verificador simplemente los revela:
+
+$$[a_1, a_2, \dots, a_\ell]$$
+
+Para que el verificador pruebe que esos valores se utilizaron de hecho, debe realizar algunos de los cálculos que el verificador estaba haciendo originalmente.
+
+En concreto, el probador calcula:
+
+$$\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau)\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau)\\
+[C]_1 &= \sum_{i=\ell+1}^m a_i[\Psi_i]_1 + h(\tau)t(\tau)\\
+\end{align*}$$
+
+Obsérvese que solo cambió el cálculo de $[C]_1$: el probador solo utiliza los términos $a_i$ y $\Psi_i$ $\ell + 1$ a $m$.
+
+El verificador calcula los primeros términos $\ell$ de la suma:
+$$[X]_1=\sum_{i=1}^\ell a_i\Psi_i$$
+
+Y la ecuación de verificación es:
+
+$$[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [X]_1\bullet G_2 + [C]_1\bullet G_2$$
+
+## Parte 2: Separación de las entradas públicas de las entradas privadas con $\gamma$ y $\delta$
+
+La suposición en la ecuación anterior es que el probador solo está usando $\Psi_{\ell+1}$ a $\Psi_m$ para calcular $[C]_1$, pero nada impide que un probador deshonesto use $\Psi_1$ a $\Psi_{\ell}$ para calcular $[C]_1$, lo que posiblemente lleve a una prueba falsificada.
+
+Para evitar esto, la configuración confiable introduce nuevos escalares $\gamma$ y $\delta$ para forzar que $\Psi_{\ell+1}$ a $\Psi_m$ estén separados de $\Psi_1$ a $\Psi_{\ell}$. Para hacer esto, la configuración confiable divide (multiplica por el inverso modular) los términos privados (que constituyen $[C]_1$) por $\delta$ y los términos públicos (que constituyen $[X]_1$, la suma que calcula el verificador) por $\gamma$.
+
+Dado que el término $h(\tau)t(\tau)$ está incrustado en $[C]_1$, esos términos también deben dividirse por $\delta$.
+
+$$\begin{align*}
+\alpha,\beta,\tau,\gamma,\delta &\leftarrow \text{escalares aleatorios}\\
+[\tau^{n-1}G_1,\tau^{n-2}G_1,\dots,\tau G_1,G_1] &\leftarrow \text{serie para } \mathbb{G}_1\\
+[\tau^{n-1}G_2,\tau^{n-2}G_2,\dots,\tau G_2,G_2] &\leftarrow \text{serie para } \mathbb{G}_2\\
+[\frac{\tau^{n-2}t(\tau)}{\delta},\frac{\tau^{n-3}t(\tau)}{\delta},\dots,\frac{\tau t(\tau)}{\delta},
+\frac{t(\tau)}{\delta}] &\leftarrow \text{srs para }h(\tau)t(\tau)\\
+\\
+&\text{parte pública del testigo}\\
+[\Psi_1]_1 &= \frac{\alpha v_1(\tau) + \beta u_1(\tau) + w_1(\tau)}{\gamma}G_1\\
+[\Psi_2]_1 &= \frac{\alpha v_2(\tau) + \beta u_2(\tau) + w_2(\tau)}{\gamma}G_1\\
+&\vdots\\
+[\Psi_\ell]_1 &= \frac{\alpha v_m(\tau) + \beta u_m(\tau) + w_m(\tau)}{\gamma}G_1\\
+\\
+&\text{parte privada del testigo}\\
+[\Psi_{\ell+1}]_1 &= \frac{\alpha v_{\ell+1}(\tau) + \beta u_{\ell+1}(\tau) + w_{\ell+1}(\tau)}{\delta}G_1\\
+[\Psi_{\ell+2}]_1 &= \frac{\alpha v_{\ell+2}(\tau) + \beta u_{\ell+2}(\tau) + w_{\ell+2}(\tau)}{\delta}G_1\\
+&\vdots\\
+[\Psi_{m}]_1 &= \frac{\alpha v_{m}(\tau) + \beta u_{m}(\tau) + w_{m}(\tau)}{\delta}G_1\\
+\end{align*}$$
+
+La configuración confiable publica
+$$([\alpha]_1,[\beta]_2,[\gamma]_2,[\delta]_2,\text{srs}_{G_1},\text{srs}_{G_2},[\Psi_1]_1,[\Psi_2]_1,\dots,[\Psi_m]_1)$$
+
+Los pasos del probador son los mismos que antes:
+
+$$\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau)\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau)\\
+[C]_1 &= \sum_{i=\ell+1}^m a_i[\Psi_i]_1 + h(\tau)t(\tau)\\
+\end{align*}$$
+
+Y los pasos del verificador ahora incluyen el emparejamiento por $[\gamma]_2$ y $[\delta]_2$ para cancelar los denominadores:
+
+$$[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [X]_1\bullet [\gamma]_2 + [C]_1\bullet [\delta]_2$$
+
+## Parte 3: Imposición de un verdadero conocimiento cero: r y s
+
+Nuestro esquema aún no es verdaderamente de conocimiento cero. Si un atacante puede adivinar nuestro vector de testigos (lo cual es posible si solo hay un pequeño rango de entradas válidas, por ejemplo, votación secreta de direcciones privilegiadas), entonces puede verificar que su suposición es correcta comparando su prueba construida con la prueba original.
+
+Como ejemplo trivial, supongamos que nuestra afirmación es $x_1$ y $x_2$ son ambos $0$ o $1$. El circuito aritmético correspondiente sería
+
+$$
+\begin{align*}
+x_1 (x_1 - 1) = 0\\
+x_2 (x_2 - 1) = 0
+\end{align*}
+$$
+
+Un atacante solo necesita adivinar cuatro combinaciones para averiguar cuál es el testigo. Es decir, adivina un testigo, genera una prueba y ve si su respuesta coincide con la prueba original.
+
+Para evitar adivinar, el probador necesita "salar" su prueba, y la ecuación de verificación debe modificarse para acomodar la sal.
+
+El probador toma muestras de dos elementos de campo aleatorios $r$ y $s$ y los agrega a $A$ y $B$ para hacer que el testigo sea imposible de adivinar: un atacante tendría que adivinar tanto el testigo como las sales $r$ y $s$:
+
+$$
+\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau) + r[\delta]_1\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau) + s[\delta]_2\\
+[B]_1 &= [\beta]_1 + \sum_{i=1}^m a_iv_i(\tau) + s[\delta]_1\\
+[C]_1 &= \sum_{i=\ell+1}^m a_i[\Psi_i]_1 + h(\tau)t(\tau) + As+Br-rs[\delta]_1\\
+\end{align*}
+$$
+
+Para derivar la fórmula de verificación final, ignoremos temporalmente que no sabemos los logaritmos discretos de los términos de las letras griegas y calculamos el lado izquierdo de la ecuación de verificación $AB$:
+
+$$\underbrace{(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)}_A \underbrace{(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)}_B$$
+
+Desarrollando los términos obtenemos:
+
+$$
+\alpha\beta+\alpha\sum_{i=1}^m a_iv_i(x)+\alpha s\delta + \beta\sum_{i=1}^m a_iu_i(x) + \sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x)+\sum_{i=1}^m a_iu_i(x) s\delta + r\delta\beta + r\delta\sum_{i=1}^m a_iv_i(x) + r\delta s\delta
+$$
+
+Podemos seleccionar los términos originales para $C$
+
+$$
+\alpha\beta+\boxed{\alpha\sum_{i=1}^m a_iv_i(x)}+\alpha s\delta + \boxed{\beta\sum_{i=1}^m a_iu_i(x)} + \boxed{\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x)}+\sum_{i=1}^m a_iu_i(x) s\delta + r\delta\beta + r\delta\sum_{i=1}^m a_iv_i(x) + r\delta s\delta
+$$
+
+Y combinar a la izquierda, dejando los nuevos términos a la derecha:
+
+$$
+\alpha\beta + \boxed{\alpha\sum_{i=1}^m a_iv_i(x) + \beta\sum_{i=1}^m a_iu_i(x) + \sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x)}+ \underline{\alpha s\delta + \sum_{i=1}^m a_iu_i(x) s\delta + r\delta\beta + r\delta\sum_{i=1}^m a_iv_i(x) + r\delta s\delta}
+$$
+
+Reordenamos aún más los términos subrayados para escribirlos en términos de $As\delta$ y $Br\delta$ de la siguiente manera. También dividimos $r\delta s\delta$ en $rs\delta^2 + rs\delta^2 - rs\delta^2$:
+
+$$
+=\alpha s\delta + \sum_{i=1}^m a_iu_i(x) s\delta + rs\delta^2 + r\delta\beta + r\delta\sum_{i=1}^m a_iv_i(x) + rs\delta^2 - rs\delta^2
+$$
+
+Agrupamos los términos $s$ y $r$:
+$$
+=(\alpha s\delta + \sum_{i=1}^m a_iu_i(x) s\delta + rs\delta^2) + (r\delta\beta + r\delta\sum_{i=1}^m a_iv_i(x) + rs\delta^2) - rs\delta^2
+$$
+
+Factoriza $s\delta$ y $r\delta$:
+$$
+=\underbrace{(\alpha+ \sum_{i=1}^m a_iu_i(x) + r\delta)s\delta}_{As\delta} + \underbrace{(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)r\delta}_{Br\delta} - rs\delta^2
+$$
+
+Sustituye $A$ y $B$:
+$$
+=As\delta + Bs\delta - rs\delta
+$$
+
+Entonces nuestra ecuación final es
+
+$$(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)=\alpha\beta+\sum_{i=1}^m a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x)) + h(x)t(x) + As\delta + Bs\delta - rs\delta$$
+
+Ahora lo dividimos en las partes pública y privada:
+
+$$(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)=\alpha\beta+\underbrace{\sum_{i=1}^\ell a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x))}_\text{public} + \underbrace{\sum_{i=\ell+1}^m a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x)) + h(x)t(x) + As\delta + Bs\delta - rs\delta}_\text{private}$$
+
+Queremos que la parte pública y la parte privada estén separadas por $\gamma$ y $\delta$ respectivamente:
+
+$$(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)=\alpha\beta+\gamma\frac{\sum_{i=1}^\ell a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x))}{\gamma} + \delta\frac{\sum_{i=\ell+1}^m a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x)) + h(x)t(x) + As\delta + Bs\delta - rs\delta}{\delta}$$
+
+$\delta$ se cancela para algunos de los términos:
+
+$$(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)=\alpha\beta+\gamma\frac{\sum_{i=1}^\ell a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x))}{\gamma} + \delta\frac{\sum_{i=\ell+1}^m a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x)) + h(x)t(x)}{\delta} + As + Bs - rs\delta$$
+
+Ahora separamos esta ecuación en las partes del verificador y del probador. Los términos enmarcados son la parte del verificador, los términos entre llaves son los términos que proporciona el demostrador:
+
+$$\underbrace{(\alpha + \sum_{i=1}^m a_iu_i(x) + r\delta)}_{[A]_1}\underbrace{(\beta + \sum_{i=1}^m a_iv_i(x) + s\delta)}_{[B]_2}=\boxed{\alpha\beta}+\boxed{\gamma}\boxed{\frac{\sum_{i=1}^\ell a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x))}{\gamma}} + \boxed{\delta}\underbrace{\frac{\sum_{i=\ell+1}^m a_i(\alpha v_i(x) + \beta u_i(x)+w_i(x)) + h(x)t(x)}{\delta} + As + Bs - rs\delta}_{[C]_1}$$
+
+## Algoritmo de prueba Groth16
+
+Ahora estamos listos para mostrar el algoritmo Groth16 de principio a fin.
+
+### Configuración confiable
+
+$$\begin{align*}
+\alpha,\beta,\tau,\gamma,\delta &\leftarrow \text{escalares aleatorios}\\
+[\tau^{n-1}G_1,\tau^{n-2}G_1,\dots,\tau G_1,G_1] &\leftarrow \text{srs for } \mathbb{G}_1\\
+[\tau^{n-1}G_2,\tau^{n-2}G_2,\dots,\tau G_2,G_2] &\leftarrow \text{srs for } \mathbb{G}_2\\
+[\frac{\tau^{n-2}t(\tau)}{\delta},\frac{\tau^{n-3}t(\tau)}{\delta},\dots,\frac{\tau t(\tau)}{\delta},
+\frac{t(\tau)}{\delta}] &\leftarrow \text{srs para }h(\tau)t(\tau)\\
+\\
+&\text{parte pública del testigo}\\
+[\Psi_1]_1 &= \frac{\alpha v_1(\tau) + \beta u_1(\tau) + w_1(\tau)}{\gamma}G_1\\
+[\Psi_2]_1 &= \frac{\alpha v_2(\tau) + \beta u_2(\tau) + w_2(\tau)}{\gamma}G_1\\
+&\vdots\\
+[\Psi_\ell]_1 &= \frac{\alpha v_m(\tau) + \beta u_m(\tau) + w_m(\tau)}{\gamma}G_1\\
+\\
+&\text{parte privada del testigo}\\
+[\Psi_{\ell+1}]_1 &= \frac{\alpha v_{\ell+1}(\tau) + \beta u_{\ell+1}(\tau) + w_{\ell+1}(\tau)}{\delta}G_1\\
+[\Psi_{\ell+2}]_1 &= \frac{\alpha v_{\ell+2}(\tau) + \beta u_{\ell+2}(\tau) + w_{\ell+2}(\tau)}{\delta}G_1\\
+&\vdots\\
+[\Psi_{m}]_1 &= \frac{\alpha v_{m}(\tau) + \beta u_{m}(\tau) + w_{m}(\tau)}{\delta}G_1\\
+\end{align*}$$
+
+La configuración confiable publica
+$$([\alpha]_1,[\beta]_1[\beta]_2,[\gamma]_2,[\delta]_1[\delta]_2,\text{srs}_{G_1},\text{srs}_{G_2},[\Psi_1]_1,[\Psi_2]_1,\dots,[\Psi_m]_1)$$
+
+### Pasos del probador
+
+El probador tiene un testigo $\mathbf{a}$ y genera números aleatorios escalares $r$ y $s$.
+$$\begin{align*}
+[A]_1 &= [\alpha]_1 + \sum_{i=1}^m a_iu_i(\tau)+r[\delta]_1\\
+[B]_1 &= [\beta]_1 + \sum_{i=1}^m a_iv_i(\tau)+s[\delta]_1\\
+[B]_2 &= [\beta]_2 + \sum_{i=1}^m a_iv_i(\tau)+s[\delta]_2\\
+[C]_1 &= \sum_{i=\ell+1}^m a_i[\Psi_i]_1 + h(\tau)t(\tau)+[A]_1s+[B]_2r-rs[\delta]_1\\
+\end{align*}$$
+
+El demostrador publica $([A]_1, [B]_2, [C]_1, [a_1,...,a_\ell])$.
+
+### Pasos del verificador
+
+El verificador verifica
+
+$$
+\begin{align*}
+[X]_1&=\sum_{i=1}^\ell a_i\Psi_i\\
+[A]_1\bullet[B]_2 &\stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [X]_1\bullet [\gamma]_2 + [C]_1\bullet [\delta]_2
+\end{align*}
+$$
+
+## Verificación de Groth16 en Solidity
+
+En este punto, tienes el conocimiento suficiente para comprender el código de verificación de pruebas en Solidity. Aquí se encuentra el código de verificación de prueba de Tornado Cash (https://github.com/tornadocash/tornado-core/blob/master/contracts/Verifier.sol#L192). Se recomienda al lector que lea atentamente el código fuente. Si el lector se siente cómodo con la programación en ensamblador de Solidity, comprender este código fuente no será difícil, ya que los nombres de las variables son consistentes con los de este artículo.
+
+También hay soporte de biblioteca para [Groth16 en Solana] (https://lib.rs/crates/groth16-solana).
+
+## Problemas de seguridad que se deben tener en cuenta
+
+### Groth16 es maleable
+
+Las pruebas de Groth16 son maleables. Dada una prueba válida
+
+$([A]_1, [B]_2, [C]_1)$, un atacante puede calcular la negación puntual de $[A]_1$ y $[B]_2$ y presentar una nueva prueba como $([A']_1, [B']_2, [C]_1)$ donde $[A']_1 = \mathsf{neg}([A]_1)$ y $[B']_2 = \mathsf{neg}([B]_2)$.
+
+Para ver que $[A]_1\bullet[B]_2 = [A']_1\bullet[B']_2$, considere el siguiente código:
+
+```python
+from py_ecc.bn128 import G1, G2, multiplicar, neg, eq, pairing
+
+# elegido arbitrariamente
+x = 10
+y = 100
+A = multiplicar(G1, x)
+B = multiplicar(G2, y)
+
+A_p = neg(A)
+B_p = neg(B)
+
+assert eq(pairing(B, A), pairing(B_p, A_p))
+```
+
+Intuitivamente, el atacante está multiplicando $A$ y $B$ por $-1$, y $(-1)\times(-1)$ se cancela a sí mismo en el emparejamiento.
+
+Por lo tanto, si la fórmula de verificación acepta
+$$[A]_1\bullet[B]_2 \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [X]_1\bullet [\gamma]_2 + [C]_1\bullet [\delta]_2$$
+
+entonces también aceptará
+
+$$\mathsf{neg}([A]_1)\bullet\mathsf{neg}([B]_2) \stackrel{?}= [\alpha]_1 \bullet [\beta]_2 + [X]_1\bullet [\gamma]_2 + [C]_1\bullet [\delta]_2$$
+
+La defensa contra este ataque se describe en la siguiente sección.
+
+Puede ver una prueba de concepto de este ataque en este [artículo](https://medium.com/@cryptofairy/exploring-vulnerabilities-the-zksnark-malleability-attack-on-the-groth16-protocol-8c80d13751c5).
+
+### El probador puede crear una cantidad ilimitada de pruebas para el mismo testigo
+
+Esto no es un "problema de seguridad" en sí mismo: es necesario para lograr el Conocimiento Cero. Sin embargo, la aplicación necesita un mecanismo para rastrear qué hechos ya se han probado y no puede depender de la singularidad de la prueba para lograrlo.
+
+## Obtenga más información con RareSkills
+
+Nuestra capacidad para publicar material como este de forma gratuita depende del apoyo continuo de nuestros estudiantes. Considere inscribirse en nuestro [Zero Knowledge Bootcamp](https://www.rareskills.io/zk-bootcamp), [Web3 Bootcamps](https://www.rareskills.io/web3-blockchain-bootcamps) o conseguir un trabajo en [RareTalent](https://www.raretalent.xyz).
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/group-theory_es.md b/spanish-es/group-theory_es.md
new file mode 100644
index 0000000..77330f1
--- /dev/null
+++ b/spanish-es/group-theory_es.md
@@ -0,0 +1,271 @@
+# Teoría elemental de grupos para programadores
+
+
+
+Este artículo proporciona varios ejemplos de grupos algebraicos para que puedas hacerte una idea de ellos.
+
+Un grupo es un conjunto con:
+
+- un operador binario cerrado
+- el operador binario también es asociativo
+- un elemento identidad
+- cada elemento tiene una inversa
+
+También analizamos los grupos abelianos. Un grupo abeliano tiene el requisito adicional de que el operador binario sea conmutativo
+
+Ahora es momento de analizar los grupos como una estructura matemática.
+
+Un aspecto confuso sobre el uso de números enteros bajo la adición como ejemplo de un grupo es que los estudiantes suelen responder con "pero ¿no puedes multiplicar también números enteros?"
+
+Es cierto que esto es confuso. Hay otras estructuras algebraicas que esperan dos operadores binarios (anillos y cuerpos), pero por ahora piense en un grupo bajo un operador binario fijo e inmutable y, desde la perspectiva del grupo, cualquier otro operador binario posible no existe o no es una preocupación.
+
+Aquí es donde se vuelve aún más confuso. A veces, los operadores binarios son otros operadores binarios disfrazados.
+
+Por ejemplo, cuando se trata de grupos que solo tienen adición, a veces los escritores se refieren casualmente a la multiplicación aunque el grupo no tenga ese operador binario. Lo que la multiplicación es en este contexto es en realidad una forma abreviada de repetir una operación de adición una cierta cantidad de veces.
+
+## Ejemplos de grupos
+
+La mejor manera de tener una idea de un grupo es ver muchos de ellos. Hagámoslo.
+
+### 1. El grupo trivial
+
+Sea nuestro grupo un conjunto formado por el número $\set{0}$ con el operador binario de adición. Está claro que el operador binario es cerrado y asociativo
+
+$$
+(0 + 0) + 0 = (0 + 0) + 0
+$$
+
+y cada elemento tiene una identidad y una inversa.
+
+Este no es un grupo interesante, pero es el más pequeño válido que puedes crear.
+
+Ten en cuenta que un grupo no puede estar vacío porque, por definición, debe contener un elemento identidad.
+
+Como ejercicio para el lector, demuestra que el conjunto $\set{1}$ con el operador binario $\times$ es un grupo.
+
+### 2. Los números reales no son un grupo bajo la multiplicación
+
+Aunque los números reales ($\mathbb{R}$) bajo la multiplicación tienen una identidad (el número 1) y son cerrados y asociativos, no todos tienen una inversa.
+
+Los números reales son invertibles tomando la inversa $(1 / n)$, pero el cero es un número real y no se puede invertir porque $1/0$ no es un número real.
+
+Estrictamente hablando, la inversa de $a$, es $b$ tal que $ab = 1$. Aquí estamos diciendo que si $a = 0$ no hay ningún elemento en el conjunto $b$ tal que $ab = 1$.
+
+Sin embargo, los números reales positivos excluyendo el cero son un grupo bajo la multiplicación. Cada elemento tiene una inversa ($1/n$), y el elemento identidad es 1.
+
+**Ejercicio**: Los números enteros (positivos y negativos) no son un grupo bajo la multiplicación. Muestra cuáles de los cuatro requisitos (cerrado, asociativo, existencia de identidad, todos los elementos tienen una inversa) no se cumplen.
+
+### 3. $n \times m$ matrices de números reales son un grupo bajo la adición
+
+Vamos a resolverlo:
+
+La adición de matrices es cerrada y asociativa. Si sumas una matriz de $n × m$ de números reales con otra matriz de $n × m$ de números reales, obtienes una matriz de $n × m$ de números reales.
+La matriz identidad es una matriz de $n × m$ de todos ceros
+la inversa de una matriz es esa matriz multiplicada por -1.
+Un momento, no se nos permite multiplicar por -1, ¿verdad?
+
+Un grupo no requiere que la inversa sea "computable usando el operador binario de grupo" solo para existir. El grupo de matrices de $n × m$ de números reales contiene inversas para cada elemento, y eso es lo que importa.
+
+Si definimos nuestro operador como el producto de Hadamard (multiplicación elemento por elemento), este no puede ser un grupo por la misma razón que se explicó anteriormente.
+
+Si definimos nuestro operador como la multiplicación tradicional de matrices sobre matrices cuadradas, esto puede ser o no un grupo dependiendo de la definición del conjunto, como veremos en el ejemplo 5 de la sección.
+
+### 4. El conjunto de puntos 2D en un plano euclidiano bajo la adición de elementos es un grupo
+
+En realidad, este es un caso especial del ejemplo anterior, pero veámoslo desde un ángulo diferente.
+
+Consideremos que nuestro conjunto es el conjunto de todos los puntos $(x, y)$ de valor real en un plano 2D típico.
+
+Nuestro operador binario es sumar puntos, por ejemplo $(1,1) + (2,2) = (3,3)$.
+
+Nuestro elemento de identidad es el origen, porque sumar con él dará como resultado la misma ubicación del otro punto.
+
+La inversa es simplemente la "imagen reflejada" sobre el origen (la $x$ y la $y$ invertidas) porque cuando las sumamos, dan como resultado el origen.
+
+### 5. $n \times n$ matrices de determinante distinto de cero bajo multiplicación son un grupo
+
+A modo de repaso, si una matriz tiene un determinante distinto de cero, entonces es invertible. Cuando una matriz de determinante distinto de cero se multiplica por otra matriz de determinante distinto de cero, entonces el producto también tiene un determinante distinto de cero. En realidad, podemos ser más específicos, si $A$, $B$ y $C$ son matrices cuadradas y $AB = C$, entonces $\det(a) \times \det(b) = \det(c)$.
+
+Trabajemos con las definiciones
+
+- La multiplicación de matrices de determinante distinto de cero es cerrada porque no se puede "salir del grupo" ya que el producto siempre tendrá determinante distinto de cero. La multiplicación de matrices es asociativa.
+- El elemento identidad es la matriz identidad (todos ceros, excepto la diagonal principal que es uno).
+- La inversa es simplemente la matriz inversa, y las matrices con determinante distinto de cero son invertibles.
+
+### 6. $n \times n$ matrices con determinante cero bajo multiplicación son un grupo no
+
+Recuerde, una matriz con determinante cero no se puede invertir, por lo que este conjunto no puede tener una inversa. En este caso, no tenemos un elemento identidad porque la matriz identidad tiene determinante uno. Como no tenemos ningún elemento identidad, este conjunto y operador binario ni siquiera es un monoide, es un semigrupo.
+
+### 7. El conjunto de todos los polinomios de un grado fijo acotado superiormente es un grupo bajo adición
+
+Si decimos "todos los polinomios con coeficientes reales de grado 7 como máximo bajo adición", este es un grupo válido.
+
+- La suma de polinomios es cerrada y asociativa
+- La identidad es el polinomio 0 (o $0x^0$ para ser precisos)
+- La inversa son los coeficientes multiplicados por -1
+- No podemos decir que el grado es "exactamente 7" porque el elemento identidad tiene grado 0 y no sería parte del grupo.
+
+Los polinomios de un grado fijo acotado superiormente bajo la multiplicación no son un grupo, porque generalmente el grado aumenta cuando se multiplican polinomios, por lo tanto, el operador no sería cerrado.
+
+### 8. La suma módulo un número primo es un grupo
+
+Tomemos un número primo 7.
+
+Aquí, la identidad sigue siendo 0, porque se suma por 0 y se obtiene el mismo número.
+
+En esta situación, ¿cuál sería la inversa de 5?
+
+Sería simplemente 2, porque 7 - 5 = 2, o 5 + 2 módulo 7 es cero (la identidad).
+
+### 9. La multiplicación módulo de un número primo no es un grupo
+
+El cero no tiene inverso en este ejemplo.
+
+Si omitimos el número 0, entonces tenemos un grupo. El elemento identidad es 1, y el inverso de un elemento $a$ es su inverso modular $a^{-1}$.
+
+### 10. Una base fija elevada a potencias enteras bajo la multiplicación es un grupo
+
+Si se multiplican entre sí dos potencias enteras de $b$, el resultado es la potencia entera del producto de las bases. Por ejemplo, $2^3 \times 2^4 = 2^{3 + 4} = 2^7$. Esto funciona para bases arbitrarias:
+
+$$
+b^x \times b^y = b^{x + y}
+$$
+
+El elemento identidad es $b^0$, que es $1$, y el inverso de $b^x$ es $b^{-x}$.
+
+## Grupos finitos
+
+Como sugiere el nombre, un grupo finito tiene una cantidad finita de elementos. El conjunto de todos los números enteros bajo la adición no es finito, pero la adición de números enteros módulo un número primo es un grupo finito.
+
+En las demostraciones de conocimiento cero, solo usamos grupos finitos.
+
+## Orden de un grupo
+
+El orden de un grupo es la cantidad de elementos que lo componen.
+
+## Grupos cíclicos
+
+Un grupo cíclico es un grupo que tiene un elemento tal que cada elemento del grupo puede ser "generado" aplicando el operador binario repetidamente a ese elemento, o a su inverso.
+
+### Ejemplos de grupos cíclicos
+
+#### Ejemplo 1: El grupo que consiste en 0 bajo la adición es un grupo cíclico
+
+Esto es trivialmente cierto porque 0 + 0 = 0 genera cada elemento del grupo.
+
+#### Ejemplo 2: La suma módulo 7 es un grupo cíclico
+
+Si empezamos con 1 y sumamos 1 a sí mismo repetidamente, generaremos todos los elementos del grupo. Por ejemplo:
+
+$$
+\begin{align*}
+&1 + 1 &= 2 \\
+&1 + 1 + 1 &= 3 \\
+&1 + 1 + 1 + 1 &= 4 \\
+&1 + 1 + 1 + 1 + 1 &= 5 \\
+&1 + 1 + 1 + 1 + 1 + 1 &= 6 \\
+&1 + 1 + 1 + 1 + 1 + 1 &= 0 \\
+&1 + 1 + 1 + 1 + 1 + 1 + 1 &= 1 \\
+\end{align*}
+$$
+
+#### Ejemplo 3: La multiplicación módulo 7 es un grupo cíclico, si excluimos el cero
+
+Debemos tener cuidado al elegir el generador aquí, porque, por ejemplo, 2 no generará todo el grupo.
+
+$$
+\begin{align*}
+&2 * 2 &\equiv 4 \pmod 7 \\
+&2 * 2 * 2 &\equiv 1 \pmod 7 \\
+&2 * 2 * 2 * 2 &\equiv 2 \pmod 7 \\
+&2 * 2 * 2 * 2 * 2 &\equiv 4 \pmod 7 \\
+&...\
+\end{align*}
+$$
+
+Podemos ver que 2 solo puede generar $\set{1,2,4}$. Sin embargo, si elegimos 3 como generador, entonces podemos generar todo el grupo.
+
+$$
+\begin{align*}
+3 ^ 2 \equiv 2 \pmod 7 \\
+3 ^ 3 \equiv 6 \pmod 7 \\
+3 ^ 4 \equiv 4 \pmod 7 \\
+3 ^ 5 \equiv 5 \pmod 7 \\
+3 ^ 6 \equiv 1 \pmod 7 \\
+3 ^ 7 \equiv 3 \pmod 7 \\
+&...\
+\end{align*}
+$$
+
+La razón por la que 3 funciona y 2 no es porque 3 es una *[raíz primitiva](https://en.wikipedia.org/wiki/Primitive_root_modulo_n)*.
+
+Podemos usar la biblioteca Galois para encontrar raíces primitivas:
+
+```python
+from galois import GF
+GF7 = GF(7)
+GF.primitive_elements
+# [3, 5]
+```
+
+### Si un grupo es cíclico, entonces es abeliano
+
+Este es un poco más sutil, pero considere esto:
+
+En un grupo cíclico, cada elemento del grupo puede generarse como $(g + g + … + g)$. Elijamos arbitrariamente un elemento R. Participemos este conjunto de adiciones de la siguiente manera:
+
+$$
+r = \underbrace{g + g + \dots + g}_\text{m veces} + \underbrace{g + g + \dots + g}_\text{n veces}
+$$
+
+Debido a la asociatividad, podemos agregar paréntesis
+
+$$
+r = \underbrace{(g + g + \dots + g)}_\text{m veces} + \underbrace{(g + g + \dots + g)}_\text{n veces}
+$$
+
+Sea $g$ sumado a sí mismo $m$ veces $p$ y $g$ sumado a sí mismo $n$ veces $q$. Por lo tanto,
+
+$$r = p + q$$
+
+Por asociatividad, podemos volver a particionar la ecuación original de la siguiente manera (¡nótese que $m$ y $n$ intercambiaron lugares!)
+
+$$
+R = \underbrace{(g + g + \dots + g)}_\text{n veces} + \underbrace{(g + g + \dots + g)}_\text{m veces}
+$$
+
+Y obtenemos:
+
+$$r = q + p$$
+
+Por lo tanto, si el grupo es cíclico, entonces el grupo es abeliano.
+
+Nótese que el inverso de esta afirmación no es cierto. Los números reales bajo la adición son un grupo abeliano, pero no son cíclicos.
+
+Los grupos cíclicos no tienen que ser aritméticos módulo algún número primo, pero estos son los únicos grupos cíclicos que usaremos en nuestra discusión de las pruebas de conocimiento cero.
+
+## El elemento identidad de un grupo es único
+
+Un grupo no puede tener dos elementos identidad. No pienses demasiado en esto, se deriva por simple contradicción. Digamos que ▢ es nuestro operador binario y $e$ es nuestro elemento identidad.
+
+Digamos que tenemos un elemento identidad alternativo $e'$. Esto significa lo siguiente:
+
+$$a \square a^{-1} = e \text{ and } a \square a^{-1} = e'$$
+
+Si decimos $e≠e'$, entonces también debe ser cierto que
+
+$$a \square a^{-1} \neq a \square a^{-1}$$
+
+Pero eso es obviamente una contradicción, por lo tanto, los elementos identidad deben ser únicos.
+
+## El uso de grupos en las demostraciones de conocimiento cero
+
+Entender la teoría de grupos para el propósito de las demostraciones de conocimiento cero es más un ejercicio de vocabulario. Cuando decimos "inversa" o "identidad" queremos que entiendas inmediatamente lo que significan.
+
+Además, los grupos nos ayudan a razonar sobre objetos matemáticos muy complejos sin entender cómo funcionan. En este artículo hemos utilizado ejemplos conocidos, pero más adelante trataremos objetos muy desconocidos como las *curvas elípticas sobre extensiones de campo*. Aunque no sepas exactamente qué es eso, si te decimos que es un grupo, ya sabes mucho sobre lo que es.
+
+## Aprende más con RareSkills
+
+Este artículo es parte de una serie sobre ZK Proofs. Consulta nuestro [Libro ZK](https://www.rareskills.io/zk-book) para ver la serie completa.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/homomorphisms_es.md b/spanish-es/homomorphisms_es.md
new file mode 100644
index 0000000..df3a018
--- /dev/null
+++ b/spanish-es/homomorphisms_es.md
@@ -0,0 +1,280 @@
+# Homomorfismos por ejemplo
+
+Existe un homomorfismo entre dos grupos si existe una *mapa que preserva la estructura* entre los dos grupos.
+
+Supongamos que tenemos dos estructuras de datos algebraicos $(A,\square)$ y $(B, \blacksquare)$, donde el operador binario de $A$ es $\square$ y el operador binario de $B$ es $\blacksquare$.
+
+Existe un homomorfismo de $A$ a $B$ si y solo si existe una función $\phi: A\rightarrow B$ tal que
+
+$$
+\phi(a_i \square a_j)=\phi(a_i)\blacksquare\phi(a_j)\space\space\forall a_i,a_j\in A
+$$
+
+En otras palabras, si $a_i \square a_j = a_k$, entonces $\phi(a_i) \blacksquare \phi(a_j) = \phi(a_k)$.
+
+Tenga en cuenta que un homomorfismo es unidireccional. La función $\phi$ toma elementos en $A$ y los asigna a elementos en $B$. No tenemos requisitos sobre "ir hacia atrás".
+
+Primero mostraremos algunos ejemplos simples, proporcionaremos algunas aclaraciones y luego proporcionaremos ejemplos más complejos.
+
+## Ejemplos simples de homomorfismos
+
+### Todos los números enteros bajo adición a todos los números enteros pares bajo adición
+
+Sea $A$ el conjunto de todos los números enteros bajo adición y sea $B$ el conjunto de todos los números enteros pares bajo adición. Está claro que tanto $A$ como $B$ son grupos.
+
+Sea $\phi(x)=2x$
+
+Vemos que $\phi$ define un homomorfismo de $A$ a $B$ porque lo siguiente es cierto para cualquier par de enteros $a_i$ y $a_j$
+
+$$
+\begin{align*}
+\phi(a_i+a_j)&=\phi(a_i)+\phi(a_j)\\
+2(a_i+a_j)&=2(a_i)+2(a_j)
+\end{align*}
+$$
+
+### Todas las cadenas bajo concatenación a todos los enteros cero o mayores
+
+Por ejemplo, sea $A$ el Monoide de todas las cadenas (incluida la cadena vacía) bajo concatenación, y sea $B$ el Monoide de todos los enteros cero o mayores bajo adición.
+
+Existe un homomorfismo de $A$ a $B$ porque existe una función $\phi$ que asigna cadenas a números enteros mayores o iguales a cero y conserva la siguiente propiedad
+
+$$
+\phi(a_i+a_j)=\phi(a_i)+\phi(a_j)
+$$
+
+En este caso, $\phi$ es la *longitud* de la cadena. Por ejemplo:
+
+$$
+\begin{align*}
+\text{Raro}&\rightarrow 4\\
+\text{Habilidades}&\rightarrow 6\\
+\text{HabilidadesRaras}&\rightarrow 10\\
+\end{align*}
+$$
+
+Aquí tenemos
+
+$$
+\begin{align*}
+\phi(\text{Raro})&=4\\
+\phi(\text{Habilidades})&=6\\
+\phi(\text{HabilidadesRaras})&=10\\
+\phi(\mathsf{concat}(\text{Raro},\text{Habilidades}))&=\phi(\text{Raro})+\phi(\text{Habilidades})\\
+\end{align*}
+$$
+
+### Todos los números reales bajo suma a todas las matrices $n\times m$ de números reales bajo suma
+
+Algunas Los homomorfismos pueden parecer bastante triviales una vez que se les toma la mano. Este es un ejemplo de un homomorfismo de este tipo. En este caso, nuestra función $\phi$ simplemente repite el número real $n\times m$ veces. Por ejemplo, si $n=3$ y $m=2$, entonces $\phi(8.8)$ sería:
+
+$$
+\begin{bmatrix}
+8.8&8.8\\
+8.8&8.8\\
+8.8&8.8
+\end{bmatrix}
+$$
+
+Por ejemplo, si $\phi(8.8 + 0.2)=\phi(8.8)+\phi(0.2)$ porque
+
+$$
+\begin{bmatrix}
+9&9\\
+9&9\\
+9&9\\
+\end{bmatrix}=
+\begin{bmatrix}
+8.8&8.8\\
+8.8&8.8\\
+8.8&8.8
+\end{bmatrix}+
+\begin{bmatrix}
+0.2&0.2\\
+0.2&0.2\\
+0.2&0.2\\
+\end{bmatrix}
+$$
+
+## Aclaraciones sobre homomorfismos
+
+- $\phi$ debe funcionar con cada par posible de elementos de $A$ (incluidos pares del mismo elemento). Sin embargo, no necesita “acceder” a todos los elementos de $B$. Por ejemplo, un homomorfismo que mapea cada elemento en $A$ al elemento identidad en $B$ es un homomorfismo válido, pero no útil. Se llama *homomorfismo trivial*.
+- Si elegimos dos conjuntos arbitrarios con un operador binario, no necesariamente existe un homomorfismo.
+- Puede haber un homomorfismo de $A$ a $B$, pero no necesariamente de $B$ a $A$.
+- Si existe un homomorfismo de $A$ a $B$ y de $B$ a $A$, y $\phi$ es la función de $A$ a $B$, la inversa de $\phi$ puede no ser necesariamente una función válida para el homomorfismo de $B$ a $A$
+
+## Más ejemplos de homomorfismos
+
+### Números enteros bajo la adición a potencias enteras de $b$ bajo la multiplicación
+
+Supongamos que tenemos el grupo $A=(\mathbb{Z},+)$ (el conjunto de todos los números enteros bajo la adición) y el grupo $B$, que es el conjunto de todas las potencias enteras de $b$ bajo la multiplicación, es decir, $B=(b^i\space:\space i\in\mathbb{Z}, \times)$. Podemos fijar arbitrariamente $b=2$ para que el ejemplo sea más fácil de entender.
+
+Existe un homomorfismo de $A$ a $B$, definido por $\phi(x)=b^x$. Según las reglas del álgebra,
+
+$$
+\begin{align*}
+\phi(a_i+a_j)&=\phi(a_i)\times\phi(a_j)\\
+b^{a_i + a_j}&=b^{a_i}b^{a_j}
+\end{align*}
+$$
+
+Para entender por qué se cumple esta relación, considere que
+
+$$
+b^{a_i}=\underbrace{b\cdot b\cdot\dots\cdot b}_{{a_i} \text{ veces}}
+$$
+
+$$
+b^{a_j}=\underbrace{b\cdot b\cdot\dots\cdot b}_{{a_j} \text{ veces}}
+$$
+
+$$
+b^{a_i +a_j}=\underbrace{b\cdot b\cdot\dots\cdot b}_{{a_i} \text{ veces}}\cdot\underbrace{b\cdot b\cdot\puntos\cdot b}_{{a_j} \text{ veces}}
+$$
+
+$$
+b^{a_i +a_j}=\underbrace{b\cdot b\cdot\dots\cdot b\cdot b\cdot b\dots\cdot b}_{{a_i+a_j} \text{ veces}}
+$$
+
+### Números enteros bajo la suma de potencias enteras de $b$ bajo la multiplicación módulo un número primo
+
+### Matrices de $n\times m$ bajo la suma de números enteros bajo la suma
+
+En este caso, $\phi$ simplemente suma todos los elementos de una matriz. Por qué esto funciona se deja como ejercicio para el lector.
+
+### Matrices de $2\times2$ números enteros bajo la multiplicación a números enteros bajo la multiplicación
+
+Hay un homomorfismo del primer al segundo Monoide porque $\phi$ es el *determinante* de la matriz y se cumple la siguiente regla:
+
+$$
+XY=Z\rightarrow\det(X)\det(Y)=\det(Z)
+$$
+
+donde $X,Y,Z$ son matrices de números enteros de $2\times2$. Por qué estas dos estructuras de datos algebraicos son Monoides y no grupos se deja como ejercicio para el lector.
+
+### El grupo de los números racionales (excluidos los números racionales cuyo denominador es un múltiplo de $p$) a la suma módulo $p$
+
+Este concepto ya se enseñó en nuestro artículo sobre [campos finitos](https://www.rareskills.io/post/finite-fields), pero no usamos el término “homomorfismo” para describirlo.
+
+Sea $A$ el grupo de todos los números racionales cuyos denominadores no son múltiplos de $p$, bajo la suma. Sea $B$ el cuerpo finito módulo $p$.
+
+Existe un homomorfismo del grupo $A$ al grupo $B$. $\phi$ es
+
+$$
+\phi(x) = \mathsf{numerador}(x)\times\mathsf{modular\_inverse}(\mathsf{denominador}(x)) \pmod p
+$$
+
+O en Python:
+
+```python
+p = 11
+def phi(num, den):
+ return num * pow(den, -1, p) % p
+```
+
+Por ejemplo:
+
+- $1/3 + 3/5 = 14/15$
+- $1/3$ es congruente con $6 \pmod {17}$
+- $3/5$ es congruente con $4 \pmod {17}$
+- $4 + 6\equiv10 \pmod {17}$
+- $14/15\equiv 10 \pmod {17}$
+
+Decir que $1/3$ es congruente con $6 \pmod {17}$ es equivalente a la afirmación $\phi(1/3)=6$.
+
+### El Monoide de los números racionales (excluyendo los números racionales donde el denominador es un múltiplo de $p$) a la multiplicación módulo $p$ (excluyendo cero)
+
+Usemos el mismo ejemplo que el anterior, pero con multiplicación. La función $\phi$ sigue siendo la misma.
+
+- $1/3 * 3/5 = 1/5$
+- $1/3$ es congruente con $6 \pmod {17}$
+- $3/5$ es congruente con $4 \pmod {17}$
+- $4 \times 6\equiv7 \pmod {17}$
+- $1/5\equiv 7 \pmod {17}$
+
+## Ejercicios para el lector
+
+Encuentre un homomorfismo para los siguientes pares de estructuras de datos algebraicos. Si te quedas atascado (o simplemente no quieres resolver el problema), puedes buscar la respuesta en Google o consultar con un chatbot.
+
+1. Números reales bajo adición a polinomios con coeficientes reales bajo adición.
+2. Polinomios con coeficientes reales a números reales bajo adición. Pista: aunque esto parezca similar al problema 1, la función $\phi$ no tendrá ninguna relación con la respuesta del problema anterior.
+3. Números reales positivos mayores que cero bajo multiplicación a todos los números reales bajo adición.
+
+## Cifrado homomórfico
+
+Si $\phi$ es computacionalmente difícil de invertir, entonces $\phi$ *cifra homomórficamente* los elementos de $A$.
+
+Sea $A$ todos los números enteros bajo adición, y $B$ el grupo objetivo y $\blacksquare$ el operador binario de $B$.
+
+### Adición con conocimiento cero, ejemplo 1
+Supongamos que queremos demostrarle a un verificador que calculamos $2 + 3=5$. Le daríamos al verificador $(x, y, 5)$ donde $x=\phi(2), y= \phi(3)$ y el verificador verificaría que:
+
+$$
+x\blacksquare y \stackrel{?}=\phi(5)
+$$
+
+Tenga en cuenta que el cifrado homomórfico implica que el verificador conoce la función $\phi$.
+
+### Adición con conocimiento cero, ejemplo 2
+Un probador afirma: "Tengo dos números $a$ y $b$, y $b$ es cinco veces $a$". El probador envía $\phi(a)$ y $\phi(b)$ al verificador, y el verificador verifica que
+
+$$\phi(a) + \phi(a) + \phi(a) + \phi(a) + \phi(a) = \phi(b)$$
+
+Recuerde, "multiplicación" aquí no es el operador binario, es simplemente una forma abreviada de suma repetida.
+
+En estos ejemplos, tenga en cuenta que no dijimos nada sobre qué son los elementos de $B$ o qué es $\blacksquare$. $B$ pueden ser objetos matemáticos aterradores, y $\blacksquare$ puede ser un operador matemático aterrador, pero *eso no importa*.
+
+Esta es la belleza del álgebra abstracta: *no necesitamos saberlo*. Mientras tenga las propiedades que nos interesan, podemos razonar sobre su comportamiento incluso si no sabemos nada sobre la implementación.
+
+## Motivación
+
+Bien, genial; entendemos los grupos y los homomorfismos, pero ¿cómo nos ayuda esto? La razón por la que me tomé todo el esfuerzo de explicar esto es porque quiero que entiendas la siguiente afirmación:
+
+“Los puntos de la curva elíptica en un cuerpo finito bajo la adición son un grupo cíclico finito y los números enteros bajo la adición son homomórficos a este grupo”.
+
+Probablemente no sepas qué son los puntos de la curva elíptica o qué significa sumarlos, pero sí sabes:
+
+1. El conjunto de puntos de la curva elíptica bajo la adición produce otro punto de la curva elíptica.
+2. El operador binario que toma dos puntos de la curva elíptica y devuelve otro punto de la curva elíptica es asociativo.
+3. El conjunto de puntos de la curva elíptica contiene un elemento identidad.
+4. El grupo de la curva elíptica tiene un elemento identidad, que es único.
+5. Cada punto de la curva elíptica tiene una inversa, de modo que sumar un punto y su inversa produce la identidad.
+6. Debido a que el grupo es cíclico, cada punto de la curva elíptica se puede generar aplicando repetidamente el operador binario a algún elemento generador.
+7. Debido a que el grupo de puntos de la curva elíptica es cíclico, también es un grupo abeliano.
+8. Debido a que es un grupo finito, el orden es finito.
+9. Debido al homomorfismo, tenemos una idea clara de cómo se comporta el operador binario para los puntos de la curva elíptica. Podemos usar el operador binario de punto de la curva elíptica para "sumar números enteros" en cierto sentido.
+
+Aunque no sepas qué son los puntos de la curva elíptica, ¡ya sabes nueve cosas sobre ellos!
+
+Así que, sean lo que sean estos extraños objetos "puntos de la curva elíptica", sabes que se comportan como los grupos que analizamos anteriormente y que tienen las mismas propiedades.
+
+Lo creas o no, ya has recorrido el 90 % del camino para comprender las curvas elípticas. Es mucho más fácil entender las curvas elípticas si se entiende su similitud con otras estructuras conocidas que si se intenta comprender su matemática extraña desde el principio.
+
+Esto es similar a que yo te diga que Ethereum utiliza "árboles Patricia Merkle" para almacenar el estado. Puede que no sepas qué es un "árbol Patricia" o un "árbol Merkle", pero sí sabes:
+
+- Tiene una raíz.
+- Probablemente puedas acceder a los elementos en tiempo logarítmico, o al menos esa es la intención.
+- Algo útil se almacena en las hojas.
+- Existe algún algoritmo para recorrer el árbol y acceder a una hoja que te interese.
+
+Por lo tanto, cuando te digo que los puntos de la curva elíptica bajo la suma forman un grupo, ya deberías saber qué buscar cuando aprendas sobre ese tema.
+
+Una vez más, los grupos no necesitan ser matemáticas lunares misteriosas. Has trabajado con grupos intuitivamente como programador. Ahora tienes una palabra concreta para describir este fenómeno recurrente.
+
+Es mucho más eficiente decir "grupo" que decir "este es un conjunto con una forma de combinar elementos asociativamente y todos los elementos tienen bla, bla, bla".
+
+Sé que esto puede parecer una gran digresión, pero créanme, comprender el "homomorfismo" nos permite describir de manera sucinta un concepto que veremos con regularidad. También será útil nuevamente cuando discutamos [Programas aritméticos cuadráticos](https://www.rareskills.io/post/quadratic-arithmetic-program). Los homomorfismos aparecen con frecuencia en el mundo de ZK.
+
+Imagínense intentar discutir estructuras de datos de árboles sin una palabra para "raíces" u "hojas". Eso sería inmensamente frustrante.
+
+## Resumen
+
+Existe un homomorfismo de $A$ a $B$ **si y solo si** existe una función $\phi$ que toma un elemento de $A$ y devuelve un elemento de $B$ y $\phi(a_i \square a_j)=\phi(a_i)\blacksquare\phi(a_j)$ o todos los $a_i$ y $a_j$ en $A$, donde $\square$ es el operador binario de $A$ y $\blacksquare$ es el operador binario de $B$. **La existencia de $\phi$ es suficiente para que exista el homomorfismo.**
+
+Los homomorfismos no son necesariamente bidireccionales. Solo se requiere que funcionen en una dirección, de $A$ a $B$.
+
+Si $\phi: A \rightarrow B$ es computacionalmente difícil de invertir, entonces $\phi$ encripta homomórficamente los elementos de $A$. Eso significa que podemos validar afirmaciones sobre cálculos en $A$ usando elementos en $B$.
+
+La buena noticia es que hemos terminado con nuestro tratamiento del álgebra abstracta y ahora tenemos una base sólida para pasar a las [curvas elípticas](https://www.rareskills.io/post/elliptic-curve-addition).
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/p-vs-np_es.md b/spanish-es/p-vs-np_es.md
new file mode 100644
index 0000000..8ed624f
--- /dev/null
+++ b/spanish-es/p-vs-np_es.md
@@ -0,0 +1,521 @@
+# P vs NP y su aplicación a las pruebas de conocimiento cero
+
+El problema P = NP plantea la siguiente pregunta: "Si podemos verificar rápidamente que la solución de un problema es correcta, ¿podemos también calcular rápidamente la solución?" La mayoría de los investigadores creen que la respuesta es no, es decir, P ≠ NP.
+
+Al comprender el problema P vs NP, podemos ver cómo las Zero Knowledge Proofs (ZKPs) encajan en el campo más amplio de la informática y comprender lo que las ZKP pueden y no pueden hacer.
+
+Es mucho más fácil "entender" las pruebas de conocimiento cero relacionándolas con el problema P vs NP.
+
+Este tutorial tiene tres partes:
+1. Explicación del problema P vs NP
+2. Expresar problemas y soluciones como una fórmula booleana
+3. P vs NP y cómo se relacionan con las pruebas de conocimiento cero
+
+## Requisitos previos
+Suponemos que el lector está familiarizado con la complejidad temporal y la notación $\mathcal{O}$ mayúscula.
+
+Decimos que un algoritmo tarda un tiempo polinomial si se ejecuta en un tiempo de $\mathcal{O}(nᶜ)$ o más rápido, donde $n$ es el tamaño de la entrada y $c$ es una constante no negativa. Podemos referirnos a los algoritmos que se ejecutan en un tiempo polinomial o más rápido como *algoritmos eficientes* porque su tiempo de ejecución no crece demasiado rápido con el tamaño de la entrada.
+
+Decimos que un algoritmo tarda *tiempo exponencial* o es *costoso* si se ejecuta en $\mathcal{O}(cⁿ)$ donde $c$ es una constante mayor que 1 y $n$ es el tamaño de la entrada porque el algoritmo se vuelve exponencialmente lento a medida que aumenta el tamaño de la entrada.
+
+## Parte 1: Explicación del problema P vs NP
+### Los problemas en P son problemas que son fáciles de resolver y fáciles de verificar sus soluciones.
+
+Los problemas que se pueden resolver en tiempo polinómico y cuyas soluciones se pueden verificar en tiempo polinómico se denominan problemas en P.
+
+A continuación se muestran algunos ejemplos de problemas cuyas soluciones son fáciles de calcular y verificar. Estas tareas pueden ser realizadas por diferentes partes, una que realiza el cálculo y otra que verifica que los resultados sean válidos:
+
+#### Ejemplo 1 de P: Ordenar una lista
+Podemos ordenar una lista de manera eficiente y podemos verificar de manera eficiente que una lista esté ordenada.
+- **Resolución:** Ordenar la lista requiere $\mathcal{O}(n \log n)$ tiempo (por ejemplo, utilizando mergesort), que es tiempo polinómico. Aunque $n \log n$ no es un polinomio, sabemos que $\log n < n$ y, por lo tanto, $(n \log n) < n²$, por lo que el tiempo de ejecución de nuestro algoritmo está limitado por encima de algún polinomio, que es el requisito para el "tiempo polinómico".
+
+- **Verificación:** Podemos verificar que la lista esté ordenada recorriéndola y comprobando que cada elemento sea mayor que su vecino izquierdo, lo que llevaría $\mathcal{O}(n)$ tiempo.
+
+#### Ejemplo 2 de P: Devolver el índice de un número en una lista, si aparece en la lista
+Podemos buscar de manera eficiente para ver si un número está en una lista y luego verificar de manera aún más eficiente que el número esté presente si conocemos el índice en el que está.
+
+- **Resolución:** Por ejemplo, dada la lista `[8, 2, 1, 6, 7, 3]`, necesitamos $\mathcal{O}(n)$ tiempo para determinar si el número `7` está en la lista.
+
+- **Verificación:** Pero si le damos la lista y decimos que 7 está en el índice 4, puede verificar que el número esté en la lista en esa posición en $\mathcal{O}(1)$ tiempo. Buscar un elemento, si no nos dicen su posición, toma $\mathcal{O}(n)$ tiempo en el caso general, ya que tenemos que buscar en la lista. Si nos dicen la supuesta ubicación del elemento, toma $\mathcal{O}(1)$ tiempo verificar que el elemento está, de hecho, en la lista en esa ubicación.
+
+#### Ejemplo 3 de P: Determinar si dos nodos en un gráfico están conectados
+Podemos determinar de manera eficiente si dos nodos en un gráfico están conectados usando una búsqueda en amplitud: comenzar en un nodo, luego visitar todos sus vecinos excepto los nodos que ya hemos visitado, luego buscar los vecinos de los vecinos, y así sucesivamente.
+
+- **Resolución:** Descubrir la ruta entre nodos usando una búsqueda en amplitud tomará $\mathcal{O}(n + e)$ tiempo, donde $n$ es el número de nodos en el gráfico y $e$ es el número de aristas. El número de aristas $e$ no puede ser mayor que $n^2$, por lo que podemos tratar a $\mathcal{O}(n + e)$ como $\mathcal{O}(n²)$ en el peor de los casos.
+
+- **Verificación:** Podemos verificar que la ruta propuesta sea válida en tiempo $\mathcal{O}(n)$ simplemente siguiendo la ruta propuesta para ver si los dos puntos realmente están conectados por esa ruta.
+
+**En todos los ejemplos anteriores, tanto el cálculo como la verificación de la solución se pueden realizar en tiempo polinomial.**
+
+#### El testigo
+Un *testigo* en informática es una prueba de que resolviste el problema correctamente. En los ejemplos anteriores, el testigo es la respuesta correcta al problema. Para los ejemplos anteriores, estas son las cosas que podríamos usar como testigo:
+1. La lista ordenada
+2. El índice donde aparece un número en la lista
+3. La ruta entre dos nodos en un gráfico
+
+Veremos más adelante que un testigo no necesariamente tiene que ser la solución al problema original. También podría ser una solución para una representación alternativa del mismo problema.
+
+### Problemas en PSPACE: No todos los problemas tienen soluciones que se puedan verificar de manera eficiente
+Los problemas que requieren recursos exponenciales para resolverse y verificarse se denominan problemas en PSPACE. La razón por la que se denominan PSPACE es que, aunque pueden requerir un tiempo exponencial para resolverse, no necesariamente requieren un espacio de memoria exponencial para ejecutar la búsqueda.
+
+Esta clase de problemas se ha investigado ampliamente, pero no se ha descubierto ningún algoritmo eficiente para resolverlos. Muchos investigadores creen que no existe ningún algoritmo eficiente para resolver estos problemas. Si se pudiera descubrir una solución eficiente a estos problemas, también sería posible reutilizar el algoritmo para romper todos los cifrados modernos y alterar fundamentalmente la informática tal como la conocemos.
+
+A pesar de los incentivos significativos para encontrar soluciones eficientes a estos problemas, la evidencia sugiere que es probable que tales soluciones no existan. Estos problemas son tan desafiantes que no se pueden proporcionar pruebas fácilmente verificables (testigos) incluso si se resuelven correctamente.
+
+#### Ejemplos de problemas en PSPACE
+##### Ejemplo 1 de PSPACE: Encontrar el movimiento óptimo en ajedrez
+
+
+Supongamos que le preguntamos a una computadora poderosa: "Dado este tablero de ajedrez con las piezas en esta posición, ¿cuál es el próximo movimiento óptimo?"
+
+La computadora responde "mueva el peón negro en f4 a f3".
+
+¿Cómo puede confiar en que la computadora le está dando la respuesta correcta?
+
+No hay una manera eficiente de comprobarlo; hay que hacer el mismo trabajo que hizo la computadora. Esto implica hacer una búsqueda completa a través de todos los posibles estados futuros del tablero. No hay ningún testigo que la computadora pueda proporcionarnos que nos permita confirmar que "mover el peón negro en f4 a f3" es en realidad el siguiente mejor movimiento. De esta manera, la naturaleza de este problema es muy diferente de los ejemplos discutidos anteriormente: no podemos verificar de manera eficiente que el movimiento óptimo declarado sea el verdadero movimiento óptimo.
+
+En este ejemplo, el "testigo" presentado por la computadora consiste en todos los posibles estados futuros del juego. Sin embargo, el volumen masivo de estos datos hace que sea prácticamente imposible verificar la precisión de la solución de manera eficiente.
+
+##### Ejemplo 2 de PSPACE: Determinar si las expresiones regulares son equivalentes
+Las dos expresiones regulares, `a+` y `aa*`, coinciden con las mismas cadenas. Si una cadena coincide con la primera expresión regular, también coincidirá con la segunda, y viceversa.
+
+Sin embargo, comprobar si dos expresiones regulares *arbitrarias* son equivalentes requiere un tiempo de cálculo exponencial. Incluso si una computadora potente le dijera que coinciden con las mismas cadenas, no hay una prueba breve (testigo) que la computadora pueda darle para demostrar que las respuestas son correctas. De manera similar al ejemplo del ajedrez, tendría que buscar en un espacio muy grande de cadenas para comprobar si las expresiones regulares son equivalentes, y eso tomará un tiempo exponencial.
+
+Tanto el ajedrez como la equivalencia de expresiones regulares tienen una característica común: ambos requieren recursos exponenciales para encontrar respuestas y recursos exponenciales para verificar las respuestas.
+
+#### Problemas que requieren un uso computacional aún más intensivo que PSPACE
+Hay problemas que son tan difíciles que requieren un tiempo exponencial y una memoria exponencial para resolverlos, pero esos problemas suelen ser teóricos y no aparecen con frecuencia en el mundo real.
+
+Un ejemplo de este tipo de problema son las damas, con una regla según la cual las piezas nunca pueden moverse a una posición que recree un estado anterior del tablero. Para asegurarnos de no repetir un estado del tablero en un juego mientras exploramos el espacio de posibles movimientos, tenemos que llevar un registro de todos los estados del tablero que ya se han visitado. Dado que la duración del juego puede ser exponencial en el tamaño del tablero, los requisitos de memoria también son exponenciales.
+
+### Problemas en NP: Algunos problemas se pueden verificar rápidamente, pero no calcular rápidamente
+Si podemos verificar rápidamente la solución de un problema, entonces el problema es en NP. Sin embargo, encontrar la solución puede requerir recursos exponenciales.
+
+Cualquier problema cuya solución propuesta (testigo) se pueda verificar rápidamente como correcta es un problema NP. Si el problema también tiene un algoritmo para encontrar la solución en tiempo polinomial, entonces es un problema P. Todos los problemas P son problemas NP, pero es extremadamente improbable que todos los problemas NP también sean problemas P.
+
+Ejemplos de problemas en NP. Estos se explican con más detalle a continuación:
+- Calcular la solución de un sudoku: verificar la solución propuesta para un sudoku.
+- Calcular la tricoloración de un mapa (si existe): verificar una tricoloración propuesta de un mapa.
+- Encontrar una asignación a una fórmula booleana que dé como resultado verdadero: verificar la asignación propuesta hace que la fórmula dé como resultado verdadero.
+
+**Nota:** NP significa polinomio no determinista. No entraremos en la jerga sobre el origen de ese nombre; solo damos el nombre para que el lector no piense erróneamente que significa "tiempo no polinomial".
+
+#### Ejemplos de problemas en NP
+##### Ejemplo 1 de NP: Sudoku
+En el juego Sudoku, se le da a un jugador una cuadrícula de $9 \times 9$ con algunos números completos. El objetivo es que el jugador complete el resto de la cuadrícula con los números del 1 al 9 de manera que ningún número aparezca más de una vez en cualquier fila, columna o casilla de $3 \times 3$ (las que están delineadas con líneas en negrita). Las siguientes imágenes de [Wikipedia](https://en.wikipedia.org/wiki/Sudoku) ilustran esto. En la primera imagen, vemos la cuadrícula de 9x9 tal como se le da al jugador. En la segunda imagen, vemos la solución del jugador.
+
+
+
+
+
+Dada una *solución* de un sudoku, podemos verificar rápidamente que la solución es correcta simplemente recorriendo las columnas, filas y subcuadrículas de $3\times 3$. El testigo puede verificarse en tiempo polinomial.
+
+Sin embargo, *calcular* la solución requiere significativamente más recursos: hay una cantidad exponencial de combinaciones para buscar. Para una cuadrícula de $9\times 9$, esto no es difícil para una computadora. Sin embargo, si permitimos que el sudoku sea arbitrariamente grande: cada lado tiene un tamaño $n$, donde $n$ es un múltiplo de 9. En ese caso, la dificultad de encontrar la solución crece exponencialmente con $n$.
+
+##### Ejemplo 2 de NP: Tricoloración de un mapa
+Cualquier mapa 2D de territorios puede ser “coloreado” con solo cuatro colores (ver el [teorema de los cuatro colores](https://en.wikipedia.org/wiki/Four_color_theorem)). Es decir, podemos asignar un color único (uno de los cuatro colores) a cada territorio de modo que ningún territorio vecino comparta el mismo color. Por ejemplo, la siguiente imagen (de [Wikipedia](https://en.wikipedia.org/wiki/U.S._state#/media/File:Map_of_USA_with_state_names_2.svg)) muestra los Estados Unidos coloreados con cuatro colores: rosa, verde, amarillo y rojo. Tómese un momento para observar la verificación de que no se ha asignado el mismo color a dos estados en contacto:
+
+
+
+El problema de los tres colores pregunta si un mapa se puede colorear usando solo tres colores en lugar de cuatro. Descubrir un tricolor (si existe) es un problema de búsqueda que requiere un uso intensivo de recursos computacionales. Sin embargo, verificar una *propuesta* de 3 colores es fácil: recorra cada una de las regiones y verifique que ninguna región vecina tenga el mismo color que el territorio que se está verificando actualmente.
+
+Resulta que no es posible aplicar 3 colores a los Estados Unidos.
+
+Las razones por las que un mapa en particular no puede tener 3 colores varían, pero en el caso de los Estados Unidos, Nevada (la región roja en el mapa a continuación) está rodeada por cinco territorios. Coloreamos Nevada con un color, luego debemos alternar los colores de sus territorios vecinos. Sin embargo, cuando terminemos de rodear a los vecinos de Nevada, terminaremos con un territorio que tiene vecinos con tres colores en sus límites, lo que no deja ningún color válido para el territorio sin colorear.
+
+
+
+Aquí hay un [video rápido e interesante sobre mapas de 3 colores](https://www.youtube.com/watch?v=WlcXoz6tn4g) si desea obtener más información sobre este problema.
+
+Sin embargo, es posible aplicar tres colores a Australia:
+
+
+
+No todos los mapas pueden tener tres colores. Calcular un tricolor para un mapa 2D arbitrario, si existe, no se puede hacer de manera eficiente; por lo general, se requiere una búsqueda de fuerza bruta que puede llevar un tiempo exponencial.
+
+Sin embargo, si alguien resuelve un tricolor, es fácil verificar su solución.
+
+### La relación entre P, NP y PSPACE
+#### Recursos computacionales para cada clase
+La siguiente tabla resume los recursos computacionales necesarios para cada clase de problema:
+
+| Categoría | Tiempo de cálculo | Tiempo de verificación |
+| --- | --- | --- |
+| P | Debe ser polinomial o mejor | Debe ser polinomial o mejor
+| NP | Sin requisitos | Debe ser polinomial o mejor |
+| PSPACE | Sin requisitos | Sin requisitos |
+
+#### Jerarquía de dificultad entre P, NP y PSPACE
+Cualquier problema que requiera recursos exponenciales para verificar el testigo es un PSPACE (o un problema más difícil). Si una persona tiene recursos exponenciales para verificar testigos para problemas PSPACE, puede calcular de manera trivial soluciones para cualquier problema P o NP. Por lo tanto, todos los problemas P y NP son un subconjunto de los problemas PSPACE, como se ilustra en la siguiente figura.
+
+En otras palabras, si tienes una computadora lo suficientemente potente para resolver o verificar una clase de problema en el círculo más grande, puedes resolver o verificar un subconjunto de él:
+
+
+
+### El problema P vs. NP
+P es la clase de problemas que se pueden resolver y verificar de manera eficiente, mientras que NP es la clase de problemas que se pueden verificar de manera eficiente. La pregunta "P vs NP" pregunta, simplemente, si estas dos clases son la misma.
+
+Si P = NP, significaría que siempre que podemos encontrar un método eficiente para verificar una solución, también podemos encontrar un método eficiente para encontrar esa solución. Recuerde que encontrar una solución es siempre al menos tan difícil como verificarla. (Por definición, resolver un problema incluye encontrar la respuesta correcta, lo que significa que un algoritmo que resuelve el problema también verifica su respuesta en el proceso).
+
+Si P = NP es cierto, eso significa que hay un algoritmo eficiente para calcular sudokus (de tamaño arbitrario) y encontrar si existe un color triple. También significa que hay un algoritmo eficiente para descifrar la mayoría de los algoritmos criptográficos modernos.
+
+Actualmente, sigue sin demostrarse si P y NP son el mismo conjunto. Aunque se han hecho numerosos intentos para encontrar algoritmos eficientes para problemas NP, toda la evidencia sugiere que tales algoritmos no existen.
+
+De manera similar, sigue sin saberse si existen soluciones eficientes o mecanismos de verificación para los problemas PSPACE. Aunque los investigadores especulan ampliamente que P ≠ NP y NP ≠ PSPACE, no existe ninguna prueba matemática formal de estas conclusiones. Por lo tanto, a pesar de los grandes esfuerzos, siguen sin descubrirse soluciones eficientes para los problemas NP y métodos de verificación eficientes para los problemas PSPACE.
+
+Para fines prácticos, podemos suponer que P ≠ NP y NP ≠ PSPACE. De hecho, hacemos esa suposición implícitamente cuando confiamos datos importantes a algoritmos criptográficos modernos.
+
+## Parte 2: Expresar problemas y soluciones como fórmulas booleanas
+Lo que une a los problemas P y NP es que su solución se puede verificar rápidamente. Sería extremadamente útil si pudiéramos describir todos esos problemas (P y NP) y sus soluciones en un lenguaje común. Es decir, queremos una codificación del problema que funcione para problemas tan diversos como probar que una lista está ordenada, probar que un sudoku está resuelto o probar que tenemos un colorante de tres.
+
+**La verificación de una solución a un problema en NP o P se puede lograr verificando una solución a una fórmula booleana que modela el problema.**
+
+Lo que queremos decir con "una fórmula booleana que modela el problema" quedará claro a medida que describamos lo que queremos decir con "una solución a una fórmula booleana" y observemos algunos ejemplos de modelado de problemas con fórmulas booleanas.
+
+### Soluciones a una fórmula booleana
+Para expresar una fórmula booleana, utilizamos el operador $¬$ para representar el NO booleano, $∧$ para representar el AND booleano y $∨$ para representar el OR booleano. Por ejemplo, $a ∧ b$ se evalúa como verdadero si y solo si $a$ y $b$ son ambos verdaderos. $a ∧ ¬b$ se evalúa como verdadero si y solo si $a$ es verdadero y $b$ es falso.
+
+Supongamos que tenemos un conjunto de variables booleanas $x₁$, $x₂$, $x₃$, $x₄$ y una fórmula booleana:
+
+$$
+out = (x₁ ∨ ¬x₂ ∨ ¬ x₃) ∧ (¬x₂ ∨ x₃ ∨ x₄) ∧ (x₁ ∨ x₃ ∨ ¬x₄) ∧ (¬x₂ ∨ ¬x₃∨ ¬x₄)
+$$
+
+La pregunta es: ¿podemos encontrar valores para $x₁, x₂, x₃, x₄$ tales que $out$ sea verdadero? Para la fórmula anterior, podemos. Escribiendo $T$ para verdadero y $F$ para falso, podemos escribir nuestra solución como:
+
+$$
+\begin{align*}
+x₁ = T \\
+x₂ = F \\
+x₃ = T \\
+x₄ = F
+\end{align*}
+$$
+
+Sustituyendo la solución en la fórmula obtenemos:
+
+$$
+\begin{align*}
+x₁ &= T \\
+x₂ &= F \\
+x₃ &= T \\
+x₄ &= F \\
+out &= (x₁ ∨ ¬x₂ ∨ ¬ x₃) ∧ (¬x₂ ∨ x₃ ∨ x₄) ∧
+ (x₁ ∨ x₃ ∨ ¬x₄)∧ (¬x₂ ∨ ¬x₃∨ ¬x₄) \\
+out &= (T ∨ ¬ F ∨ ¬ T) ∧ (¬ F ∨ T ∨ F) ∧
+ (T ∨ T ∨ ¬ F) ∧ (¬ F ∨ ¬ T ∨ ¬ F) \\
+
+&= (T) ∧ (T) ∧ (T) ∧ (T) \\
+
+&= T \\
+\end{align*}
+$$
+
+Eso fue fácil de verificar, pero descubrir la solución para una fórmula booleana muy grande podría requerir tiempo exponencial. Encontrar una solución para una fórmula booleana es un problema NP en sí mismo: puede requerir recursos exponenciales para encontrar la solución, pero verificarla se puede hacer en tiempo polinomial.
+
+Pero debemos enfatizar: nuestro uso de fórmulas booleanas no es para resolverlas, solo para verificar las soluciones propuestas para ellas.
+
+### Todos los problemas en P y NP se pueden verificar transformándolos en fórmulas booleanas y mostrando una solución a la fórmula
+En los siguientes ejemplos, la entrada es un problema P o NP y la salida es una fórmula booleana. Si conocemos la solución al problema original, entonces también sabremos la solución a la fórmula booleana.
+
+Nuestra intención es mostrar que conocemos el testigo del problema original, pero en forma booleana.
+
+#### Ejemplo 1: verificar si una lista está ordenada usando una fórmula booleana
+Considere los números binarios de un bit $A$ y $B$. La siguiente tabla de verdad devuelve verdadero cuando $A > B$:
+
+| A | B | A > B |
+| --- | --- | --- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
+
+La columna $A > B$ se puede modelar con la expresión $A ∧ ¬B$, que devuelve verdadero en la única fila donde $A > B$ es uno.
+
+Ahora considere una tabla que expresa $A = B$:
+
+| A | B | A = B |
+| --- | --- | --- |
+| 0 | 0 | 1 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
+
+La columna $A = B$ se puede modelar con la expresión $(A ∧ B) ∨ ¬(A ∨ B)$. $(A ∧ B)$ devuelve verdadero cuando $A = 1$ y $B = 1$ y $¬(A ∨ B)$ devuelve verdadero cuando $A$ y $B$ son ambos cero.
+
+Las expresiones para números de un bit:
+
+$$
+\begin{align*}
+A > B &\rightarrow A ∧ ¬B \\
+A = B &\rightarrow (A ∧ B) ∨ ¬(A ∨ B)
+\end{align*}
+$$
+
+serán útiles en breve.
+
+Ahora, ¿cómo comparamos números binarios de más de un bit?
+
+##### Comparación binaria por el bit más significativo diferente
+Suponga que comienza desde el bit más significativo (MSB) más a la izquierda de ambos números y se mueve hacia el bit menos significativo (LSB) de la derecha. En el primer bit, donde los dos números difieren:
+
+Si $P$ tiene un valor de $1$ en ese bit y $Q$ tiene un valor de $0$, entonces $P ≥ Q$.
+La siguiente animación ilustra el algoritmo que detecta que $P ≥ Q$:
+
+
+
+Si $P = Q$, entonces todos los bits son iguales. $P = Q$ significa que $P ≥ Q$ también es cierto:
+
+
+Si P < Q, entonces detectaremos que en el primer bit donde Q es 1 y P es 0:
+
+
+
+Supongamos, sin pérdida de generalidad, que numeramos los bits en $P$ como $p₄, p₃, p₂, p₁$ y los bits en $Q$ como $q₄, q₃, q₂, q₁$.
+
+Si $P ≥ Q$ entonces una de las siguientes condiciones debe ser verdadera:
+- $p₄ > q₄$
+- $p₄ = q₄$ y $p₃ > q₃$
+- $p₄ = q₄$ y $p₃ = q₃$ y $p₂ > q₂$
+- $p₄ = q₄$ y $p₃ = q₃$ y $p₂ = q₂$ y $(p₁ > q₁ \text{ or } p₁ = q₁)$
+
+Podemos combinar los puntos en una sola ecuación.
+
+$$
+\begin{align*}
+&((p₄ > q₄)) ∨ \\
+&((p₄ = q₄) ∧ (p₃ > q₃)) ∨ \\
+&((p₄ = q₄) ∧ (p₃ = q₃) ∧ (p₂ > q₂)) ∨ \\
+&((p₄ = q₄) ∧ (p₃ = q₃) ∧ (p₂ = q₂) ∧ ((p₁ > q₁) ∨ (p₁ = q₁)))
+\end{align*}
+$$
+
+Recuerde nuestras expresiones booleanas que modelaron la igualdad y comparación de un bit:
+
+$$
+\begin{align*}
+A > B &== A ∧ ¬B\\
+A = B y== (A ∧ B) ∨ ¬(A ∨ B)
+\end{align*}
+$$
+
+Podemos sustituir las expresiones para la fórmula $A > B$ y $A = B$ en la ecuación anterior. Para evitar un muro de matemáticas, mostramos las operaciones en formato de video a continuación:
+
+
+
+La fórmula booleana final que expresa $P ≥ Q$, para 4 bits, es:
+
+$$
+\begin{align*}
+&(p₄ ∧ ¬q₄) ∨ \\
+&(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ (p₃ ∧ ¬q₃)) ∨ \\
+&(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ ((p₃ ∧ q₃) ∨ ¬(p₃ ∨ q₃)) ∧ (p₂ ∧ ¬q₂)) ∨ \\
+&(((p₄ ∧ q₄) ∨ ¬(p₄ ∨ q₄)) ∧ ((p₃ ∧ q₃) ∨ ¬(p₃ ∨ q₃)) ∧ ((p₂ ∧ q₂) ∨ ¬(p₂ ∨ q₂)) ∧ ((p₁ ∧ ¬q₁) ∨ ((p₁ ∧ q₁) ∨ ¬(p₁ ∨ q₁))))
+\end{align*}
+$$
+
+Llamemos a una expresión booleana que compara dos números binarios de la manera descrita anteriormente una "expresión de comparación".
+
+##### Cómo comprobar si una lista está ordenada
+Dada una fórmula booleana para comparar números de un tamaño fijo, podemos aplicar repetidamente la expresión de comparación a cada par de elementos adyacentes de la lista y combinar las expresiones de comparación utilizando la operación AND. La lista está ordenada si y solo si la operación AND de todas las expresiones de comparación es verdadera.
+
+Por lo tanto, vemos que un testigo que demuestra que una lista está ordenada no tiene por qué ser la lista ordenada. También puede ser la entrada a la fórmula booleana que creamos anteriormente que da como resultado que la fórmula devuelva verdadero.
+
+#### Ejemplo 2: Un coloreado de 3 colores como una fórmula booleana
+Veamos nuestro mapa de Australia nuevamente:
+
+
+
+Para modelar la solución como una fórmula booleana, la fórmula debe codificar los siguientes hechos:
+
+- Cada territorio tiene uno de tres colores
+- Cada territorio tiene un color diferente al de su vecino
+
+Por ejemplo, para decir que Australia Occidental es verde, azul o roja, necesitamos crear tres Variables `WESTERN_AUSTRALIA_GREEN`, `WESTERN_AUSTRALIA_BLUE`,`WESTERN_AUSTRALIA_RED`. Para evitar nombres de variable largos, las llamaremos `WA_G`, `WA_B` y `WA_R`. Nuestra fórmula booleana es entonces:
+
+```
+(WA_G ∧ ¬WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ ¬WA_B ∧ WA_R)
+```
+
+En otras palabras:
+
+"(Australia Occidental es verde Y Australia Occidental NO es azul Y Australia Occidental NO es roja)
+
+O
+
+(Australia Occidental NO es verde Y Australia Occidental es azul Y Australia Occidental NO es roja)
+
+O
+
+(Australia Occidental NO es verde Y Australia Occidental NO es azul Y Australia Occidental es roja)"
+
+Coloreando la fórmula booleana para enfatizar:
+
+(WA_G ∧ ¬WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ ¬WA_B ∧ WA_R)
+
+Llamemos a la fórmula anterior *restricción de asignación de color*.
+
+Usamos variables booleanas para codificar el color asignado a un territorio. Dado que una variable booleana solo puede contener dos valores, pero un territorio puede tener uno de tres colores, a cada territorio se le asignan tres variables booleanas, una para cada color. Si a un territorio se le asigna un color en particular, la variable correspondiente se establece en verdadero y las demás se establecen en falso.
+
+La fórmula anterior es verdadera si y solo si al territorio de Australia Occidental se le asigna exactamente un color.
+
+##### Restricción de color vecina
+A continuación, queremos escribir una fórmula que exprese que WA tiene un color diferente al de su vecina. Creamos tres variables para SA (Australia del Sur) como hicimos para WA. Ahora, nuestra fórmula simplemente dice: "para cada color, WA y SA no son ambos de ese color". Esto es equivalente a decir "WA y SA no son del mismo color". Usemos los nombres de variable `SA_G`, `SA_B` y `SA_R` para referirnos a la asignación de color de Australia del Sur (que es vecina de Australia Occidental). Usamos la siguiente fórmula para expresar que tienen diferentes colores:
+
+¬(WA_G ∧ SA_G) ∧ ¬(WA_B ∧ SA_B) ∧ ¬(WA_R ∧ SA_R)
+
+En otras palabras:
+
+**NO** es el caso de que (Australia Occidental sea verde Y Australia del Sur sea verde)
+
+**Y**
+
+**NO** es el caso de que (Australia Occidental sea azul Y Australia del Sur sea azul)
+
+**Y**
+
+**NO** es el caso de que (Australia Occidental sea azul) es rojo Y Australia del Sur es rojo)"
+
+La fórmula anterior se cumplirá si y solo si a Australia Occidental y Australia del Sur no se les asignó el mismo color. Llamemos a la fórmula anterior *restricción de límite*.
+
+Necesitamos aplicar la restricción de asignación de color a cada territorio y la restricción de color diferente a cada par de vecinos, luego aplicar Y a todas las restricciones juntas.
+
+##### Una fórmula para modelar una coloración 3 de Australia
+Ahora mostramos la fórmula booleana final que verifica una coloración 3 válida para Australia. Aquí están los territorios etiquetados:
+
+
+
+Primero, asignamos a cada territorio un nombre de variable:
+
+- `WA` = Australia Occidental
+- `SA` = Australia del Sur
+- `NT` = Territorio del Norte
+- `Q` = Queensland
+- `NSW` = Nueva Gales del Sur
+- `V` = Victoria
+
+###### Restricciones de color: Cada uno de los seis territorios tiene exactamente un color:
+
+
+
+1. (WA_G ∧ ¬WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ WA_B ∧ ¬WA_R) ∨ (¬WA_G ∧ ¬WA_B ∧ WA_R)
+
+2. (SA_G ∧ ¬SA_B ∧ ¬SA_R) ∨ (¬SA_G ∧ SA_B ∧ ¬SA_R) ∨ (¬SA_G ∧ ¬SA_B ∧ SA_R)
+
+3. (NT_G ∧ ¬NT_B ∧ ¬NT_R) ∨ (¬NT_G ∧ NT_B ∧ ¬NT_R) ∨ (¬NT_G ∧ ¬NT_B ∧ NT_R)
+
+4. (Q_G ∧ ¬Q_B ∧ ¬Q_R) ∨ (¬Q_G ∧ Q_B ∧ ¬Q_R) ∨ (¬Q_G ∧ ¬Q_B ∧ Q_R)
+
+5. (NSW_G ∧ ¬NSW_B ∧ ¬NSW_R) ∨ (¬NSW_G ∧ NSW_B ∧ ¬NSW_R) ∨ (¬NSW_G ∧ ¬NSW_B ∧ NSW_R)
+
+6. (V_G ∧ ¬V_B ∧ ¬V_R) ∨ (¬V_G ∧ V_B ∧ ¬V_R) ∨ (¬V_G ∧ ¬V_B ∧ V_R)
+
+
+
+###### Restricciones de límites: cada territorio vecino no comparte un color
+
+A continuación, iteramos a través de los límites y calculamos una restricción de límites para esos vecinos. El siguiente video muestra el algoritmo en acción. Mostramos el conjunto final de fórmulas para las condiciones de límites después del video:
+
+
+
+7. Australia Occidental y Australia del Sur:
+
+¬(WA_G ∧ SA_G) ∧ ¬(WA_B ∧ SA_B) ∧ ¬(WA_R ∧ SA_R)
+
+8. Australia Occidental y Territorio del Norte:
+
+¬(WA_G ∧ NT_G) ∧ ¬(WA_B ∧ NT_B) ∧ ¬(WA_R ∧ NT_R)
+
+9. Territorio del Norte y Australia del Sur:
+
+¬(NT_G ∧ SA_G) ∧ ¬(NT_B ∧ SA_B) ∧ ¬(NT_R ∧ SA_R)
+
+10. Territorio del Norte y Queensland:
+
+¬(NT_G ∧ Q_G) ∧ ¬(NT_B ∧ Q_B) ∧ ¬(NT_R ∧ Q_R)
+
+11. Australia del Sur y Queensland:
+
+¬(SA_G ∧ Q_G) ∧ ¬(SA_B ∧ Q_B) ∧ ¬(SA_R ∧ Q_R)
+
+12. Australia del Sur y Nueva Gales del Sur:
+
+¬(SA_G ∧ NSW_G) ∧ ¬(SA_B ∧ NSW_B) ∧ ¬(SA_R ∧ NSW_R)
+
+13. Australia del Sur y Victoria:
+
+¬(SA_G ∧ V_G) ∧ ¬(SA_B ∧ V_B) ∧ ¬(SA_R ∧ V_R)
+
+14. Queensland y Nueva Gales del Sur:
+
+¬(Q_G ∧ NSW_G) ∧ ¬(Q_B ∧ NSW_B) ∧ ¬(Q_R ∧ NSW_R)
+
+15. Nueva Gales del Sur y Victoria:
+
+¬(NSW_G ∧ V_G) ∧ ¬(NSW_B ∧ V_B) ∧ ¬(NSW_R ∧ V_R)
+
+Creamos una fórmula booleana tomando el AND booleano de las 15 fórmulas mencionadas anteriormente. Tener una asignación a las variables que dé como resultado que el resultado de la expresión booleana sea verdadero es equivalente a tener una coloración 3 válida de Australia.
+
+En otras palabras, si conocemos una coloración 3 válida para Australia, entonces también conocemos una asignación a la fórmula booleana construida anteriormente.
+
+### La fórmula booleana debe ser construible en tiempo polinomial
+Solo necesitamos tomar una cantidad polinomial de pasos para construir esta fórmula booleana para la coloración 3. Específicamente, necesitamos:
+
+- 3 restricciones de color por territorio
+- Como máximo N restricciones de color vecinas por territorio
+
+Es un requisito que los pasos tomados para construir la fórmula booleana se realicen en tiempo polinomial. Si se requiere una cantidad exponencial de pasos, entonces la fórmula booleana será exponencialmente grande y el testigo será exponencialmente grande, y no verificable en tiempo polinomial.
+
+### Resumen del uso de expresiones booleanas para modelar problemas y soluciones propuestas
+Todos los problemas en P y NP se pueden expresar como una fórmula booleana que da como resultado verdadero si conocemos la asignación de variable correspondiente (testigo), que codifica una solución correcta al problema original.
+
+Ahora que tenemos un lenguaje estándar para demostrar eficientemente una solución a un problema, estamos un paso más cerca de un método estándar para demostrar que tenemos una solución a un problema, sin revelar la solución, es decir, Zero Knowledge Proofs.
+
+## Parte 3: P vs NP y ZK Proofs
+### Cómo se relaciona P = NP con las ZK Proofs
+El "conocimiento" en las Zero Knowledge Proofs se refiere al conocimiento del testigo.
+
+Las ZK proofs se ocupan del aspecto de verificación del cálculo. Es decir, dado que ha encontrado una solución de Sudoku o una coloración triple de un mapa, ¿puede darle a alguien evidencia (testigo) que le permita verificar eficientemente que su solución es correcta?
+
+Las ZK proofs buscan demostrar que usted conoce al testigo sin revelarlo.
+
+### Las ZK Proofs solo funcionan con problemas P o NP. No se pueden usar para problemas que no podemos verificar eficientemente.
+Si no tenemos un mecanismo para probar eficientemente que las expresiones regulares son equivalentes, o que un cierto movimiento en ajedrez es óptimo, entonces las ZK Proofs no pueden permitirnos mágicamente producir una prueba tan eficiente.
+
+Para los problemas P y NP, la verificación de la solución se puede hacer eficientemente. ZK permite verificar que la solución es válida mientras oculta los detalles del cálculo. Además, ZK no puede ayudarlo a descubrir una solución para un sudoku o descubrir una coloración triple de un mapa. Sin embargo, puede ayudarlo a probarle a otra parte que tiene una solución, si ya la calculó.
+
+### La conexión entre P vs NP y las Zero Knowledge Proofs
+
+**Todos los problemas con soluciones que se pueden verificar rápidamente se pueden convertir en una fórmula booleana.**
+
+Poder convertir cualquier problema en una fórmula booleana no es un truco para encontrar la respuesta de manera eficiente. Resolver una expresión booleana arbitraria es un problema NP y encontrar una solución puede ser difícil.
+
+El tamaño de la fórmula booleana es importante. Volviendo a nuestro ejemplo de ajedrez, si intenta modelar cada estado con una fórmula booleana, entonces el tamaño de su fórmula será exponencialmente grande. Por lo tanto, los únicos problemas factibles son NP o P, que tienen fórmulas booleanas de tamaño razonable que los modelan.
+
+**En la literatura de ZK, a menudo nos referimos a las fórmulas booleanas como circuitos booleanos.**
+
+Crear una zero knowledge proof para un problema se reduce a traducir el problema a un circuito, como se demuestra al probar una tricoloración para Australia o validar una lista ordenada. Luego, demuestras que tienes una entrada válida al circuito (el testigo), que finalmente se transforma en una prueba de conocimiento cero.
+
+La capacidad de verificar eficientemente una solución a un problema es un prerrequisito para crear una zero knowledge proof de que tienes una solución. Uno debe ser capaz de construir un circuito booleano para modelar la solución de manera eficiente. Sin embargo, para problemas como determinar movimientos óptimos de ajedrez, que pertenecen a PSPACE, este enfoque da como resultado circuitos exponencialmente grandes, lo que los hace poco prácticos.
+
+En conclusión, las pruebas de conocimiento cero son factibles solo para problemas dentro de P y NP, donde es posible una verificación eficiente de la solución. Sin una verificación eficiente, crear una prueba de conocimiento cero para un problema se vuelve inviable.
+
+## Más información
+Consulta el [Libro de ZK de RareSkills](https://www.rareskills.io/zk-book) para obtener más temas sobre zero knowledge proofs.
+
+## Aspectos técnicos
+En este artículo se han simplificado algunos conceptos para que sean lo más comprensibles posible para alguien que los vea por primera vez. La información presentada aquí es suficiente para explicar lo que las ZK Proofs pueden y no pueden hacer. Para aquellos interesados en profundizar en el tema, aquí hay algunas aclaraciones:
+
+- A un tablero de ajedrez de un tamaño fijo $(8 \times 8)$ no se le puede asignar un nivel de dificultad porque la dificultad del problema no se puede expresar como $\mathcal{O}(f(n))$. Técnicamente, decimos que el ajedrez de un tamaño arbitrario es PSPACE. Puede resultar confuso pensar en un tablero de ajedrez de $10 \times 10$, pero uno puede simplemente especificar que los espacios adicionales no tienen ninguna pieza en ellos en la posición inicial.
+
+- El ajedrez tiene una regla menos conocida que establece que si no se ha producido ningún movimiento de captura y ningún peón se ha movido durante los últimos 50 movimientos, entonces un jugador puede declarar tablas. Esto coloca un límite en el espacio de búsqueda que lo coloca en PSPACE. Si se elimina esta regla, entonces esta versión de ajedrez está en EXPSPACE, una categoría de problemas que requiere tiempo exponencial y tamaño de memoria exponencial para calcularse.
+
+- Algunos problemas NP se pueden resolver en *tiempo sub-exponencial*, pero para fines prácticos, su resolución lleva tiempo exponencial. Por ejemplo, $\mathcal{O}(2^{\sqrt{n}})$ es técnicamente sub-exponencial, pero sigue siendo exponencialmente difícil.
+
+- Existen heurísticas muy poderosas para encontrar soluciones a algunos problemas NP. Aunque resolver tres coloraciones lleva un tiempo exponencial, muchas instancias del problema de tamaño razonable se pueden resolver rápidamente. Por ejemplo, [aquí hay problemas de referencia de mapas con 200 territorios y 3 coloraciones válidas](https://www.cs.ubc.ca/~hoos/SATLIB/benchm.html). Los algoritmos inteligentes pueden encontrar la solución sin explorar un espacio de búsqueda exponencialmente grande. Sin embargo, para cualquier heurística diseñada para acelerar la resolución de un problema NP, es posible crear una instancia patológica del problema que esté diseñada para explotar la heurística y hacerla inútil. Sin embargo, la heurística funciona bien para el caso típico de un ejemplo realista del problema.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/pedersen-commitment_es.md b/spanish-es/pedersen-commitment_es.md
new file mode 100644
index 0000000..479f63d
--- /dev/null
+++ b/spanish-es/pedersen-commitment_es.md
@@ -0,0 +1,203 @@
+# ¿Qué son los compromisos de Pedersen y cómo funcionan?
+Los compromisos de Pedersen nos permiten codificar vectores arbitrariamente grandes con un único punto de curva elíptica, mientras que opcionalmente ocultamos cualquier información sobre el vector.
+
+Nos permite hacer afirmaciones sobre un vector sin revelar el vector en sí.
+
+## Motivación
+Cuando hablamos de pruebas de conocimiento cero a prueba de balas, generalmente serán de la forma "Tengo dos vectores cuyo producto interno es $v$". Esto puede parecer básico, pero en realidad puedes usar este mecanismo para probar afirmaciones muy no triviales. Llegaremos a eso más adelante.
+
+Pero para que una prueba de este tipo funcione, los vectores no pueden simplemente existir en la cabeza del probador; de lo contrario, el probador puede cambiarlos a voluntad. Tienen que ser entidades matemáticas en el mundo real. Generalmente, el probador no quiere simplemente pasar los dos vectores al verificador, pero aún necesita "pasar algo" al verificador para representar que ha seleccionado un par de vectores y no puede cambiarlo.
+
+Aquí es donde entran en escena los compromisos de Pedersen.
+
+En un argumento de producto interno, el demostrador proporciona dos *compromisos* con dos vectores, luego proporciona una prueba de que los vectores comprometidos tienen un determinado producto interno.
+
+## Requisitos previos
+Suponemos que el lector ya está familiarizado con la [suma de puntos de curva elíptica](https://www.rareskills.io/post/elliptic-curve-addition) y la multiplicación escalar y lo que significa que un punto esté "en la curva".
+
+En cuanto a la notación, las letras mayúsculas son puntos de curva elíptica, las letras minúsculas son elementos de campo finito.
+
+Decimos que $A$ es un punto de curva elíptica (EC), a es un elemento de [campo finito](rareskills.io/post/finite-fields) y $aA$ es la multiplicación de puntos entre el elemento de campo finito $a$ y el punto EC $A$. La expresión $A + B$ denota la suma de puntos de curva elíptica.
+
+## Compromisos tradicionales
+Cuando diseñamos funciones de revelación de confirmación en contratos inteligentes, normalmente tienen la forma
+
+$$
+\text{commitment} = \mathsf{hash}(\text{value}, \text{salt})
+$$
+
+donde $\text{salt}$ es un valor aleatorio para evitar que un atacante adivine por fuerza bruta $\text{value}$.
+
+Por ejemplo, si estuviéramos confirmando un voto, solo hay una cantidad limitada de opciones y, por lo tanto, la selección del voto se puede adivinar probando todos los votos para ver qué hash coincide.
+
+La terminología académica para la variable *salt* en el caso de los compromisos de Pedersen es el *factor cegador*. Debido a que es aleatorio, el atacante está "ciego" y no puede adivinar el valor confirmado.
+
+Debido a que un adversario no puede adivinar el valor "compromiso", decimos que este esquema de compromiso es *oculto*.
+
+Durante la fase de revelación, el autor revela el valor y la sal, para que la otra parte (o el contrato inteligente) pueda validar que coincide con el compromiso original. No es posible obtener otro par $(\text{value}, \text{salt})$ que pueda dar como resultado el mismo compromiso, por lo que decimos que este esquema es vinculante: el autor no puede cambiar (es decir, está obligado a) su valor comprometido después del hecho.
+
+Un par $(\text{value}, \text{salt})$ que da como resultado el hash se denomina *apertura*. Decir que alguien "conoce una apertura al compromiso" significa que conoce (valor, sal). *Revelar* $(\text{value}, \text{salt})$ significa *abrir* el compromiso.
+
+Al hablar de los compromisos de Pedersen, existe una distinción entre *conocer la apertura* y *abrir* el compromiso. Por lo general, queremos demostrar que *conocemos* la apertura, pero no necesariamente *abrirla*.
+
+## Resumen de terminología
+- Un compromiso **oculto** no permite que un adversario sepa qué valor seleccionó el autor del compromiso. Esto se logra generalmente incluyendo un término aleatorio que el atacante no puede adivinar.
+- Un término **cegador** es el número aleatorio que hace que el compromiso sea imposible de adivinar.
+- Una **apertura** son los valores que se calcularán para el compromiso.
+- Un compromiso **vinculante** no permite que el autor del compromiso calcule un hash con diferentes valores. Es decir, no puede encontrar dos pares (valor, sal) que generen el mismo valor.
+
+## Compromisos de Pedersen
+Los compromisos de Pedersen se comportan de manera muy similar al esquema de confirmación-revelación descrito anteriormente, excepto que utilizan grupos de curvas elípticas en lugar de funciones hash criptográficas.
+
+Bajo el supuesto de logaritmo discreto, dados los puntos de curva elíptica $V$ y $U$, no podemos calcular $x$ donde $V$ = $xU$. Es decir, no conocemos su *relación de logaritmo discreto*, es decir, cuántas veces $V$ debe sumarse a sí mismo para obtener $U$.
+
+Cuando decimos que $u$ es el logaritmo discreto de $U$, todavía nos referimos a $u$ como el logaritmo discreto de $U$ aunque no podamos calcularlo, porque sabemos que existe. Todos los puntos de curva elíptica (criptográficos) tienen un logaritmo discreto, incluso si no se pueden calcular.
+
+En este sentido, la multiplicación de puntos de curva elíptica se comporta como una función hash. Son vinculantes siempre que solo permitamos aperturas dentro del orden de la curva.
+
+Sin embargo, si el rango de logaritmos discretos es pequeño y está limitado por el contexto de la aplicación (como las opciones de votación), entonces el logaritmo discreto podría volverse adivinable.
+
+Podemos hacer un escondite de Pedersen de la siguiente manera:
+
+$$
+\text{commitment} = vG + sB
+$$
+
+donde $v$ es el valor que estamos confirmando y $s$ es la sal (o factor de cegamiento) y $B$ es otro punto de la curva elíptica cuyo logaritmo discreto el confirmador no conoce.
+
+Debemos enfatizar que, aunque los logaritmos discretos son desconocidos, los puntos $G$ y $B$ son públicos y conocidos tanto por el verificador como por el confirmador.
+
+### Por qué el confirmador no debe conocer el logaritmo discreto de $Q$
+Supongamos que el confirmador conoce la relación de logaritmo discreto entre $B$ y $G$. Es decir, conocen $u$ tal que $B = uG$.
+
+En ese caso, pueden abrir el compromiso
+
+$$
+\text{commitment} = vG + sB
+$$
+
+a un $(v', s')$ diferente del valor que originalmente comprometieron.
+
+Así es como el autor del compromiso podría hacer trampa si sabe que $g$ es el logaritmo discreto de $G$ y $b$ es el logaritmo discreto de $B$.
+
+El autor del compromiso elige un nuevo valor $v'$ y calcula
+
+$$
+s' = \frac{\text{commitment}- v'g}{b}
+$$
+
+Luego, el probador presenta $(v', s')$ como la apertura falsificada.
+
+Esto funciona porque
+$$
+\begin{align*}
+\text{commitment} &= v'G + \frac{\text{commitment}- v'g}{b} B \\
+\text{commitment} &= v'G + (\text{commitment}- v'gG) \\
+\text{commitment} &= \text{commitment} \\
+\end{align*}
+$$
+
+**El autor de la confirmación no debe conocer la relación logarítmica discreta entre los puntos de la curva elíptica que está utilizando.**
+
+Una forma de lograr esto es que un verificador proporcione los puntos de la curva elíptica al autor de la confirmación. Sin embargo, una forma más sencilla es elegir los puntos de la curva elíptica de forma aleatoria y transparente, como por ejemplo seleccionando puntos de la curva elíptica de forma pseudoaleatoria. Dado un punto de la curva elíptica aleatorio, no conocemos su logaritmo discreto.
+
+Por ejemplo, podríamos empezar con el punto generador, hacer un hash de los valores $x$ e $y$, y luego usarlo para generar una búsqueda pseudoaleatoria pero determinista para el siguiente punto.
+
+## ¿Por qué son útiles los compromisos de Pedersen?
+Parece que los compromisos de Pedersen son solo una revelación de compromiso normal con una función hash diferente, entonces, ¿cuál es el punto?
+
+Este esquema tiene un par de ventajas.
+
+### Los compromisos de Pedersen son homomórficos aditivamente
+Dado un punto $G$, podemos sumar dos compromisos $a_1G + a_2G$ = $(a_1 + a_2)G$.
+
+Si incluimos términos de cegamiento aleatorios, aún podemos hacer una apertura válida sumando los términos de cegamiento y proporcionándoselos al verificador. Sea $C$ compromisos. Ahora, pensemos en lo que sucede cuando sumamos $C_1 + C_2$:
+
+$$
+\begin{aligned}
+C_1 &= a_1G + s_1B \\
+C_2 &= a_2G + s_2B \\
+C_3 &= C_1 + C_2 \\
+\pi &= s_1 + s_2 \\
+\text{el confirmador revela...} \\
+&(a_1, a_2, \pi) \\
+\text{y el verificador comprueba...} \\
+C_3 &\stackrel{?}{=} a_1G + a_2G + \pi B
+\end{aligned}
+$$
+
+Alternativamente, el verificador puede comprobar que
+
+$$C_3 = (a_1 + a_2)G + \pi B$$
+
+Los hashes regulares (como SHA-256) no se pueden sumar de esta manera.
+
+Dados dos compromisos de Pedersen que utilizan los mismos puntos de curva elíptica para comprometerse, podemos sumar los compromisos y aún así tener una apertura válida para ellos.
+
+Los compromisos de Pedersen permiten que un probador haga afirmaciones sobre las sumas de los valores comprometidos.
+
+### Podemos codificar tantos puntos como queramos en un solo punto
+Nuestro ejemplo de uso de $G$ y $B$ también puede considerarse como un compromiso de vector 2D sin un término cegador. Pero podemos agregar tantos puntos de curva elíptica como queramos $[G₁, G₂, …, Gₙ]$ y comprometer tantos escalares como queramos. (Aquí, $G_1$, $G_2$, etc. significan diferentes puntos en el mismo grupo, no generadores de diferentes grupos).
+
+## Compromisos de vector de Pedersen
+Podemos tomar el esquema anterior como un paso más y comprometer un conjunto de valores en lugar de un valor y un término cegador.
+
+## Esquema de compromiso de vector
+Supongamos que tenemos un conjunto de puntos de curva elíptica aleatorios $(G₁,…,Gₙ)$ (del que no conocemos el logaritmo discreto), y hacemos lo siguiente:
+
+$$C_1 = \underbrace{v_1G_1 + v_2G_2 + … + v_nG_n}_\text{vector comprometido} + \underbrace{sB}_\text{término ciego}$$
+
+Esto nos permite comprometer $n$ valores a $C$ y ocultarlo con $s$.
+
+Como el comprometidor no conoce el logaritmo discreto de ninguno de $G_i$, no conoce el logaritmo discreto de $C$. Por lo tanto, este esquema es vinculante: solo puede revelar $(v₁,…,vₙ)$ para producir $C$ más tarde, no puede producir otro vector.
+
+### Los compromisos de vector se pueden combinar
+Podemos sumar dos compromisos de vector de Pedersen para obtener un compromiso con dos vectores. Esto solo permitirá que el comprometidor abra los vectores originales. El detalle de implementación importante es que tenemos que usar un conjunto diferente de puntos de curva elíptica para comprometerse.
+
+$$
+\begin{align*}
+C_1 &= v_1 G_1 + v_2 G_2 + \ldots + v_n G_n + r B \\
+C_2 &= w_1 H_1 + w_2 H_2 + \ldots + w_n H_n + s B \\
+C_3 &= C_1 + C_2
+\end{align*}
+$$
+
+Al sumar $C_1$ y $C_2$, estamos comprometiendo funcionalmente un vector más grande de tamaño $2n$.
+
+Aquí, $rB$ y $sB$ son los términos cegadores. Incluso si el autor confirma el vector cero, la confirmación seguirá pareciendo un punto aleatorio.
+
+El autor revelará más tarde los vectores originales $(v₁…vₙ)$ y $(w₁…wₙ)$ y el término cegador $r + s$. Esto es vinculante: no pueden revelar otro par de vectores y términos cegadores.
+
+El hecho de que estemos usando $(G₁,…,Gₙ)$ para un vector y $(H₁,…,Hₙ)$ no debería implicar que exista una relación especial entre los puntos $G$ y una relación especial entre los puntos $H$. Todos los puntos deben seleccionarse de forma pseudoaleatoria. Esto es simplemente una conveniencia de notación para decir "este vector de puntos de curva elíptica va con este vector de elementos de campo, y este otro vector de puntos EC va con este otro vector de elementos de campo".
+
+No existe un límite superior práctico para la cantidad de vectores que podemos confirmar.
+
+**Ejercicio para el lector:** Si usamos el mismo $G₁…Gₙ$ para ambos vectores antes de sumarlos, ¿cómo podría un autor abrir dos vectores diferentes para $C_3$? Dé un ejemplo. ¿Cómo se evita esto utilizando un conjunto diferente de puntos $H₁…Hₙ$?
+
+**Ejercicio para el lector:** ¿Qué sucede si el autor intenta intercambiar los mismos elementos dentro del vector?
+
+Por ejemplo, hacen el envío:
+
+$$C_1 = v_1G_1 + v_2G_2 + \ldots + v_nG_n + rB$$
+
+Pero abren con los dos primeros elementos intercambiados:
+
+$$[v_2, v_1, v_3, ..., v_n]$$
+
+Es decir, intercambian los dos primeros elementos dejando todo lo demás sin cambios. Supongamos que el vector $G₁…Gₙ$ no está permutado.
+
+## Generar puntos aleatorios de forma transparente
+¿Cómo podemos generar estos puntos aleatorios de curva elíptica? Una solución obvia es utilizar una configuración de confianza, pero no es necesaria. El autor de la confirmación puede configurar los puntos de forma que no pueda conocer su logaritmo discreto seleccionando aleatoriamente los puntos de forma transparente.
+
+Puede elegir el punto generador, mezclarlo con un número aleatorio elegido públicamente y hacer un hash de ese resultado (y tomarlo módulo del módulo de campo) para obtener otro valor. Si eso da como resultado un valor x que se encuentra en la curva elíptica, utilícelo como el siguiente generador y haga un hash del par $(x, y)$ nuevamente. De lo contrario, si el valor x no se encuentra en la curva, incremente $x$ hasta que lo haga. Debido a que el autor de la confirmación no está generando los puntos, no conoce su logaritmo discreto. Los detalles de implementación de este algoritmo se dejan como ejercicio para el lector.
+
+En ningún momento se debe generar un punto eligiendo un escalar y luego multiplicándolo por el generador, ya que eso daría como resultado que se conozca el logaritmo discreto. Debe seleccionar los valores $x$ del punto de la curva de forma pseudoaleatoria mediante una función hash y determinar si está en la curva.
+
+Está bien comenzar con el generador (que tiene un logaritmo discreto conocido de 1) y generar los otros puntos.
+
+**Ejercicio para el lector:** Supongamos que confirmamos un vector 2D en los puntos $G_1$ y $G_2$. Se conoce el logaritmo discreto de $G_1$, pero no se conoce el logaritmo discreto de $G_2$. Ignoraremos el término ciego por ahora. ¿Puede el confirmador abrir dos vectores diferentes? ¿Por qué sí o por qué no?
+
+Obtenga más información con RareSkills
+Consulte nuestro campamento de entrenamiento ZK si desea [aprender ZK Proofs](https://www.rareskills.io/zk-bootcamp).
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
diff --git a/spanish-es/pedersen-polynomial-commitment_es.md b/spanish-es/pedersen-polynomial-commitment_es.md
new file mode 100644
index 0000000..4d047eb
--- /dev/null
+++ b/spanish-es/pedersen-polynomial-commitment_es.md
@@ -0,0 +1,155 @@
+# Compromisos polinomiales a través de los compromisos de Pedersen
+
+Un compromiso polinomial es un mecanismo por el cual un probador puede convencer a un verificador de que un polinomio $p$ tiene una evaluación $y = p(x)$ en el punto $x$ sin revelar nada acerca de $p$. La secuencia es la siguiente:
+
+1. El probador envía al verificador un *compromiso* $C$ con el polinomio, "bloqueando" su polinomio.
+2. El verificador responde con un valor $u$ en el que desea que se evalúe el polinomio.
+3. El probador responde con $y$ y $\pi$, donde $y$ es la evaluación de $f(u)$ y $\pi$ es la prueba de que la evaluación fue correcta.
+4. El verificador verifica $C$, $u$, $y$, $\pi$ y acepta o rechaza que la evaluación del polinomio fue válida.
+
+Este esquema de compromiso no requiere una configuración confiable. Sin embargo, la sobrecarga de comunicación es $O(n)$ ya que el probador debe enviar un compromiso para cada coeficiente en su polinomio.
+
+## Los pasos para comprometerse con el polinomio
+### El probador compromete cada coeficiente del polinomio
+El probador puede comprometerse con el polinomio creando un [Compromiso de Pedersen](https://www.rareskills.io/post/pedersen-commitment) de cada coeficiente. Para un Compromiso de Pedersen, el probador y el verificador deben acordar dos puntos de curva elíptica con logaritmos discretos desconocidos. Usaremos $G$ y $B$.
+
+Por ejemplo, si tenemos polinomio
+
+$$f(x) = f_0+f_1x+f_2x^2$$
+
+Donde $f_0$ es el término constante, $f_1$ es el coeficiente lineal y $f_2$ es el coeficiente cuadrático.
+
+Podemos crear un compromiso de Pedersen para cada coeficiente. Necesitaremos tres términos de cegamiento $\gamma_0$, $\gamma_1$, $\gamma_2$. Por conveniencia, cualquier escalar usado para cegar usará una letra griega minúscula. Siempre usamos el punto de curva elíptica $B$ para el término de cegamiento. Nuestros compromisos se producen de la siguiente manera:
+
+$$
+\begin{align*}
+C_0=f_0G+\gamma_0B \\
+C_1=f_1G+\gamma_1B \\
+C_2=f_2G+\gamma_2B \\
+\end{align*}
+$$
+
+El probador envía la tupla $(C_0, C_1, C_2)$ al verificador. Estos son esencialmente compromisos de Pedersen para cada uno de los coeficientes del polinomio $f(x)$.
+
+### El verificador elige $u$
+El verificador elige su valor para $u$ y lo envía al probador.
+
+### El probador evalúa el polinomio y calcula la prueba
+El probador calcula el polinomio original como:
+
+$$
+y = f_0 + f_1u + f_2u^2
+$$
+
+### El probador evalúa los términos ciegos
+La prueba de que la evaluación se realizó correctamente se da mediante el siguiente polinomio, que utiliza los términos ciegos multiplicados por la potencia asociada de $u$. La razón de esto se explicará más adelante.
+
+$$
+\pi = \gamma_0 + \gamma_1u+\gamma_2u^2
+$$
+
+El probador envía $(y, \pi)$ al verificador. Tenga en cuenta que el probador solo envía elementos de campo (escalares), no puntos de curva elíptica.
+
+**La prueba es simplemente la suma de los términos cegadores para cada coeficiente multiplicado por las potencias de $u$ para ese coeficiente.**
+
+## Paso de verificación
+El verificador realiza la siguiente comprobación:
+
+$$
+C_0+C_1u+C_2u^2\stackrel{?}{=}yG+\pi B
+$$
+
+Si el verificador fue honesto, $y$ será la suma de los coeficientes polinómicos multiplicados por potencias sucesivas de $u$, y $\pi$ será la suma de los términos cegadores multiplicados por las potencias de $u$.
+
+## Por qué funciona el paso de verificación
+Si expandimos los puntos de la curva elíptica a sus valores subyacentes, vemos que la ecuación está balanceada:
+
+$$
+\begin{align*}
+C_0 + C_1u + C_2u^2 &= yG + \pi B \\
+(f_0G + \gamma_0B) + (f_1G + \gamma_1B)u + (f_2G + \gamma_2B)u^2 &= (f_0 + f_1u + f_2u^2)G + (\gamma_0 + \gamma_1u + \gamma_2u^2)B \\
+f_0G + \gamma_0B + f_1Gu + \gamma_1Bu + f_2Gu^2 + \gamma_2Bu^2 &= (f_0 + f_1u + f_2u^2)G + (\gamma_0 + \gamma_1u + \gamma_2u^2)B \\
+f_0G + f_1Gu + f_2Gu^2 + \gamma_0B + \gamma_1Bu + \gamma_2Bu^2 &= (f_0 + f_1u + f_2u^2)G + (\gamma_0 + \gamma_1u + \gamma_2u^2)B \\
+(f_0 + f_1u + f_2u^2)G + (\gamma_0 + \gamma_1u + \gamma_2u^2)B &= (f_0 + f_1u + f_2u^2)G + (\gamma_0 + \gamma_1u + \gamma_2u^2)B \\
+\end{align*}
+$$
+
+En cierto sentido, el demostrador está evaluando el polinomio usando los coeficientes del polinomio y su elección de $u$. Esto producirá la evaluación del polinomio original más los términos ciegos del polinomio.
+
+La prueba de una evaluación correcta es que el demostrador puede separar los términos ciegos de la evaluación del polinomio, aunque el demostrador no conozca los logaritmos discretos de $yG$ y $\pi B$.
+
+El siguiente código Python ilustra el algoritmo:
+
+``` python
+import random
+from functools import reduce
+from py_ecc.bn128 import G1, add, eq, field_modulus, multiply
+# WARNING: Points are generated in this manner for convenience. In practice, the point's (g, b) value must be selected randomly and the discrete logs should never be known to anyone.
+g, b = random.randint(1, field_modulus - 1), random.randint(1, field_modulus - 1)
+G, B = multiply(G1, g), multiply(G1, b)
+
+def commit(secret, salt):
+ return add(multiply(G, secret), multiply(B, salt))
+
+# Let's say polynomial be f(x) = x^2 + 2x + 3
+salts = [random.randint(1, 10**9+7) for _ in range(3)]
+C0, C1, C2 = commit(3, salts[0]), commit(2, salts[1]), commit(1, salts[2])
+commitments = [C0, C1, C2]
+u = random.randint(1, 10**9+7) # verifier receives the commitments and responds with u
+y, pi = u**2 + 2*u + 3, salts[2]*u**2 + salts[1]*u + salts[0] # prover computes the value of y and pi and sends it to verifier
+
+def verify(commitments, y, pi):
+ u_powers = [u**i for i in range(len(commitments))]
+ combined_commitment = reduce(add, [multiply(commitments[i], u_powers[i]) for i in range(len(commitments))])
+ commitment_to_y_pi = commit(y, pi)
+ return eq(combined_commitment, commitment_to_y_pi)
+
+is_valid = verify(commitments, y, pi)
+print("Verification result:", is_valid)
+```
+
+## Por qué el probador no puede hacer trampa
+Hacer trampa por parte del probador significa que no evalúa honestamente $y = p(u)$ pero aún así intenta pasar el paso de evaluación final.
+
+Sin pérdida de generalidad, digamos que el probador envía los compromisos correctos para los coeficientes $C_0, C_1, C_2$.
+
+Decimos sin pérdida de generalidad porque hay un desajuste entre los coeficientes enviados en los compromisos y los coeficientes utilizados para evaluar el polinomio.
+
+Para ello, el probador envía $y'$ donde $y' \neq f_0 + f_1u + f_2u^2$.
+
+Usando la ecuación final de la sección anterior, vemos que el probador debe satisfacer:
+
+$$
+(f_0 + f_1u + f_2u^2)G+(\gamma_0 + \gamma_1u+\gamma_2u^2)B=y'G+(\gamma_0 + \gamma_1u+\gamma_2u^2)B
+$$
+
+Los términos $G$ de la ecuación están claramente desequilibrados. La otra "palanca" que puede utilizar el probador es ajustar el $\pi$ que envía.
+
+$$
+(f_0 + f_1u + f_2u^2)G+(\gamma_0 + \gamma_1u+\gamma_2u^2)B=y'G + \boxed{\pi'}B
+$$
+
+Dado que $y' \neq f_0 + f_1u + f_2u^2$, el probador malintencionado debe reequilibrar la ecuación eligiendo un término $\pi'$ que explique la falta de coincidencia en los términos $G$. El probador puede intentar resolver $\pi'$ con
+
+$$
+\pi'B = (f_0 + f_1u + f_2u^2)G+(\gamma_0 + \gamma_1u+\gamma_2u^2)B - y'G
+$$
+
+Pero para resolver esta ecuación, el probador malintencionado debe conocer los logaritmos discretos de $G$ y $B$.
+
+Por ejemplo, si sabemos que el logaritmo discreto de $B$ es $b$ y el logaritmo discreto de $G$ es $g$, entonces podemos calcular $\pi'$ como
+
+$$
+\begin{align*}
+\pi'b = (f_0 + f_1u + f_2u^2)g+(\gamma_0 + \gamma_1u+\gamma_2u^2)b - y'g \\
+\\
+\pi' = \frac{(f_0 + f_1u + f_2u^2)g+(\gamma_0 + \gamma_1u+\gamma_2u^2)b - y'g}{b}
+\end{align*}
+$$
+
+Pero, nuevamente, esto no es posible porque calcular el logaritmo discreto de $B$ y $G$ no es factible.
+
+## Lo que aprende el verificador
+El verificador aprende que los compromisos $C_0, C_1, C_2$ representan compromisos válidos con un polinomio que tiene como máximo grado 2, y que $y$ es el valor del polinomio evaluado en $u$.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
\ No newline at end of file
diff --git a/spanish-es/python-lagrange-interpolation_es.md b/spanish-es/python-lagrange-interpolation_es.md
new file mode 100644
index 0000000..bf5b5e9
--- /dev/null
+++ b/spanish-es/python-lagrange-interpolation_es.md
@@ -0,0 +1,69 @@
+## Interpolación de Lagrange con Python
+
+La interpolación de Lagrange es una técnica para calcular un polinomio que pasa por un conjunto de $n$ puntos.
+
+## Interpolación de un vector como polinomio
+## Ejemplos
+
+### Una línea recta que pasa por dos puntos
+Consideremos que si tenemos dos puntos, se pueden interpolar con una línea. Por ejemplo, dados $(1, 1)$ y $(2, 2)$, podemos dibujar una línea que intersecta ambos puntos, sería un polinomio de grado 1 $y = x$.
+
+### Un solo punto
+Ahora consideremos que si tenemos un punto, podemos dibujar una línea a través de ese punto con un polinomio de grado 0. Por ejemplo, si el punto es $(3, 5)$ podemos dibujar una línea a través de él $y = 5$ (que es un polinomio de grado 0).
+
+### Tres puntos y una parábola
+El patrón de que podemos "dibujar un polinomio a través de" $n$ puntos con un polinomio de grado $n - 1$ (como máximo) se cumple para cualquier número de puntos. Por ejemplo, los puntos $(0, 0), (1, 1), (2, 4)$ se pueden interpolar con $y = x^2$. Si esos puntos fueran una línea recta, por ejemplo $(0, 0), (1, 1), (2, 2)$, entonces podríamos dibujar una línea a través de $(1, 1)$ y $(2, 2)$ con un polinomio de grado 1 $y = x$, pero en general, tres puntos no serán colineales, por lo que necesitaremos un polinomio de grado 2 para cruzar todos los puntos.
+
+## Código Python para la interpolación de Lagrange
+Para nuestros propósitos no es importante entender cómo calcular este polinomio, ya que hay bibliotecas matemáticas que lo harán por nosotros. El algoritmo más común es la *interpolación de Lagrange* y mostramos cómo hacerlo en Python.
+
+#### Ejemplo de coma flotante
+Podemos calcular un polinomio $p(x)$ que cruce los puntos $(1,4), (2,8), (3,2), (4,1)$ usando la interpolación de Lagrange.
+
+```python
+from scipy.interpolate import lagrange
+x_values = [1, 2, 3, 4]
+y_values = [4, 8, 2, 1]
+
+print(lagrange(x_values, y_values))
+# 3 2
+# 2.5 x - 20 x + 46.5 x - 25
+```
+
+#### Ejemplo de campo finito
+Usemos el mismo polinomio que antes, pero esta vez usaremos un campo finito $\mathbb{F}_{17}$ en lugar de números de punto flotante.
+
+```python
+import galois
+import numpy as np
+GF17 = galois.GF(17)
+
+xs = GF17(np.array([1,2,3,4]))
+ys = GF17(np.array([4,8,2,1]))
+
+p = galois.lagrange_poly(xs, ys)
+
+assert p(1) == GF17(4)
+assert p(2) == GF17(8)
+assert p(3) == GF17(2)
+assert p(4) == GF17(1)
+```
+
+### Unicidad del polinomio de interpolación
+Volviendo a nuestro ejemplo de los puntos $(1, 1), (2, 2)$, el polinomio de menor grado que los interpola, $y = x$. En general,
+
+**Para un conjunto de $n$ puntos, existe un único polinomio de grado más bajo de grado $n - 1$ como máximo que los interpola.**
+
+El polinomio de grado más bajo que interpola los polinomios a veces se denomina *polinomio de Lagrange*.
+
+La consecuencia de esto es que
+
+**Si usamos los puntos $(1,2,...,n)$ como los valores $x$ para convertir un vector de longitud $n$ en un polinomio mediante la interpolación de Lagrange, entonces el polinomio resultante es único.**
+
+En otras palabras, dada una base consistente de valores x sobre los cuales interpolar un vector, existe un único polinomio que interpola un vector dado. Dicho de otra manera, cada vector de longitud $n$ tiene una representación polinómica única.
+
+De manera informal, cada vector de grado $n$ tiene un polinomio de grado $n - 1$ único que lo "representa". El grado podría ser menor si, por ejemplo, los puntos son colineales, pero el vector será único.
+
+La parte del "grado más bajo" es importante. Dados dos puntos, hay una cantidad extremadamente grande de polinomios que cruzan esos dos puntos, pero el polinomio de grado más bajo es único.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
\ No newline at end of file
diff --git a/spanish-es/quadratic-arithmetic-program_es.md b/spanish-es/quadratic-arithmetic-program_es.md
new file mode 100644
index 0000000..4cc3d1f
--- /dev/null
+++ b/spanish-es/quadratic-arithmetic-program_es.md
@@ -0,0 +1,756 @@
+# Programas aritméticos cuadráticos
+
+Un programa aritmético cuadrático es un [circuito aritmético](https://www.rareskills.io/post/arithmetic-circuit), específicamente un [sistema de restricciones de Rango 1](https://www.rareskills.io/post/rank-1-constraint-system) (R1CS) representado como un conjunto de polinomios. Se deriva utilizando la interpolación de Lagrange en un sistema de restricciones de rango 1. A diferencia de un R1CS, un programa aritmético cuadrático (QAP) se puede probar para comprobar su igualdad en tiempo $\mathcal{O}(1)$ mediante el lema de Schwartz-Zippel.
+
+## Ideas clave
+En el capítulo sobre el lema de Schwartz-Zippel, vimos que podemos comprobar si dos vectores son iguales en tiempo $\mathcal{O}(1)$ convirtiéndolos en polinomios y luego ejecutando la prueba del lema de Schwartz-Zippel sobre los polinomios. (Para aclarar, la *prueba* es en tiempo $\mathcal{O}(1)$, convertir los vectores en polinomios genera una sobrecarga).
+
+Debido a que un sistema de restricciones de Rango 1 está compuesto completamente de operaciones vectoriales, nuestro objetivo es probar si
+
+$$\mathbf{L}\mathbf{a}\circ\mathbf{R}\mathbf{a}\stackrel{?}{=}\mathbf{O}\mathbf{a}$$
+
+se cumple en tiempo $\mathcal{O}(1)$ en lugar de tiempo $\mathcal{O}(n)$ (donde $n$ es el número de filas en $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$).
+
+Pero antes de hacerlo, debemos comprender algunas propiedades clave de la relación entre los vectores y los polinomios que los representan.
+
+Para todas las matemáticas aquí, asumimos que estamos trabajando en un [campo finito](https://www.rareskills.io/post/finite-fields), pero omitimos la notación $\mod p$ para ser más breves.
+
+## Homomorfismos entre la suma de vectores y la suma de polinomios
+### La suma de vectores es homomórfica a la suma de polinomios
+
+Si tomamos dos vectores, los interpolamos con polinomios y luego sumamos los polinomios, obtenemos el mismo polinomio que si sumamos los vectores y luego interpolamos el vector suma.
+
+Expresado de manera más matemática, sea $\mathcal{L}(\mathbf{v})$ el polinomio resultante de la interpolación de Lagrange sobre el vector $\mathbf{v}$ utilizando $(1, 2, ..., n)$ como los valores de $x$, donde $n$ es la longitud de $\mathbf{v}$. Lo siguiente es cierto:
+
+$$\mathcal{L}(\mathbf{v} + \mathbf{w}) = \mathcal{L}(\mathbf{v}) + \mathcal{L}(\mathbf{w})$$
+
+En otras palabras, los polinomios resultantes de interpolar los vectores $\mathbf{v}$ y $\mathbf{w}$ son los mismos que los polinomios resultantes de interpolar los vectores $\mathbf{v} + \mathbf{w}$.
+
+#### Ejemplo resuelto
+Sea $f_1(x) = x^2$ y $f_2(x) = x^3$ $f_1$ interpola $(1, 1), (2, 4), (3, 9)$ o el vector $[1,4,9]$ y $f_2$ interpola $[1,8,27]$.
+
+La suma de los vectores es $[2,12,36]$ y está claro que $x^3 + x^2$ interpola eso. Sea $f_3(x) = f_1(x) + f_2(x) = x^3 + x^2$.
+
+$$
+\begin{align*}
+f_3(1) &= 1 + 1 = 2\\
+f_3(2) &= 8 + 4 = 12\\
+f_3(3) &= 27 + 9 = 36
+\end{align*}
+$$
+
+#### Probar las matemáticas en Python
+
+Hacer pruebas unitarias de una identidad matemática propuesta no la convierte en verdadera, pero sí ilustra lo que está sucediendo. Se anima al lector a probar algunos vectores diferentes para ver que la identidad se cumple.
+
+```python
+import galois
+import numpy as np
+
+p = 17
+GF = galois.GF(p)
+
+xs = GF(np.array([1,2,3]))
+
+# two arbitrary vectors
+v1 = GF(np.array([4,8,2]))
+v2 = GF(np.array([1,6,12]))
+
+def L(v):
+ return galois.lagrange_poly(xs, v)
+
+assert L(v1 + v2) == L(v1) + L(v2)
+```
+
+### Multiplicación escalar
+Sea $\lambda$ un escalar (específicamente, un elemento de campo en un campo finito). Entonces
+
+$$\mathcal{L}(\lambda \mathbf{v}) = \lambda \mathcal{L}(\mathbf{v})$$
+
+#### Ejemplo resuelto
+Supongamos que nuestros 3 puntos son $[3, 6, 11]$. El polinomio que interpola esto es $f(x) = x^2 + 2$. Si multiplicamos el vector por 3 obtenemos $[9, 18, 33]$. El polinomio que interpola esto es
+
+```python
+from scipy.interpolate import lagrange
+
+x_values = [1, 2, 3]
+y_values = [9, 18, 33]
+
+print(lagrange(x_values, y_values))
+
+# 2
+# 3 x + 6
+```
+
+$3x^2 + 6$, que es igual a $3 \cdot (x^2 + 2)$.
+
+#### Ejemplo resuelto en código
+```python
+import galois
+import numpy as np
+
+p = 17
+GF = galois.GF(p)
+
+xs = GF(np.array([1,2,3]))
+
+# vector arbitrario
+v = GF(np.array([4,8,2]))
+
+# constante arbitraria
+lambda_ = GF(15)
+
+def L(v):
+return galois.lagrange_poly(xs, v)
+
+assert L(lambda_ * v) == lambda_ * L(v)
+```
+
+### La multiplicación escalar es en realidad una suma de vectores
+Cuando decimos "multiplicar un vector por 3", en realidad estamos diciendo "sumar el vector a sí mismo tres veces". Como solo trabajamos en un campo finito, no nos preocupamos por la interpretación de escalares como "0,5".
+
+Podemos pensar en los vectores bajo una suma elemento a elemento (en un campo finito) y en los polinomios bajo una suma (también en un campo finito) como [grupos](https://www.rareskills.io/post/group-theory-and-coding).
+
+La lección más importante de este capítulo es que
+
+**El grupo de vectores bajo adición en un cuerpo finito es homomórfico al grupo de polinomios bajo adición en un cuerpo finito.**
+
+Esto es fundamental porque **la prueba de igualdad de vectores requiere $\mathcal{O}(n)$ tiempo, pero la prueba de igualdad de polinomios requiere $\mathcal{O}(1)$ tiempo.**
+
+Por lo tanto, mientras que la prueba de igualdad de R1CS requiere $\mathcal{O}(n)$ tiempo, podemos aprovechar este homomorfismo para probar la igualdad de R1CS en $\mathcal{O}(1)$ tiempo.
+
+Esto es lo que es un *Programa Aritmético Cuadrático*.
+
+## Un sistema de restricciones de Rango 1 en polinomios
+
+Considere que la multiplicación de matrices entre una matriz rectangular y un vector se puede escribir en términos de adición de vectores y multiplicación escalar.
+
+Por ejemplo, si tenemos una matriz $A$ de $3 \times 4$ y un vector $v$ de 4 dimensiones, entonces podemos escribir la multiplicación de matrices como
+
+$$
+\mathbf{A} \cdot \mathbf{v} = \begin{bmatrix}
+a_{11} & a_{12} & a_{13} & a_{14}\\
+a_{21} & a_{22} & a_{23} & a_{24}\\
+a_{31} & a_{32} & a_{33} & a_{34}
+\end{bmatrix}
+\begin{bmatrix}
+v_1\\
+v_2\\
+v_3\\
+v_4
+\end{bmatrix}
+$$
+
+Normalmente pensamos en el vector $v$ "volteándolo" y haciendo un producto interno (producto escalar generalizado) con cada una de las filas, es decir
+
+$$
+\mathbf{A}\cdot \mathbf{v} =
+\begin{bmatrix}
+a_{11}\cdot v_1 + a_{12}\cdot v_2 + a_{13}\cdot v_3 + a_{14}\cdot v_4\\
+a_{21}\cdot v_1 + a_{22}\cdot v_2 + a_{23}\cdot v_3 + a_{24}\cdot v_4\\
+a_{31}\cdot v_1 + a_{32}\cdot v_2 + a_{33}\cdot v_3 + a_{34}\cdot v_4
+\end{bmatrix}
+$$
+
+Sin embargo, podríamos pensar en dividir la matriz $A$ en un conjunto de vectores de la siguiente manera:
+
+$$
+\mathbf{A} = \begin{bmatrix}
+a_{11} \\
+a_{21} \\
+a_{31}
+\end{bmatrix}
+,
+\begin{bmatrix}
+a_{12} \\
+a_{22} \\
+a_{32}
+\end{bmatrix}
+,
+\begin{bmatrix}
+a_{13} \\
+a_{23} \\
+a_{33}
+\end{bmatrix}
+,
+\begin{bmatrix}
+a_{14} \\
+a_{24} \\
+a_{34}
+\end{bmatrix}
+$$
+
+y multiplicando cada vector por un escalar del vector $\mathbf{v}$:
+
+$$
+\mathbf{A}\cdot \mathbf{v} = \begin{bmatrix}
+a_{11} \\
+a_{21} \\
+a_{31}
+\end{bmatrix}\cdot v_1
++
+\begin{bmatrix}
+a_{12} \\
+a_{22} \\
+a_{32}
+\end{bmatrix}\cdot v_2
++
+\begin{bmatrix}
+a_{13} \\
+a_{23} \\
+a_{33}
+\end{bmatrix}\cdot v_3
++
+\begin{bmatrix}
+a_{14} \\
+a_{24} \\
+a_{34}
+\end{bmatrix}\cdot v_4
+$$
+
+Hemos expresado la multiplicación de matrices entre $\mathbf{A}$ y $\mathbf{v}$ puramente en términos de suma vectorial y multiplicación escalar.
+
+Debido a que establecimos anteriormente que el grupo de vectores bajo adición en un campo finito es homomórfico al grupo de polinomios bajo adición en un campo finito, podemos expresar el cálculo anterior en términos de polinomios que representan los vectores.
+
+## Probando sucintamente que $\mathbf{A}\mathbf{v}_1 = \mathbf{B}\mathbf{v}_2$
+
+Supongamos que tenemos la matriz $\mathbf{A}$ y $\mathbf{B}$ tales que
+
+$$
+\begin{align*}
+\mathbf{A} = \begin{bmatrix}
+6 & 3\\
+4 & 7\\
+\end{bmatrix}\\
+\mathbf{B} = \begin{bmatrix}
+3 & 9 \\
+12 & 6\\
+\end{bmatrix}
+\end{align*}
+$$
+
+y los vectores $\mathbf{v}_1$ y $\mathbf{v}_2$
+
+$$
+\begin{align*}
+\mathbf{v}_1 = \begin{bmatrix}
+2 \\
+4 \\
+\end{bmatrix}\\
+\mathbf{v}_2 = \begin{bmatrix}
+2 \\
+2 \\
+\end{bmatrix}
+\end{align*}
+$$
+
+Queremos comprobar si
+
+$$
+\mathbf{A}\mathbf{v}_1 = \mathbf{B}\mathbf{v}_2
+$$
+
+es verdadero.
+
+Obviamente podemos realizar la aritmética matricial, pero la comprobación final requerirá $n$ comparaciones, donde $n$ es el número de filas en $\mathbf{A}$ y $\mathbf{B}$. Queremos hacerlo en $\mathcal{O}(1)$ tiempo.
+
+Primero, convertimos la multiplicación de matrices $\mathbf{A}\mathbf{v}_1$ y $\mathbf{B}\mathbf{v}_2$ al grupo de vectores bajo la suma:
+
+$$
+\begin{align*}
+\mathbf{A} &= \begin{bmatrix}
+6 \\
+4 \\
+\end{bmatrix}
+,
+\begin{bmatrix}
+3 \\
+7 \\
+\end{bmatrix}\\
+\mathbf{B} &= \begin{bmatrix}
+3 \\
+12 \\
+\end{bmatrix}
+,
+\begin{bmatrix}
+9 \\
+6 \\
+\end{bmatrix}
+\end{align*}
+$$
+
+Ahora queremos encontrar el equivalente homomórfico de
+
+$$
+\begin{bmatrix}
+6 \\
+4 \\
+\end{bmatrix}\cdot 2+
+\begin{bmatrix}
+3 \\
+7 \\
+\end{bmatrix}\cdot 4\stackrel{?}{=}
+\begin{bmatrix}
+3 \\
+12 \\
+\end{bmatrix}\cdot 2=
+\begin{bmatrix}
+9 \\
+6 \\
+\end{bmatrix}\cdot 2
+$$
+
+en el grupo de polinomios.
+
+Convirtamos cada uno de los vectores en polinomios sobre los valores $x$ $[1,2]$:
+
+$$
+\underbrace{
+\begin{bmatrix}
+6 \\
+4 \\
+\end{bmatrix}}_{p_1(x)}\cdot 2+
+\underbrace{
+\begin{bmatrix}
+3 \\
+7 \\
+\end{bmatrix}}_{p_2(x)}\cdot 4\stackrel{?}{=}
+\underbrace{
+\begin{bmatrix}
+3 \\
+12 \\
+\end{bmatrix}}_{q_1(x)}\cdot 2=
+\underbrace{
+\begin{bmatrix}
+9 \\
+6 \\
+\end{bmatrix}}_{q_2(x)}\cdot 2
+$$
+
+Invocaremos algo de Python para calcular la interpolación de Langrage:
+
+```python
+import galois
+import numpy as np
+
+p = 17
+GF = galois.GF(p)
+
+x_values = GF(np.array([1, 2]))
+
+def L(v):
+ return galois.lagrange_poly(x_values, v)
+
+p1 = L(GF(np.array([6, 4])))
+p2 = L(GF(np.array([3, 7])))
+q1 = L(GF(np.array([3, 12])))
+q2 = L(GF(np.array([9, 6])))
+
+print(p1)
+# 15x + 8 (mod 17)
+print(p2)
+# 4x + 16 (mod 17)
+print(q1)
+# 9x + 11 (mod 17)
+print(q2)
+# 14x + 12 (mod 17)
+```
+
+Finalmente, podemos comprobar si
+
+$$p_1(x) \cdot 2+ p_2(x) \cdot 4 \stackrel{?}= q_1(x) \cdot 2 + q_2(x) \cdot 2$$
+
+es verdadero invocando el Lemma de Schwartz-Zippel:
+
+```python
+import random
+u = random.randint(0, p)
+tau = GF(u) # un punto aleatorio
+
+left_hand_side = p1(tau) * GF(2) + p2(tau) * GF(4)
+right_hand_side = q1(tau) * GF(2) + q2(tau) * GF(2)
+
+assert left_hand_side == right_hand_side
+```
+
+**La declaración assert final puede probar si $\mathbf{A}\mathbf{v}_1 = \mathbf{B}\mathbf{v}_2$ haciendo una sola comparación en lugar de $n$.**
+
+## R1CS a QAP: Probar sucintamente que $\mathbf{L}\mathbf{a}\circ\mathbf{R}\mathbf{a}=\mathbf{O}\mathbf{a}$
+Dado que sabemos cómo probar $\mathbf{A}\mathbf{v}_1 = \mathbf{B}\mathbf{v}_2$ sucintamente, ¿podemos también probar si $\mathbf{L}\mathbf{a}\circ\mathbf{R}\mathbf{a}=\mathbf{O}\mathbf{a}$ de manera sucinta?
+
+Las matrices tienen $m$ columnas, así que vamos a dividir cada una de las matrices en $m$ vectores columna e interpolarlos en $(1, 2, ..., n)$ para producir $m$ polinomios cada uno.
+
+Sean $u_1(x), u_2(x), ..., u_m(x)$ los polinomios que interpolan los vectores columna de $\mathbf{L}$.
+
+Sean $v_1(x), v_2(x), ..., v_m(x)$ los polinomios que interpolan los vectores columna de $\mathbf{R}$.
+
+Sean $w_1(x), w_2(x), ..., w_m(x)$ los polinomios que interpolan los vectores columna de $\mathbf{O}$.
+
+Sin pérdida de generalidad, digamos que tenemos 4 columnas ($m = 4$) y tres filas ($n = 3$).
+
+Visualmente, esto se puede representar como
+$$
+\begin{array}{c}
+\mathbf{L} = \begin{bmatrix}
+\quad l_{11} \quad& l_{12} \quad& l_{13} \quad& l_{14} \quad\\
+\quad l_{21} \quad& l_{22} \quad& l_{23} \quad& l_{24} \quad\\
+\quad l_{31} \quad& l_{32} \quad& l_{33} \quad& l_{34} \quad
+\end{bmatrix} \\
+\\
+\qquad u_1(x) \quad u_2(x) \quad u_3(x) \quad u_4(x)
+\end{array}
+\begin{array}{c}
+\mathbf{R} = \begin{bmatrix}
+\quad r_{11} \quad& r_{12} \quad& r_{13} \quad& r_{14} \quad\\
+\quad r_{21} \quad& r_{22} \quad& r_{23} \quad& r_{24} \quad\\
+\quad r_{31} \quad& r_{32} \quad& r_{33} \quad& r_{34} \quad
+\end{bmatrix} \\
+\\
+\qquad v_1(x) \quad v_2(x) \quad v_3(x) \quad v_4(x)
+\end{array}
+$$
+
+$$
+\begin{array}{c}
+\mathbf{O} = \begin{bmatrix}
+\quad o_{11} \quad& o_{12} \quad& o_{13} \quad& o_{14} \quad\\
+\quad o_{21} \quad& o_{22} \quad& o_{23} \quad& o_{24} \quad\\
+\quad o_{31} \quad& o_{32} \quad& o_{33} \quad& o_{34} \quad
+\end{bmatrix} \\
+\\
+\qquad w_1(x) \quad w_2(x) \quad w_3(x) \quad w_4(x)
+\end{array}
+$$
+
+Dado que multiplicar un vector columna por un escalar es homomórfico a multiplicar un polinomio por un escalar, cada uno de los polinomios se puede multiplicar por el elemento respectivo en el testigo.
+
+Por ejemplo,
+
+$$
+\mathbf{L}\mathbf{a} = \begin{bmatrix}
+\quad l_{11} \quad& l_{12} \quad& l_{13} \quad& l_{14} \quad\\
+\quad l_{21} \quad& l_{22} \quad& l_{23} \quad& l_{24} \quad\\
+\quad l_{31} \quad& l_{32} \quad& l_{33} \quad& l_{34} \quad
+\end{bmatrix}
+\begin{bmatrix}
+a_1 \\
+a_2 \\
+a_3 \\
+a_4
+\end{bmatrix}
+$$
+
+se convierte en
+
+$$
+\begin{align*}
+&=\begin{bmatrix}
+u_1(x) & u_2(x) & u_3(x) & u_4(x)
+\end{bmatrix}
+\begin{bmatrix}
+a_1 \\
+a_2 \\
+a_3 \\
+a_4
+\end{bmatrix}\\
+&=a_1u_1(x) + a_2u_2(x) + a_3u_3(x) + a_4u_4(x)\\
+&=\sum_{i=1}^4 a_iu_i(x)
+\end{align*}
+$$
+
+Observe que el resultado final es un único polinomio con grado como máximo $n - 1$ (ya que hay $n$ filas en $\mathbf{L}$, $u_1(x), ..., u_n(x)$ tienen grado como máximo $n - 1$).
+
+En el caso general, $\mathbf{L}\mathbf{a}$ se puede escribir como
+
+$$
+\sum_{i=1}^m a_iu_i(x)
+$$
+
+después de convertir cada una de las $m$ columnas en polinomios.
+
+Usando los mismos pasos anteriores, cada producto de matriz testigo en el R1CS $\mathbf{L}\mathbf{a}\circ\mathbf{R}\mathbf{a} = \mathbf{O}\mathbf{a}$ se puede transformar como
+
+$$
+\begin{align*}
+\mathbf{L}\mathbf{a} \rightarrow \sum_{i=1}^m a_iu_i(x) \\
+\mathbf{R}\mathbf{a} \rightarrow \sum_{i=1}^m a_iv_i(x) \\
+\mathbf{O}\mathbf{a} \rightarrow \sum_{i=1}^m a_iw_i(x)
+\end{align*}
+$$
+
+Dado que cada uno de los términos de suma produce un solo polinomio, podemos escribirlos como:
+
+$$
+\begin{align*}
+\mathbf{L}\mathbf{a} &\rightarrow \sum_{i=1}^m a_iu_i(x) = u(x)\\
+\mathbf{R}\mathbf{a} &\rightarrow \sum_{i=1}^m a_iv_i(x) = v(x)\\
+\mathbf{O}\mathbf{a} &\rightarrow \sum_{i=1}^m a_iw_i(x) = w(x)
+\end{align*}
+$$
+
+### ¿Por qué interpolar todas las columnas?
+Debido a los homomorfismos $\mathcal{L}(\mathbf{v}_1) + \mathcal{L}(\mathbf{v}_2) = \mathcal{L}(\mathbf{v}_1 + \mathbf{v}_2)$ y $\mathcal{L}(\lambda \mathbf{v}) = \lambda \mathcal{L}(\mathbf{v})$, si calculamos $u(x)$ como $\mathcal{L}(\mathbf{L}\mathbf{a})$ obtenemos el mismo resultado que si aplicamos la interpolación de Lagrange a las columnas de $\mathbf{L}$ y luego multiplicamos cada uno de los polinomios por el elemento respectivo en $\mathbf{a}$ y sumamos el resultado.
+
+Dicho de otra manera,
+
+$$
+\sum_{i=1}^m a_iu_i(x) = \mathcal{L}(\mathbf{L}\mathbf{a}) \mid u_i(x) \text{ es la interpolación de Lagrange de la columna } i \text{ de } \mathbf{L}
+$$
+
+Entonces, ¿por qué no calcular una única interpolación de Lagrange en lugar de $m$?
+
+Necesitamos hacer una distinción entre *quién* está usando el QAP. El verificador (y la configuración confiable que veremos más adelante) no conocen al testigo $\mathbf{a}$ y, por lo tanto, no pueden calcular $\mathcal{L}(\mathbf{L}\mathbf{a})$. Esta es una optimización que puede hacer el probador, pero otras partes en el protocolo ZK no pueden hacer uso de esa optimización.
+
+Todas las partes involucradas deben tener un acuerdo común sobre el QAP (las interpolaciones polinómicas de las matrices) antes de que se realicen las pruebas y verificaciones.
+
+### Desequilibrio de grado polinómico
+
+Sin embargo, no podemos expresar simplemente el resultado final como
+
+$$u(x)v(x) = w(x)$$
+
+porque los grados no coincidirán.
+
+La multiplicación de dos polinomios da como resultado un polinomio producto cuyo grado es la suma de los grados de los dos polinomios que se multiplican.
+
+Como cada uno de $u(x)$, $v(x)$ y $w(x)$ tendrá grado $n - 1$, $u(x)v(x)$ generalmente tendrá grado $2n - 2$ y $w(x)$ tendrá grado $n - 1$, por lo que no serán iguales aunque los vectores subyacentes que multiplicaron sean iguales.
+
+Esto se debe a que los homomorfismos que establecimos anteriormente solo hacen afirmaciones sobre la suma de vectores, no sobre el producto de Hadamard.
+
+Sin embargo, el vector que $u(x)v(x)$ interpola, es decir,
+
+$$((1, u(1)v(1)), (2, u(2)v(2)), ..., (n, u(n)v(n)))$$
+
+es el mismo que el vector que $w(x)$ interpola, es decir,
+
+$$((1, w(1)), \quad (2, w(2)), \quad ..., \quad (n, w(n)))$$
+
+En otras palabras
+
+$$((1, u(1)v(1)), (2, u(2)v(2)), ..., (n, u(n)v(n))) = ((1, w(1)), (2, w(2)), ..., (n, w(n)))$$
+
+Aunque los vectores "subyacentes" son iguales, los polinomios que los interpolan no son iguales.
+
+### Ejemplo de igualdad subyacente
+Digamos que $u(x)$ es el polinomio que interpola
+
+$$(1,\boxed{2}), (2,\boxed{4}), (3,\boxed{8})$$
+
+y $v(x)$ es el polinomio que interpola
+
+$$(1,\boxed{4}), (2,\boxed{2}), (3,\boxed{8})$$
+
+Si tratamos a $u(x)$ como interpolando el vector $[2,4,8]$ y a $v(x)$ como interpolando el vector $[4,2,8]$, entonces podemos ver que su polinomio producto interpola el producto Hadamard de los dos vectores. El producto Hadamard de $[2,4,8]$ y $[4,2,8]$ es $[8,8,64]$.
+
+Si multiplicamos $u(x)$ y $v(x)$, obtenemos $w(x) = 4x^4 - 18x^3 + 36x^2 - 42x + 28$.
+
+Podemos ver en el gráfico a continuación que el polinomio producto interpola el producto de Hadamard $[8, 8, 64]$ de los dos vectores.
+
+
+
+Entonces, ¿cómo podemos "hacer" que $w(x)$ sea igual a $u(x)v(x)$ si interpolan los mismos valores de $y$ sobre $(1,2,...,n)$?
+
+### Interpolación del vector $\mathbf{0}$
+Si $\mathbf{v_1} \circ \mathbf{v_2} = \mathbf{v_3}$, entonces $\mathbf{v_1} \circ \mathbf{v_2} = \mathbf{v_3} + \mathbf{0}$.
+
+En lugar de interpolar $\mathbf{0}$ con la interpolación de Lagrange y obtener $f(x) = 0$ (recuerde que la interpolación de Lagrange encuentra el polinomio de interpolación de grado más bajo), podemos usar un polinomio de grado más alto que equilibrará la discrepancia en grados.
+
+Por ejemplo, el polinomio negro ($b(x)$) en la imagen de abajo interpola $[(1,0), (2,0), (3,0)]$:
+
+
+
+Ahora, dado que $4x^4 -18x^3 + 8x^2 + 42x - 36$ es una interpolación válida de $[0,0,0]$, podemos escribir nuestra ecuación original
+
+$u(x)v(x) = w(x) + b(x)$
+
+¡y la ecuación estará balanceada!
+
+$b(x)$ se calculó simplemente como $u(x)v(x) - w(x)$ (el polinomio azul menos el polinomio rojo)
+
+Sin embargo, no podemos dejar que el probador elija *cualquier* $b(x)$, de lo contrario podría elegir un $b(x)$ que equilibre $u(x)v(x)$ y $w(x)$ incluso si no interpola el mismo vector ($[8, 8, 64]$ en nuestro ejemplo). El probador tiene demasiada flexibilidad para elegir $b(x)$. Específicamente, queremos exigir que $b(x)$ tenga raíces en $x = 1,2,\dots,n$, es decir, que interpole el vector $\mathbf{0}$. De esa manera, la transformación polinómica de $\mathbf{v}_1 \circ \mathbf{v}_2 = \mathbf{v}_3 + \mathbf{0}$ aún respeta los vectores subyacentes.
+
+Para restringir su elección de $b(x)$, podemos usar el siguiente teorema:
+
+#### La unión de raíces del producto polinómico
+**Teorema**: Si $h(x) = f(x)g(x)$ y $f(x)$ tiene un conjunto de raíces $\set{r_f}$ y $g(x)$ tiene un conjunto de raíces $\set{r_g}$, entonces $h(x)$ tiene raíces $\set{r_f} \cup \set{r_g}$.
+
+##### Ejemplo
+Sea $f(x) = (x - 3)(x - 4)$ y $g(x) = (x - 5)(x - 6)$. Entonces $h(x) = f(x)g(x)$ tiene raíces $\set{3,4,5,6}$.
+
+Podemos usar el teorema anterior para hacer cumplir que $b(x)$ tiene raíces en $x = 1,2,\dots,n$.
+
+#### Forzando a $b(x)$ a ser el vector cero
+Descomponemos $b(x)$ en $b(x) = h(x)t(x)$ donde $t(x)$ es el polinomio
+
+$$
+t(x) = (x-1)(x-2)\dots(x-n)
+$$
+
+entonces cualquier polinomio multiplicado por $t(x)$ también será el vector cero, ya que debe tener raíces en $x = 1,2,\dots,n$.
+
+Por lo tanto, reemplazaremos $b(x)$ con $h(x)t(x)$ en nuestra ecuación.
+
+Por lo tanto, nuestra igualdad se convertirá en
+
+$$
+u(x)v(x) = w(x) + h(x)t(x)
+$$
+
+Podemos calcular $h(x)$ usando álgebra básica:
+
+$$
+h(x) = \frac{u(x)v(x) - w(x)}{t(x)}
+$$
+
+## QAP de extremo a extremo
+Supongamos que tenemos un R1CS con matrices $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$ y el vector testigo $\mathbf{a}$.
+
+$$\mathbf{L}\mathbf{a}\circ\mathbf{R}\mathbf{a} = \mathbf{O}\mathbf{a}$$
+
+Las matrices tienen $n$ columnas y $m$ filas donde $n = 3$ y $m = 4$.
+
+Es decir, $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$ son los siguientes:
+
+$$
+\begin{array}{c}
+\mathbf{L} = \begin{bmatrix}
+\quad l_{11} \quad& l_{12} \quad& l_{13} \quad& l_{14} \quad\\
+\quad l_{21} \quad& l_{22} \quad& l_{23} \quad& l_{24} \quad\\
+\quad l_{31} \quad& l_{32} \quad& l_{33} \quad& l_{34} \quad
+\end{bmatrix} \\
+\\
+\mathbf{R} = \begin{bmatrix}
+\quad r_{11} \quad& r_{12} \quad& r_{13} \quad& r_{14} \quad\\
+\quad r_{21} \quad& r_{22} \quad& r_{23} \quad& r_{24} \quad\\
+\quad r_{31} \quad& r_{32} \quad& r_{33} \quad& r_{34} \quad
+\end{bmatrix} \\
+\\
+\mathbf{O} = \begin{bmatrix}
+\quad o_{11} \quad& o_{12} \quad& o_{13} \quad& o_{14} \quad\\
+\quad o_{21} \quad& o_{22} \quad& o_{23} \quad& o_{24} \quad\\
+\quad o_{31} \quad& o_{32} \quad& o_{33} \quad& o_{34} \quad
+\end{bmatrix}
+\end{array}
+$$
+
+Y el vector testigo $\mathbf{a}$ es
+
+$$\mathbf{a} = \begin{bmatrix}
+a_1 \\ a_2 \\ a_3 \\ a_4
+\end{bmatrix}$$
+
+Dividimos cada una de las matrices en $m$ vectores columna y los interpolamos en $(1, 2, ..., n)$ para producir $m$ polinomios cada uno.
+
+$$
+\begin{array}{c}
+\mathbf{L} = \underbrace{\begin{bmatrix}
+l_{11} \\l_{12} \\ l_{13} \\ l_{14} \\
+\end{bmatrix}}_{u_1(x)}
+\quad
+\underbrace{\begin{bmatrix}
+l_{21} \\ l_{22} \\ l_{23} \\ l_{24}
+\end{bmatrix}}_{u_2(x)}
+\quad
+\underbrace{\begin{bmatrix}
+l_{31} \\ l_{32} \\ l_{33} \\ l_{34} \\
+\end{bmatrix}}_{u_3(x)}
+\quad
+\underbrace{\begin{bmatrix}
+l_{41} \\ l_{42} \\ l_{43} \\ l_{44}
+\end{bmatrix}}_{u_4(x)}
+\end{array}
+$$
+
+$$
+\begin{array}{c}
+\mathbf{R} = \underbrace{\begin{bmatrix}
+r_{11} \\r_{12} \\ r_{13} \\ r_{14} \\
+\end{bmatrix}}_{v_1(x)}
+\quad
+\underbrace{\begin{bmatrix}
+r_{21} \\ r_{22} \\ r_{23} \\ r_{24}
+\end{bmatrix}}_{v_2(x)}
+\quad
+\underbrace{\begin{bmatrix}
+r_{31} \\ r_{32} \\ r_{33} \\ r_{34} \\
+\end{bmatrix}}_{v_3(x)}
+\quad
+\underbrace{\begin{bmatrix}
+r_{41} \\ r_{42} \\ r_{43} \\ r_{44}
+\end{bmatrix}}_{v_4(x)}
+\end{array}
+$$
+
+$$
+\begin{array}{c}
+\mathbf{O} = \underbrace{\begin{bmatrix}
+o_{11} \\o_{12} \\ o_{13} \\ o_{14} \\
+\end{bmatrix}}_{w_1(x)}
+\quad
+\underbrace{\begin{bmatrix}
+o_{21} \\ o_{22} \\ o_{23} \\ o_{24}
+\end{bmatrix}}_{w_2(x)}
+\quad
+\underbrace{\begin{bmatrix}
+o_{31} \\ o_{32} \\ o_{33} \\ o_{34} \\
+\end{bmatrix}}_{w_3(x)}
+\quad
+\underbrace{\begin{bmatrix}
+o_{41} \\ o_{42} \\ o_{43} \\ o_{44}
+\end{bmatrix}}_{w_4(x)}
+\end{array}
+$$
+
+Cada uno de los productos matriz-vector $\mathbf{L}\mathbf{a}$, $\mathbf{R}\mathbf{a}$ y $\mathbf{O}\mathbf{a}$ son homomórficamente equivalentes de la siguiente manera polinomios:
+
+$$
+\begin{align*}
+\sum_{i=1}^4 a_iu_i(x) &= a_1u_1(x) + a_2u_2(x) + a_3u_3(x) + a_4u_4(x) = u(x) \\
+\sum_{i=1}^m a_iv_i(x) &= a_1v_1(x) + a_2v_2(x) + a_3v_3(x) + a_4v_4(x) = v(x) \\
+\sum_{i=1}^m a_iw_i(x) &= a_1w_1(x) + a_2w_2(x) + a_3w_3(x) + a_4w_4(x) = w(x) \\
+\end{align*}
+$$
+
+En nuestro caso, $t(x)$ será
+
+$$t(x) = (x - 1)(x - 2)(x - 3)$$
+
+y $h(x)$ será
+
+$$h(x) = \frac{u(x)v(x) - w(x)}{t(x)}$$
+
+La fórmula final para una representación QAP del R1CS original es
+
+$$\sum_{i=1}^4 a_iu_i(x)\sum_{i=1}^4 a_iv_i(x) = \sum_{i=1}^4 a_iw_i(x) + h(x)t(x)$$
+
+## Fórmula final para un QAP
+Un QAP es la siguiente fórmula:
+
+$$\sum_{i=1}^m a_iu_i(x)\sum_{i=1}^m a_iv_i(x) = \sum_{i=1}^m a_iw_i(x) + h(x)t(x)$$
+
+Donde $u_i(x)$, $v_i(x)$ y $w_i(x)$ son polinomios que interpolan las columnas de $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$ respectivamente, $t(x)$ es $(x - 1)(x - 2)...(x - n)$, donde $n$ es el número de filas en $\mathbf{L}$, $\mathbf{R}$ y $\mathbf{O}$, y $h(x)$ es
+
+$$
+h(x) = \frac{\sum_{i=1}^ma_iu_i(x)\sum_{i=1}^ma_iv_i(x) - \sum_{i=1}^ma_iw_i(x)}{t(x)}
+$$
+
+## Zero Knowledge Proofs suscinto con programas de Aritmética Cuadrática
+Supongamos que tuviéramos una forma para que el verificador envíe un valor aleatorio $\tau$ al probador y que este respondiera con
+
+$$
+\begin{align*}
+A &= u(\tau)\\
+B &= v(\tau)\\
+C &= w(\tau) + h(\tau)t(\tau)
+\end{align*}
+$$
+
+El verificador podría verificar que $AB = C$ y aceptar que el probador tiene un testigo válido $\mathbf{a}$ que satisface tanto el R1CS como el QAP.
+
+Sin embargo, esto requeriría que el verificador confíe en que el probador está evaluando los polinomios correctamente, y no tenemos un mecanismo para obligar al probador a hacerlo.
+
+En el próximo capítulo, mostraremos el código Python para [convertir un R1CS en un QAP](https://www.rareskills.io/post/r1cs-to-qap) según lo que analizamos en este capítulo.
+
+Luego, analizaremos las configuraciones confiables para comenzar a abordar el problema de cómo lograr que el demostrador evalúe los polinomios de manera honesta.
+
+*Traducido al Español por **ARCADIO Garcia**, Septiembre 2024*
\ No newline at end of file