Skip to content
New issue

Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.

Sign up for GitHub

By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.

Already on GitHub? Sign in to your account

Jump to bottom

Riemannian SVRG: Fast Stochastic Optimization on Riemannian Manifolds #6

Open
nocotan opened this issue Dec 30, 2020 · 0 comments
Open

Riemannian SVRG: Fast Stochastic Optimization on Riemannian Manifolds #6

nocotan opened this issue Dec 30, 2020 · 0 comments
Assignees
@nocotan
Labels
riemannian optimization

Comments

@nocotan
Copy link
Member

nocotan commented Dec 30, 2020

一言でいうと

分散緩和のリーマン確率的最適化の手法であるRiemannian SVRG (RSVRG)を提案．

論文リンク

NeurIPS2016:
https://papers.nips.cc/paper/2016/file/98e6f17209029f4ae6dc9d88ec8eac2c-Paper.pdf

著者/所属機関

Hongyi Zhang (MIT), Sashank J. Reddi (Carnegie Mellon University), Suvrit Sra (MIT)

投稿日付(yyyy/MM/dd)

2016/05/23

概要

以下のようなリーマン多様体(M,g)の上の有限和最適化問題を扱う．
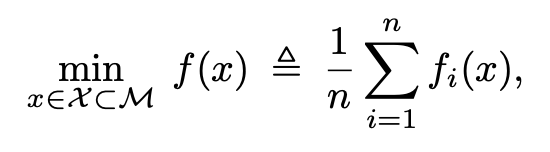
Screen Shot 2020-12-30 at 23 18 07

この問題について，分散緩和のリーマン確率的最適化の手法であるRiemannian SVRG (RSVRG)を提案．

Screen Shot 2020-12-30 at 23 30 41

新規性・差分

測地的強凸な関数の大域的線形収束レートと、測地的非凸な最適化のための一次非漸近収束レートを備えた最初の確率的勾配法を提案

手法

Screen Shot 2020-12-30 at 23 31 14

Screen Shot 2020-12-30 at 23 31 35

結果

Screen Shot 2020-12-30 at 23 32 22

Screen Shot 2020-12-30 at 23 32 42

コメント
Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment
Assignees

@nocotan nocotan

Labels
riemannian optimization
Projects
None yet
Milestone
No milestone
Development

No branches or pull requests
1 participant
@nocotan